A Geometria Espacial costuma assustar muitos estudantes, mas a verdade é que ela se torna simples quando você organiza as fórmulas, visualiza as figuras e entende como cada volume ou área nasce das medidas essenciais. Neste artigo, vamos caminhar juntos por cubos, cones, cilindros, paralelepípedos e até pela relação de Euler, sempre com linguagem clara, exemplos resolvidos e exercícios com sistema abre e fecha. Com isso, você terá nos seus dedos tudo o que precisa para mandar bem em provas de concursos, ENEM, vestibulares e até na sala de aula.
Relação de Euler e propriedades essenciais das figuras 3D
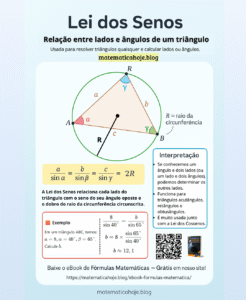
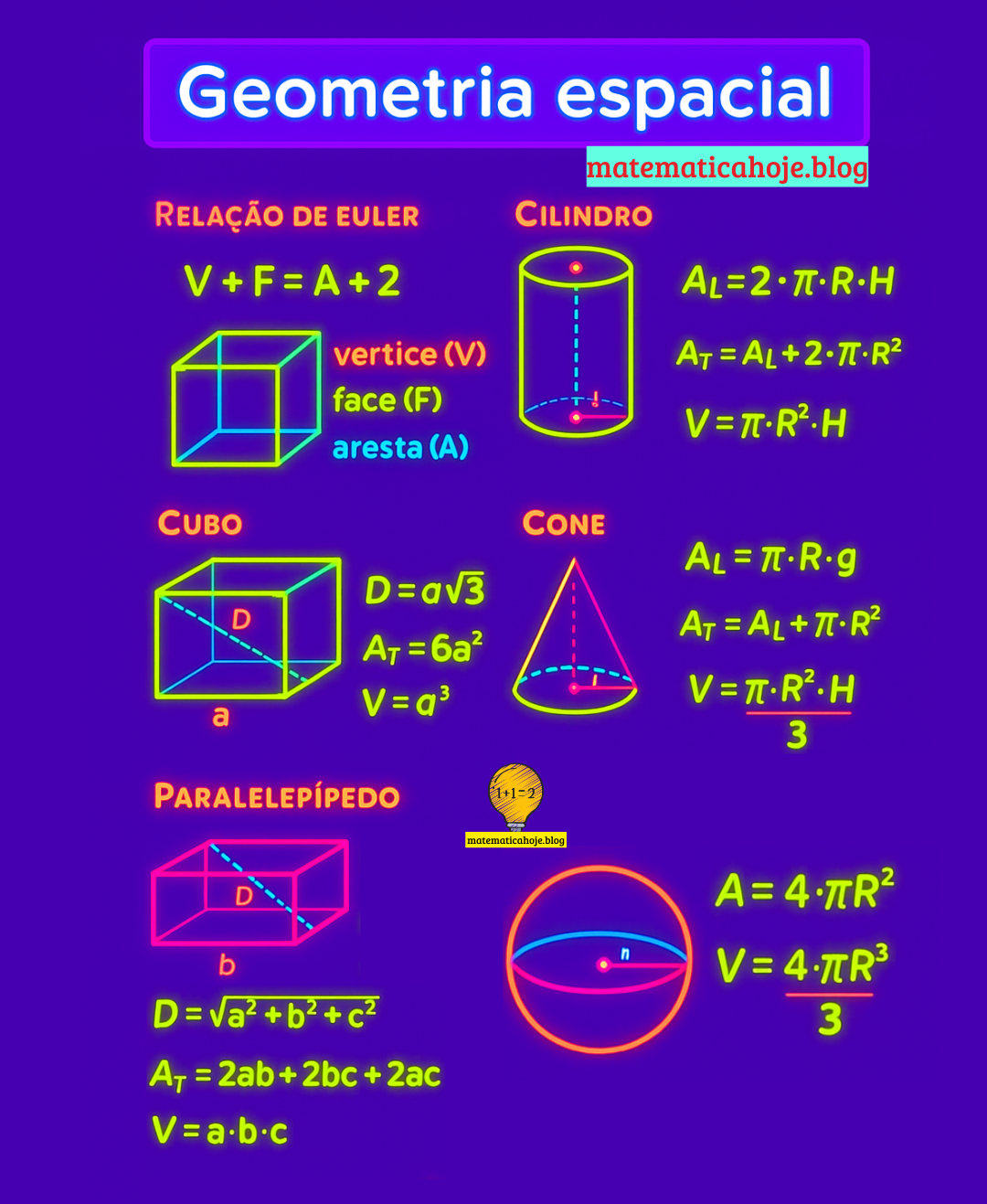
A Relação de Euler é uma das portas de entrada para entender poliedros:
\[ V + F = A + 2 \]Onde: • \(V\): vértices • \(F\): faces • \(A\): arestas
Exemplo prático: cubo
Um cubo tem: \(V = 8\), \(F = 6\), \(A = 12\)
Aplicando Euler: \[ 8 + 6 = 12 + 2 \] \[ 14 = 14 \]
Fórmulas principais para cubo e paralelepípedo
Cubo: área, diagonal e volume
\[ D = a\sqrt{3} \] \[ A_T = 6a^2 \] \[ V = a^3 \]Exemplo rápido
Calcule o volume de um cubo com aresta \(a = 5\).
\[ V = a^3 \] \[ V = 5^3 \] \[ V = 125 \]—Paralelepípedo: diagonal, área total e volume
\[ D = \sqrt{a^2 + b^2 + c^2} \] \[ A_T = 2ab + 2bc + 2ac \] \[ V = a \cdot b \cdot c \]Exemplo prático
Um paralelepípedo possui \(a=3\), \(b=4\), \(c=5\). Encontre o volume:
\[ V = a \cdot b \cdot c \] \[ V = 3 \cdot 4 \cdot 5 \] \[ V = 60 \]—Cilindro e Cone: áreas e volumes explicados
Cilindro
\[ A_L = 2\pi R H \] \[ A_T = A_L + 2\pi R^2 \] \[ V = \pi R^2 H \]Exemplo
Calcule o volume de um cilindro com \(R=3\) e \(H=10\):
\[ V = \pi R^2 H \] \[ V = \pi \cdot 3^2 \cdot 10 \] \[ V = 90\pi \]—Cone
\[ A_L = \pi R g \] \[ A_T = A_L + \pi R^2 \] \[ V = \frac{\pi R^2 H}{3} \]—Esfera: fórmula da área e do volume
\[ A = 4\pi R^2 \] \[ V = \frac{4\pi R^3}{3} \]——Lista de Exercícios com Soluções Passo a Passo
Questão 1
Um cubo possui aresta de 6 cm. Qual seu volume?
Questão 2
Calcule o volume de um cilindro com \(R = 4\) e \(H = 5\).
Questão 3
Qual a diagonal de um paralelepípedo com \(a=2\), \(b=3\), \(c=6\)?
Conclusão
A Geometria Espacial se torna simples quando você organiza as fórmulas e entende como cada figura se comporta. Com os exemplos, exercícios interativos e links complementares deste artigo, você já tem um caminho completo para dominar cubo, cilindro, cone, esfera e paralelepípedo. Continue estudando com mapas mentais, listas de exercícios e o eBook gratuito de fórmulas para fechar o conteúdo.
—FAQ – Perguntas Frequentes
Como memorizar fórmulas de Geometria Espacial rapidamente?
A melhor estratégia é visualizar as figuras e praticar exercícios que relacionem medidas de área e volume. Usar mapas mentais e revisões espaçadas reforça os conceitos sem esforço.
Quais figuras mais caem no ENEM?
O ENEM prioriza cilindro, cone e esfera, especialmente em problemas de aplicação prática envolvendo áreas e volumes. Também aparecem questões com interpretação gráfica e proporcionalidade.
Como saber quando usar área lateral ou total?
A questão sempre indica: se envolver pintura, contato externo ou revestimento, use área total. Se envolver apenas o “corpo” da figura, sem tampas, use área lateral.
É possível estudar Geometria Espacial do zero?
Sim. Comece pelos sólidos mais simples, entenda cada fórmula e pratique com problemas progressivos. Mapas mentais e exercícios comentados aceleram o aprendizado.
Autor: Adriano Rocha