Domine o tema “Figuras Semelhantes” com esta seleção de 6 questões resolvidas de forma clara, didática e visual. Cada exercício conta com imagem, explicações detalhadas, uso de linguagem matemática com MathJax e sistema de abre e fecha para facilitar seu estudo. Ideal para alunos do ensino fundamental, médio, Enem e preparatórios para concursos. No final de cada questão, aproveite os eBooks gratuitos e mapas mentais para revisar com mais eficiência!
Exercício Figuras Semelhantes
Questão 1
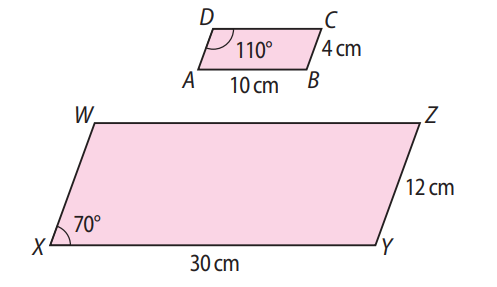
Verifique se os paralelogramos ABCD e XYZW são semelhantes.
São semelhantes.
🔍 Passo a passo:
1) Comparação dos ângulos:
- Paralelogramo ABCD: apresenta um ângulo interno de 110°. Logo, o ângulo adjacente mede 70°, pois são suplementares.
- Paralelogramo XYZW: apresenta um ângulo de 70° e, portanto, também possui um ângulo de 110°.
✅ Todos os ângulos correspondentes são congruentes.
2) Comparação dos lados correspondentes:
- AB = 10 cm e XY = 30 cm → razão = 10/30 = 1/3
- BC = 4 cm e YZ = 12 cm → razão = 4/12 = 1/3
✅ Os lados correspondentes também são proporcionais.
3) Conclusão:
- Seus ângulos correspondentes são congruentes (110° e 70°);
- Seus lados correspondentes são proporcionais com razão de semelhança 1/3.
📚 Continue estudando com nossos materiais gratuitos:
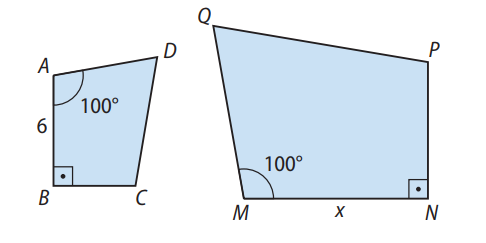
Os quadriláteros ABCD e MNPQ a seguir são semelhantes, e o lado AB do primeiro corresponde ao lado MN do segundo. Se a razão de semelhança do quadrilátero ABCD para o quadrilátero MNPQ é de \( \dfrac{3}{5} \), determine a medida do lado MN do quadrilátero MNPQ.
🔍 Passo a passo:
1) Dados do problema:
- \( AB = 6 \, \text{cm} \)
- \( MN = x \)
- Razão de semelhança: \( \dfrac{AB}{MN} = \dfrac{3}{5} \)
2) Estabelecendo a proporção:
\( \dfrac{6}{x} = \dfrac{3}{5} \)
3) Resolvendo a equação (produto cruzado):
\( 3x = 6 \cdot 5 \)
\( 3x = 30 \)
\( x = \dfrac{30}{3} = 10 \)
✅ Portanto, a medida do lado \( MN \) é 10 cm.
📚 Continue estudando com nossos materiais gratuitos:
Sobre polígonos semelhantes e congruentes, é correto afirmar que:
a) se as medidas dos lados de um dos polígonos são iguais às medidas dos lados do outro, eles são congruentes. b) dois polígonos com número de lados diferentes podem ser semelhantes. c) dois polígonos semelhantes são sempre congruentes. d) dois polígonos congruentes são sempre semelhantes. e) dois polígonos são semelhantes se as somas das medidas dos ângulos internos desses polígonos são iguais.🔍 Análise das alternativas:
Alternativa a) ❌ Incorreta., pois se os lados e ângulos são iguais, os polígonos são congruentes. Mas atenção: a congruência exige também os ângulos congruentes — aqui, foi omitido.
Alternativa b) ❌ Incorreta. Polígonos só podem ser semelhantes se tiverem o mesmo número de lados.
Alternativa c) ❌ Incorreta. Polígonos semelhantes têm lados proporcionais e ângulos congruentes, mas não são necessariamente congruentes (congruência exige mesma medida).
Alternativa d) ✅ Correta. Se dois polígonos são congruentes, então eles têm lados iguais e ângulos iguais — portanto, também são semelhantes (pois lados iguais ⇒ proporcionais).
Alternativa e) ❌ Errada. A soma dos ângulos internos de um polígono depende do número de lados, não é critério de semelhança.
Dois polígonos congruentes são sempre semelhantes, pois a congruência é um caso particular da semelhança (razão de semelhança = 1).
📚 Continue estudando com nossos materiais gratuitos:
A razão de semelhança entre dois decágonos regulares é \( \dfrac{3}{5} \). Se o perímetro do decágono que possui o maior lado é 720 mm, qual é a medida do lado, em centímetros, do outro decágono?
🔍 Passo a passo:
1) Dados importantes:
- Razão de semelhança: \( \dfrac{3}{5} \)
- Perímetro do maior decágono: 720 mm
- Decágono: possui 10 lados
2) Calculando a medida do lado do maior decágono:
\[ \text{Lado maior} = \frac{720}{10} = 72 \, \text{mm} \]
3) Aplicando a razão de semelhança:
\[ \text{Lado menor} = 72 \cdot \frac{3}{5} = \frac{216}{5} = 43{,}2 \, \text{mm} \]
4) Convertendo para centímetros:
\[ 43{,}2 \, \text{mm} = 4{,}32 \, \text{cm} \]
✅ Resposta final: A medida do lado do outro decágono é 4,32 cm.
📚 Continue estudando com nossos materiais gratuitos:
Os tampos de duas mesas retangulares são semelhantes. A razão de semelhança entre as medidas dos lados da maior para a menor é 1,5. Se as dimensões do tampo da mesa menor são 3,5 m e 2,5 m, determine o perímetro do tampo da mesa maior.
🔍 Passo a passo:
1) Dados do problema:
- Razão de semelhança (maior/menor): \( 1{,}5 \)
- Dimensões da mesa menor: \( 3{,}5\, \text{m} \) e \( 2{,}5\, \text{m} \)
2) Calculando as dimensões da mesa maior:
\[ 3{,}5 \times 1{,}5 = 5{,}25\, \text{m} \quad \text{e} \quad 2{,}5 \times 1{,}5 = 3{,}75\, \text{m} \]
3) Calculando o perímetro da mesa maior:
\[ P = 2 \cdot (5{,}25 + 3{,}75) = 2 \cdot 9 = 18\, \text{m} \]
✅ Resposta final: O perímetro do tampo da mesa maior é 18 metros.
📚 Continue estudando com nossos materiais gratuitos:
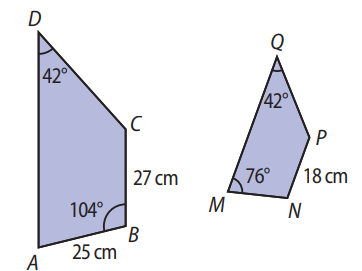
Os trapézios ABCD e MNPQ representados a seguir são semelhantes.
🔍 Análise dos trapézios semelhantes:
Sabemos que os trapézios ABCD e MNPQ são semelhantes. Isso significa que:
- Seus ângulos correspondentes são iguais;
- Seus lados correspondentes são proporcionais.
Ângulos correspondentes:
- \( \angle D = \angle Q = 42^\circ \)
- \( \angle B = \angle N = 104^\circ \)
Lados conhecidos:
- Base menor do trapézio maior: \( AB = 25\,\text{cm} \)
- Altura do trapézio maior: \( BC = 27\,\text{cm} \)
- Altura do trapézio menor: \( NP = 18\,\text{cm} \)
Vamos calcular a razão de semelhança:
\[ k = \frac{18}{27} = \frac{2}{3} \]
Com isso, podemos calcular a base menor do trapézio menor:
\[ MN = AB \cdot k = 25 \cdot \frac{2}{3} = \frac{50}{3} \approx 16{,}67\,\text{cm} \]
- Qual é a base menor do trapézio menor \( MN \), sabendo que a razão de semelhança é \( \frac{2}{3} \)?
- Sabendo que \( BC = 27\,\text{cm} \) e \( NP = 18\,\text{cm} \), qual é a razão de semelhança entre os trapézios?
✅ Resposta: As figuras são semelhantes, pois possuem ângulos congruentes e lados proporcionais. A razão de semelhança é \( \dfrac{2}{3} \) e a base menor do trapézio menor é aproximadamente 16,67 cm.
📚 Continue estudando com nossos materiais gratuitos:
🔷 Leia também: Polígonos Semelhantes: Como Identificar e Aplicar na Prática
Aprenda de forma clara como reconhecer quando dois polígonos são semelhantes, com exemplos, aplicações no cotidiano, explicações visuais e dicas para resolver questões com confiança. Ideal para estudantes e professores!
👉 Acessar o artigo completo












