Feixe de Retas Paralelas
Duas ou mais retas paralelas entre si, pertencentes a um mesmo plano, formam um feixe de retas paralelas. Uma reta que intersecta esse feixe de paralelas é chamada de reta transversal.
Na figura abaixo, as retas \( a, b, c \) e \( d \) formam um feixe de retas paralelas, enquanto as retas \( r \) e \( t \) são transversais:
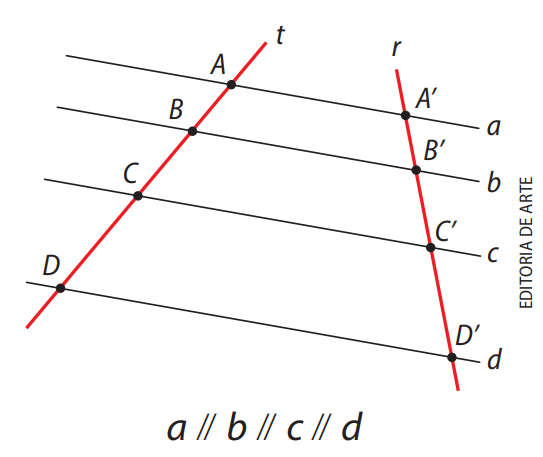
Figura: Retas paralelas e transversais
Podemos definir os pontos correspondentes e os segmentos correspondentes com base na interseção dessas retas:
Pontos Correspondentes:
- \( A \) e \( A’ \)
- \( B \) e \( B’ \)
- \( C \) e \( C’ \)
- \( D \) e \( D’ \)
Segmentos Correspondentes:
- \( \overline{AB} \) e \( \overline{A’B’} \)
- \( \overline{BC} \) e \( \overline{B’C’} \)
- \( \overline{CD} \) e \( \overline{C’D’} \)
- \( \overline{AC} \) e \( \overline{A’C’} \)
- \( \overline{AD} \) e \( \overline{A’D’} \)
- \( \overline{BD} \) e \( \overline{B’D’} \)
A relação de paralelismo entre essas retas é representada por:
\( a \parallel b \parallel c \parallel d \)
Aplicações do Feixe de Retas
O estudo de feixes de retas paralelas é fundamental em diversas áreas da geometria, especialmente ao tratar de proporcionalidade de segmentos, semelhança de triângulos e teoremas como o de Tales.
🧠 Reforço Visual e Prático
Para fixar esse conteúdo com ainda mais clareza e praticidade, confira nossos recursos gratuitos:

























