Enunciado:
Clara precisa resolver o seguinte problema em sua aula de Matemática:
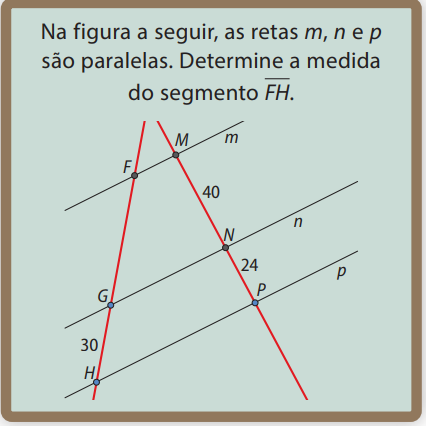
Na figura a seguir, as retas \( m, n \) e \( p \) são paralelas. Determine a medida do segmento \( \overline{FH} \).
Para resolver o problema, Clara utilizou a proporção:
\( \frac{FH – 30}{30} = \frac{40}{24} \)
Reúna-se a um colega e respondam às questões:
- A proporção apresentada por Clara está correta? Justifiquem.
- Essa proporção resolve o problema? Justifiquem.
- Existe outra proporção que resolve o problema? Se sim, escrevam-na.
👇 Ver solução passo a passo
a) A proporção de Clara está correta?
Sim. Clara está comparando segmentos correspondentes das transversais que cruzam as retas paralelas:
- \( FH – 30 \) é o segmento \( FG \);
- \( GH = 30 \);
- \( MP = 40 \);
- \( PG = 24 \).
A proporção está montada entre segmentos correspondentes, portanto é válida.
b) Essa proporção resolve o problema?
Sim. Podemos resolver a equação a partir dela:
\( \frac{FH – 30}{30} = \frac{40}{24} \Rightarrow FH – 30 = \frac{40 \cdot 30}{24} = 50 \Rightarrow FH = 80 \)
c) Outra proporção possível:
\( \frac{FH}{30} = \frac{64}{24} \)
Aqui, Clara soma os segmentos da transversal da esquerda (\( FG + GH = FH \)) e compara com a soma dos segmentos da transversal da direita (\( MP + PG = 64 \)). A proporção continua válida.
Resposta final: \( FH = \boxed{80} \)
🔗 Material complementar gratuito
📌 Quer praticar mais?
Confira uma seleção incrível com 8 exercícios resolvidos sobre Teorema de Tales e Proporcionalidade, todos com figuras, explicações detalhadas e solução passo a passo com botão de abre/fecha:













