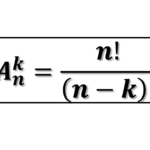A análise combinatória é uma área fascinante da matemática que usamos mais do que imaginamos, mesmo sem perceber. Sempre que organizamos, escolhemos ou agrupamos elementos, estamos aplicando princípios desse ramo da matemática. Seja para planejar uma viagem, montar um look, ou até para ganhar na loteria (quem nunca?), a análise combinatória está presente.
Neste artigo, vamos explorar de forma humanizada o conceito de análise combinatória e entender como ela facilita situações cotidianas. Com exemplos simples e práticos, você verá como esse tema pode ser acessível e útil no seu dia a dia.
📚 Quer aprofundar seus conhecimentos em Análise Combinatória e Probabilidade? Confira nossa recomendação dos melhores livros sobre o tema com exercícios resolvidos e dicas práticas. 👉Os melhores livros de Analise Combinatória e Probabilidade
O que é Análise Combinatória?
De forma simples, a análise combinatória estuda as diferentes maneiras de combinar, organizar ou escolher elementos de um conjunto. Ela responde perguntas como:
- Quantas senhas diferentes podem ser criadas com um número limitado de dígitos?
- De quantas formas é possível organizar livros em uma prateleira?
- Quantas combinações de pratos podem ser feitas em um cardápio com entradas, pratos principais e sobremesas?
Essas perguntas podem parecer simples, mas quando os números aumentam, a contagem manual se torna inviável. É aí que entram as fórmulas e conceitos da análise combinatória.
Por Que a Análise Combinatória É Importante no Dia a Dia?
A análise combinatória não está limitada ao ambiente acadêmico ou a provas de concursos. Ela aparece frequentemente em situações rotineiras. Aqui estão alguns exemplos práticos:
Montar Looks de Roupas Imagine que você tem 3 camisetas e 2 calças no guarda-roupa. Quantos looks diferentes você pode montar? Basta multiplicar as opções:
3 (camisetas) × 2 (calças) = 6 looks diferentes
Um conceito simples, mas que já demonstra o princípio básico da contagem.
Planejamento de Viagens Suponha que você tenha 4 cidades para visitar e deseja saber em quantas ordens diferentes pode organizá-las no roteiro. Aqui entra o conceito de permutação, que é uma forma de organizar elementos. Para 4 cidades, existem 24 maneiras diferentes de planejar sua viagem.
Senhas e Segurança Pense em um cadeado que exige uma senha de 4 números, onde cada dígito pode variar de 0 a 9. Quantas senhas diferentes podem ser criadas? Usando o princípio fundamental da contagem:
10×10×10×10 = 10.000 senhas possíveis
Essa aplicação é crucial em segurança digital e criptografia.
Jogos e Apostas A análise combinatória é usada para calcular as chances de ganhar em loterias. Por exemplo, em uma loteria que exige escolher 6 números entre 60, há mais de 50 milhões de combinações possíveis. Saber disso pode até te ajudar a ajustar expectativas!
Princípios Básicos da Análise Combinatória
1. Princípio Fundamental da Contagem
O princípio fundamental da contagem é a base de tudo na análise combinatória. Ele afirma que, se uma tarefa pode ser feita de n maneiras e outra de mm maneiras, o total de combinações possíveis é o produto n×m
Exemplo Prático:
Se um restaurante oferece 3 tipos de entrada, 4 pratos principais e 2 sobremesas, o número de combinações possíveis de refeições completas é:
3×4×2 = 24 refeições possíveis
2. Permutação
A permutação é a organização de elementos em ordem específica. Se você tem nn elementos, o número de permutações possíveis é dado por:
n!=n×(n−1)×(n−2)⋯×1
Exemplo Prático:
Quantas maneiras diferentes existem para organizar 5 livros em uma prateleira?
5!=5×4×3×2×1 = 120 maneiras diferentes
3. Combinação
A combinação se refere a selecionar elementos sem se preocupar com a ordem. É especialmente útil em situações como formar grupos ou times. A fórmula para combinação é:
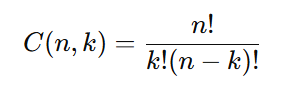
Exemplo Prático:
Em uma turma de 10 alunos, quantos grupos de 3 podem ser formados para um trabalho
C(10,3)=10!3!(10−3)!=10×9×83×2×1=120 grupos possíveis.
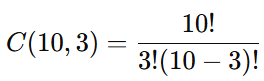
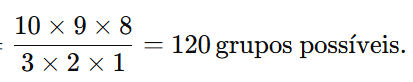
Como a Análise Combinatória Ajuda em Concursos?
A análise combinatória é um dos temas mais cobrados em provas de concursos e vestibulares. Questões como “De quantas maneiras diferentes um comitê pode ser formado?” ou “Quantos anagramas podem ser feitos com uma palavra?” aparecem com frequência.
Saber aplicar as fórmulas de forma prática é essencial para resolver essas questões rapidamente. Além disso, dominar o tema pode ser um diferencial importante, já que muitos candidatos têm dificuldade com ele.
Conclusão
A análise combinatória é muito mais do que um tema teórico da matemática. Ela está presente no nosso cotidiano de maneiras surpreendentes, ajudando a resolver problemas de organização, planejamento e escolha. Com os exemplos simples que vimos aqui, fica claro como ela pode ser útil tanto para situações práticas quanto para alcançar sucesso em provas e concursos.
Agora que você já entende os conceitos básicos e viu como aplicá-los no dia a dia, que tal explorar mais a fundo o tema? Descubra como permutações, arranjos e combinações podem transformar sua forma de pensar sobre contagem e organização. E lembre-se: quanto mais você praticar, mais fácil será dominar esse assunto!
Exercícios Práticos de Análise Combinatória com Soluções
Aqui estão alguns exercícios práticos sobre análise combinatória, com soluções detalhadas para ajudar na compreensão.
Exercício 1: Planejamento de Looks
Você tem 4 camisetas e 3 calças no guarda-roupa. Quantos looks diferentes você pode montar?
Ver Solução
Solução:
Para cada camiseta, você pode combinar com qualquer uma das 3 calças.
O número total de combinações é dado pelo princípio fundamental da contagem:
4 (camisetas) × 3 (calças = 12 looks diferentes
Resposta: 12 looks.
Exercício 2: Organização de Livros
Você tem 5 livros diferentes para organizar em uma prateleira. De quantas formas diferentes é possível organizá-los?
Ver Solução
Solução:
Como a ordem importa, usamos a fórmula de permutação:
P(5) = 5!=5×4×3×2×1 =120
Resposta: 120 formas diferentes.
Exercício 3: Formando Grupos
Em uma turma de 8 alunos, quantos grupos de 3 podem ser formados?
Ver Solução
Solução:
Como a ordem não importa, usamos a fórmula de combinação:
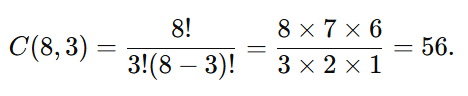
Resposta: 56 grupos.
Exercício 4: Criando Senhas
Quantas senhas de 4 dígitos podem ser formadas, considerando que cada dígito pode variar de 0 a 9?
Ver Solução
Solução:
Cada dígito possui 10 opções (de 0 a 9).
Pelo princípio fundamental da contagem, o número total de senhas é:
10×10×10×10 = 10.000
Resposta: 10.000 senhas possíveis.
Exercício 5: Sorteio de Pessoas
Uma empresa realizará um sorteio para selecionar 2 funcionários entre
8 participantes. Quantas duplas diferentes podem ser formadas?
Ver Solução
Solução:
Como a ordem dos escolhidos não importa, usamos a fórmula de combinação:
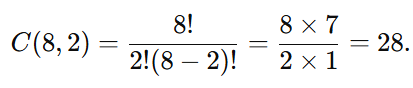
Resposta: 28 duplas diferentes.
Exercício 6: Anagramas de uma Palavra
Quantos anagramas podem ser formados com as letras da palavra “AMOR”?
Ver Solução
Solução:
A palavra “AMOR” possui 4 letras diferentes.
Para calcular o número de anagramas, usamos a fórmula de permutação:
P(4) = 4!=4×3×2×1 = 24
Resposta: 24 anagramas possíveis.
Exercício 7: Cardápio de Refeições
Um restaurante oferece 3 tipos de entrada, 5 pratos principais e 2 sobremesas. Quantas combinações completas de refeições (entrada + prato principal + sobremesa) podem ser feitas?
Ver Solução
Solução:
Aplicamos o princípio fundamental da contagem:
3 (entradas) × 5 (pratos principais) ×2 (sobremesas) = 30 refeições possíveis
Resposta: 30 combinações de refeições.
Exercício 8: Seleção de Representantes
Uma escola precisa selecionar 1 presidente, 1 vice-presidente e 1 secretário entre 6 candidatos. De quantas maneiras diferentes isso pode ser feito?
Ver Solução
Solução:
Aqui a ordem importa, então usamos a fórmula de arranjo:
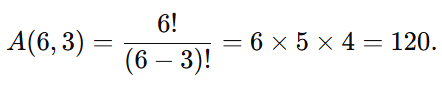
Resposta: 120 maneiras diferentes.
Esses exercícios cobrem os principais conceitos de análise combinatória: princípio fundamental da contagem, permutação, combinação e arranjo. Com a prática, fica cada vez mais fácil resolver problemas desse tipo!
