Domine Análise Combinatória com esta lista completa de exercícios resolvidos passo a passo. Ideal para quem está se preparando para concursos, vestibulares e o ENEM. Aprenda a resolver problemas de permutação, arranjo, combinação e muito mais com explicações claras e objetivas. Confira agora e aprimore seus estudos de matemática!
Questão 1:
Para completar o álbum de figurinhas da Copa do Mundo, são necessárias 670 figurinhas diferentes. Sabendo-se que cada pacotinho contém 5 figurinhas, todas distintas, o total de pacotinhos diferentes que podem ser formados com as figurinhas do álbum pode ser calculado por meio do produto:
a) 67 × 223 × 167 × 667 × 666
b) 67 × 669 × 668 × 667 × 666
c) 67 × 223 × 167 × 667 × 222
d) 670 × 669 × 668 × 667 × 666
e) 6705
Ver Solução
Resposta: Letra A
Solução:
Como temos 670 figurinhas diferentes e queremos formar pacotinhos com 5 figurinhas distintas, usamos a combinação simples:

O produto que representa esse cálculo corresponde à alternativa A:
67 × 223 × 167 × 667 × 666
Questão 2:
Em uma escola de São Paulo, o uso do uniforme é obrigatório. Para que esse uso seja mais divertido, os alunos podem escolher diferentes cores de camisetas: branca, amarela ou azul. A calça comprida e a bermuda são cinza.

A) Calcule a quantidade de combinações diferentes que podem ser feitas com essas peças do uniforme.
B) Considerando que os alunos podem estar com ou sem casaco, calcule o número total de combinações possíveis.
Ver Solução
Resposta: a) 6 combinações – b) 12 combinações
Solução:
- a) Camiseta (3 cores) × parte inferior (calça ou bermuda = 2) = 3 × 2 = 6
- b) Incluindo o casaco (com ou sem = 2): 3 × 2 × 2 = 12
Questão 3:
Numa sorveteria, há 3 tipos de sorvete: picolé, casquinha e copinho.

Juliana vai comprar sorvete para seus 3 netos, e os sorvetes podem ser ou não do mesmo tipo. Determine o total de possibilidades para essa compra.
Ver Solução
Resposta: 27
Solução:
Para cada um dos 3 netos, há 3 opções de sorvete: 3×3×3=27 possibilidades
Questão 4:
Camila vai escolher uma senha para sua primeira conta bancária. A senha será de seis campos, sendo que:
- Os dois primeiros campos têm que ser símbolos, iguais ou distintos, do conjunto {#, &};
- Os dois campos seguintes devem ser elementos do conjunto {a, b, A, B}, iguais ou distintos (note que “aA” constitui senha diferente de “AA”);
- Os dois últimos campos devem ser elementos do conjunto {0, 2, 4}, iguais ou distintos.
Sendo assim, o maior número de senhas diferentes que Camila poderá escolher é igual a:
a) 144
b) 288
c) 576
d) 524
e) 432
Ver Solução
Resposta: Letra C
Solução:
Número total de senhas possíveis: (2 símbolos)2×(4 letras)2×(3 dígitos)2=2×2×4×4×3×3=576
Questão 5:
A soma dos coeficientes binomiais com numerador 2022 é:
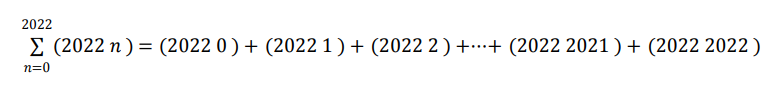
Esse valor equivale a:
a) 4¹⁰¹¹
b) 2⁴⁰⁴⁴
c) 2¹⁰¹¹
d) (2)²⁰²³
e) (2)¹⁰¹¹
Ver Solução
Resposta: Letra A
Solução:
A soma dos coeficientes binomiais de linha 2022 é 22022 = (21011)2 = 41011 = 41011
Questão 6:
A senha de acesso à conta-corrente de um banco deve ser composta por quatro algarismos distintos, escolhidos entre os algarismos 1, 3, 4, 5, 7, 8 e 9. Nesse caso, a quantidade de senhas que têm como último dígito um algarismo par é:
a) 120
b) 240
c) 360
d) 600
e) 16.400
Ver Solução
Resposta: Letra B
Solução:
Último dígito deve ser par (4 ou 8) → 2 opções
Sobram 6 algarismos para os 3 primeiros dígitos, pois devem ser distintos: 2×A(6,3) = 2×(6×5×4) = 240
Questão 7:
Utilizando os algarismos de 1 a 9, foram escritos números ímpares, de três algarismos distintos, de forma que nenhum deles termine com 1. A quantidade desses números é:
a) 224
b) 264
c) 280
d) 320
Ver Solução
Resposta: Letra A
Solução:
Números ímpares com 3 dígitos distintos sem terminar com 1. Finais possíveis: 3, 5, 7, 9 (4 opções)
Para cada: 8 × 7 possibilidades restantes: 4×8×7=224
Questão 8:
Quantos são os números inteiros positivos com três dígitos nos quais aparecem apenas os algarismos 1 e 3, repetidos ou não, que são divisíveis por 5?
a) 6
b) 15
c) 9
d) 12
Ver Solução
Resposta: Letra C
Solução:
Apenas algarismos 1 e 3, terminando em 5 (para ser divisível por 5).
Unidades: 1 opção (5)
Dezenas e centenas: 3 × 3 = 9 possibilidades 3×3=9
Questão 9:
O número de anagramas da palavra COMUM nos quais as duas letras M não aparecem juntas é:
a) 18
b) 24
c) 36
d) 48
e) 60
Ver Solução
Resposta: Letra C
Solução:
Total de anagramas de “COMUM” com duas letras M:
Total geral: 5!/2! = 60
Com os dois M juntos (como uma única letra): 4!=24
Logo, separados: 60 − 24 = 36
Questão 10:
No rancho de uma unidade militar há a opção de três pratos de proteína (frango, bife e ovo), três pratos de acompanhamento (farofa, arroz e macarrão) e dois pratos de sobremesa (doce de leite e gelatina). Os militares devem pegar apenas um item de cada prato.
Desta forma, podem-se montar quantos tipos de refeições distintas?
a) 14
b) 12
c) 18
d) 16
e) 10
Ver Solução
Resposta: Letra C
Solução:
Opções:
- Proteína: 3
- Acompanhamento: 3
- Sobremesa: 2
Total:
3 × 3 × 2 = 18
Análise Combinatória: Questões Resolvidas com Explicações Passo a Passo
Análise Combinatória: 10 Questões Resolvidas com Explicações Detalhadas