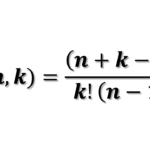Dê continuidade à sua preparação com mais uma sequência de 10 questões resolvidas de Análise Combinatória, agora numeradas de 1 a 10, acompanhadas de explicações passo a passo e comentários sobre os principais conceitos envolvidos.
Você vai revisar conteúdos como permutação, combinação, princípio multiplicativo, aplicações do Triângulo de Pascal, princípio das gavetas (pombos), análise de senhas, entre outros.
Ideal para quem busca consolidar o aprendizado e se preparar para concursos, ENEM e vestibulares com segurança.
Aproveite esta coletânea para testar seu conhecimento e reforçar sua prática com resoluções claras, diretas e fundamentadas.
Aqui está a lista completa das questões de 31 a 40, com alternativas (quando houver), respostas e explicações detalhadas, prontas para o seu blog:
Questão 1: Um caixeiro viajante parte de uma cidade A com destino a uma cidade B, passando uma única vez por outras 4 cidades. De quantas formas distintas esse trajeto pode ser feito?
Alternativas:
a) 24
b) 15
c) 12
d) 1
e) 32
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Resposta: a) 24
Solução:
Temos 4 cidades intermediárias e queremos organizá-las em todas as ordens possíveis entre A e B. Isso é uma permutação:
P(4)=4!=4⋅3⋅2⋅1=24
Ou seja, há 24 rotas distintas entre A e B passando pelas 4 cidades.
[/toggle]
Questão 2: Resolva a equação: C(10,5) + C(10,6) = C(11,x)
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Resposta: x = 6
Solução:
Usamos a relação de Stifel: C(n, k) + C(n, k+1) = C(n+1, k+1)
Aplicando: C(10, 5) + C(10, 6) = C(11, 6)
Logo, x = 6
[/toggle]
Questão 3: Um motor de 3800 cilindradas possui cilindros com capacidades diferentes: 200, 250, 300, 400, 800 e 1850 cm³. Considerando a tecnologia de desativação de cilindros, quantas combinações possíveis de motorização (diferentes somas) podem ser formadas?
Alternativas:
a) 30
b) 63
c) 64
d) 36
e) 72
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Resposta: c) 64
Solução:
Esse é um problema típico de número de subconjuntos não vazios.
Com 6 valores distintos → número de subconjuntos = 26 = 64
[/toggle]
Questão 4: Utilize o Triângulo de Pascal para calcular: C(1,0) + C(2,1) + C(3,0)
Alternativas:
a) 0
b) 1
c) 2
d) 3
e) 4
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Resposta: e) 4
Solução:
Basta somar os valores binomiais: C(1,0) = 1, C(2,1) = 2, C(3,0) = 1 ⇒ 1 + 2 + 1 =4
[/toggle]
Questão 5: Quantos anagramas podem ser formados com a palavra FOXTROT?
Alternativas:
a) 10.080
b) 1.260
c) 2.520
d) 1.680
e) 5.040
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Resposta: a) 10.080
Solução:
A palavra FOXTROT tem 7 letras, com o T repetido duas vezes:
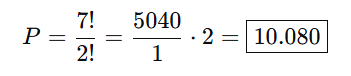
[/toggle]
Questão 6: Num almoço de casamento, há uma mesa redonda com os noivos, 5 familiares do noivo e 6 da noiva. Quantas formas diferentes os 13 convidados podem se sentar, com os noivos sempre juntos?
Alternativas:
a) 11!
b) 2 · 11!
c) 12!
d) 13!
e) 2 · 13!
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Resposta: b) 2 · 11!
Solução:
- Como os noivos devem ficar juntos, tratamos como um “bloco”, restando 12 blocos.
- Em mesa redonda, a permutação de nn pessoas com 1 referência fixa é:
(n – 1)!
- Mas os noivos podem inverter de posição → multiplicamos por 2:
(12 − 1)!⋅2 = 11! ⋅ 2 = 2⋅11!
[/toggle]
Questão 7: A Copa do Brasil teve, até a edição de 2018, 15 times diferentes como campeões da competição, conforme apresentado na imagem.
Suponha que, como homenagem aos times campeões, a Confederação Brasileira de Futebol (CBF) pretenda colocar um painel na sua sede. Esse painel teria 6 linhas e, em cada uma delas, 5 placas, referentes a cada edição da competição, como o nome do time vencedor, o brasão e o ano do título. O painel dever ser fabricado de modo que a primeira linha só tenha clubes gaúchos (Internacional, Grêmio e Juventude); a segunda, apenas times cariocas (Flamengo, Vasco e Fluminense); a terceira, somente times mineiros (Cruzeiro e Atlético Mineiro); a quarta, exclusivamente clubes paulistas (Corinthians, Palmeiras, Santos, Paulista FC, Santo André), e as duas últimas sem nenhuma restrição.
Qual expressão determina a quantidade de painéis diferentes que a CBF poderá montar?

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Como temos uma distribuição dos painéis com restrição, começamos pelas restrições:
Primeira Linha
Para a primeira linha só poderão entrar clubes gaúchos: Internacional, Grêmio e Juventude; Ao todo destes três clubes, temos títulos ao total, assim:
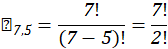
Segunda Linha
Para a segunda linha, apenas times cariocas: Flamengo, Vasco e Fluminense; Ao todo, temos títulos ao total, assim:
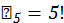
Terceira Linha
Para a terceira linha, somente times mineiros: Cruzeiro e Atlético Mineiro; Ao todo, temos títulos, assim:
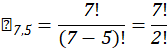
Quarta Linha
Para a quarta linha, exclusivamente clubes paulistas: Corinthians, Palmeiras, Santos, Paulista FC, Santo André; Ao todo temos, títulos, assim:
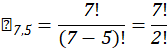
Quinta Linha
Para a quinta linha, não temos restrição de clubes, assim, entrarão quaisquer títulos:
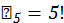
Sexta Linha
Assim como na linha anterior, por não ter restrição, serão distribuídos, quaisquer títulos:
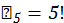
Portanto, o número de painéis distintos que poderão ser montados é igual a:
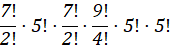
A questão foi modificada para apresentar uma alternativa correta.
[/toggle]
Questão 8: Dado um grupo com 5 alunos e 6 professores, quantas comissões de 4 pessoas podem ser formadas, com no mínimo 3 professores?
Alternativas:
a) 95
b) 100
c) 105
d) 107
e) 115
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Resposta: c) 105
Solução:
Casos possíveis:
🔹 3 professores e 1 aluno: C(6, 3)⋅C(5, 1) = 20⋅5 = 100
🔹 4 professores: C(6, 4) = 15
Total: 100 + 15 = 105
[/toggle]
Questão 9: Em uma urna há bolas de 5 cores:
- 7 brancas,
- 10 pretas,
- 13 azuis,
- 17 vermelhas,
- 23 amarelas
Qual o mínimo número de bolas que devem ser retiradas para garantir que haja 16 da mesma cor?
Alternativas:
a) 16
b) 23
c) 46
d) 61
e) 66
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
Estratégia (Princípio da Casa dos Pombos):
Vamos considerar o pior cenário, ou seja, retirar o máximo de bolas sem atingir 16 de nenhuma cor:
- 7 brancas (limite total)
- 10 pretas (limite total)
- 13 azuis (limite total)
- 15 vermelhas (ainda sobra 2)
- 15 amarelas (ainda sobra 8)
Total até aqui: 7+10+13+15+15=607 + 10 + 13 + 15 + 15 = 607+10+13+15+15=60
Se retirarmos mais 1 bola, teremos 16 de alguma cor garantidamente, pois as opções “seguras” já se esgotaram.
✅ Resposta Final: 61 bolas
Alternativa correta: d) 61
[/toggle]