Confira mais 10 questões selecionadas de Análise Combinatória , todas resolvidas com explicações detalhadas para facilitar seu aprendizado. Esta lista é ideal para quem está se preparando para concursos, vestibulares e o ENEM, abordando temas como anagramas, permutação com repetição, princípio multiplicativo, combinação, arranjos e mais.
Estude com exemplos práticos, visualize a lógica por trás das fórmulas e aprenda a resolver cada problema com clareza.
Aperfeiçoe seus conhecimentos e turbine sua preparação em matemática!
Aqui está a lista completa das questões de 21 a 30 com alternativas, respostas e explicações melhoradas, pronta para publicação no seu blog:
Questão 1: Considerando todos os anagramas distintos que se pode formar com todas as letras da palavra MATEMATICA (sem acento), qual a quantidade de anagramas em que todas as vogais aparecem juntas?
a) 6!
b) 5 · 6!
c) 6!/4
d) 10!/24
Ver Solução
Resposta: b) 5 · 6!
Solução:
As vogais (A, A, A, E, I) serão agrupadas como um único bloco. Então temos:
- Permutação dos 6 elementos restantes (5 consoantes + 1 bloco de vogais):

- Permutação das vogais dentro do bloco (com 3 letras A):
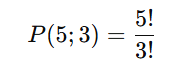
Multiplicando:
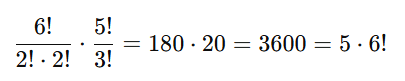
Questão 2: Se 8 alunos do CFS da EEAR “entram em forma” em uma única fila, de forma que o aluno mais alto sempre fique no início da fila, quantas formações diferentes são possíveis?
a) 5.040
b) 2.520
c) 840
d) 720
Ver Solução
Resposta: a) 5.040
Solução:
Fixando o aluno mais alto na primeira posição, sobram 7 alunos para permutar:
7! = 5.040
Questão 3: Com base em um modelo de confecção de máscaras caseiras com 5 especificações (tipo, cor, lados internos, lados externos, padrões), quantas máscaras diferentes podem ser feitas?
a) 12
b) 14
c) 36
d) 72
Ver Solução
Resposta: d) 72
Solução:
Multiplicamos o número de opções em cada categoria: 2 (tipos)⋅3 (cores)⋅2 (lados internos)⋅3 (lados externos)⋅2 (padrões) = 72
Questão 4: Simplificando a expressão
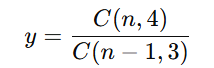
qual o valor de y?
a) n
b) n/2
c) n/3
d) n/4
Ver Solução
Resposta: d) n/4
Solução:
Utilizando as fórmulas de combinação:
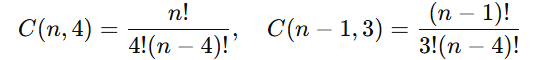
Dividindo:

Questão 5: Dado um cubo, quantos pares distintos de retas reversas (ou seja, que nunca se encontram e não são paralelas) podem ser formados usando as arestas do cubo?
a) 24
b) 30
c) 36
d) 42
e) 48
Ver Solução
Resposta: a) 24
Solução:
Cada uma das 12 arestas do cubo forma 4 pares reversos, totalizando 12⋅4 = 48
Como estamos contando em duplicidade (A com B e B com A), dividimos por 2:
48 / 2 = 24
Questão 6: Dado um dodecaedro regular, quantas retas podem ligar dois de seus vértices sem estarem na mesma face?
a) 60
b) 100
c) 130
d) 160
e) 190
Ver Solução
Resposta: b) 100
Solução:
- Total de vértices: 20
- Total de pares possíveis: C(20, 2) = 190
- Subtraímos as 30 arestas e 60 diagonais de face:
190 – 30 – 60 = 100
Questão 7: Em um diagrama de ruas de mão única com 13 segmentos, quantos caminhos diferentes existem para ir do ponto P até o ponto Q, respeitando os sentidos das vias?
a) 8
b) 10
c) 6
d) 9
e) 7
Ver Solução
Resposta: c) 6
Solução:
Verificando manualmente as possíveis rotas sem pegar “contramão”, identificamos 6 trajetos distintos.
Questão 8: Quantos números ímpares de cinco algarismos podem ser formados com: dois algarismos 1, dois algarismos 2 e um algarismo 3?
a) 6
b) 12
c) 18
d) 24
e) 26
Ver Solução
Resposta: c) 18
Solução:
Como o número deve ser ímpar, o último dígito deve ser 1 ou 3.
- Final com 1 → permutação dos 4 restantes: P(4;2) = 12
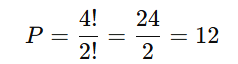
- Final com 3 → permutação dos 4 restantes: P(4;2,2) = 6
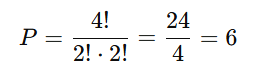
12 + 6 = 18 números
Questão 9: Dentre 24 personagens em um jogo (10 magos, 8 guerreiros e 6 curandeiros), deseja-se formar grupos com 2 magos, 1 guerreiro e 1 curandeiro. Quantos grupos distintos podem ser formados?
a) 35
b) 48
c) 360
d) 2.160
e) 4.320
Ver Solução
Resposta: d) 2.160
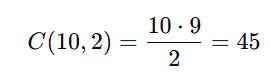

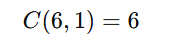
Solução: C(10,2)⋅C(8,1)⋅C(6,1)=45⋅8⋅6 = 2.160
Questão 10: Sendo C(n+1, k) = C(n+1, k+1), mostre que n é um número par.
Ver Solução
Resposta: n = 2k
Solução:
A igualdade só é válida quando:
k = k+1 ⇒ impossível ou k+(k+1) = n+1 ⇒ n = 2k
Portanto, n deve ser par.
Análise Combinatória: 10 Questões Resolvidas com Explicações Detalhadas
Análise Combinatória: Lista de Exercícios com Solução