Arranjo com Repetição: Domine Esse Conceito

O arranjo com repetição é uma das ferramentas fundamentais da análise combinatória, permitindo calcular o número de maneiras de organizar elementos de um conjunto quando a ordem importa e os elementos podem ser repetidos. Esse conceito é amplamente utilizado em problemas práticos e teóricos da matemática, como na criação de senhas, combinações de cores e distribuição de objetos.

Neste artigo, vamos explorar o que é arranjo com repetição, apresentar a fórmula, exemplos práticos e resolver exercícios para consolidar o aprendizado.

Transforme seus estudos com o eBook Matemática Resumida: + de 90 Mapas Mentais de Matemática! Simplifique conceitos complexos, organize seus estudos e revise de forma prática e eficiente. Baixe agora e conquiste seus objetivos!

O Que é Arranjo com Repetição?

O arranjo com repetição ocorre quando selecionamos kk elementos de um conjunto de nn elementos, permitindo que os mesmos itens sejam escolhidos mais de uma vez. A ordem dos elementos no arranjo é relevante, ou seja, trocar a posição dos itens gera um arranjo diferente.

Por exemplo:

• Se temos as letras A e B, e queremos formar arranjos de 2 letras, permitindo repetições, podemos ter: AA, AB, BA, BB.

Fórmula do Arranjo com Repetição

A fórmula para calcular o número de arranjos com repetição é:

AR(n, k) = n^kA

• n: número total de elementos no conjunto.
• k: número de elementos escolhidos para formar o arranjo.

Essa fórmula é direta porque, para cada uma das k posições do arranjo, temos n opções de escolha.

Exemplo Prático

Problema 1: Criação de Senhas

Quantas senhas de 3 dígitos podem ser criadas usando os números de 0 a 9, permitindo repetições?

Solução:

1. Total de números (n): 10 (de 0 a 9).
2. Número de posições (k): 3.
3. Aplique a fórmula:

AR(n, k) = n^k = 10³ = 1000

Resposta: É possível criar 1000 senhas diferentes.

📚 Quer aprofundar seus conhecimentos em Análise Combinatória e Probabilidade? Confira nossa recomendação dos melhores livros sobre o tema com exercícios resolvidos e dicas práticas. 👉Os melhores livros de Analise Combinatória e Probabilidade

Diferença Entre Arranjo Simples e Arranjo com Repetição

Tipo de Arranjo	Repetição Permitida?	Ordem Importa?	Fórmula
Arranjo Simples	Não	Sim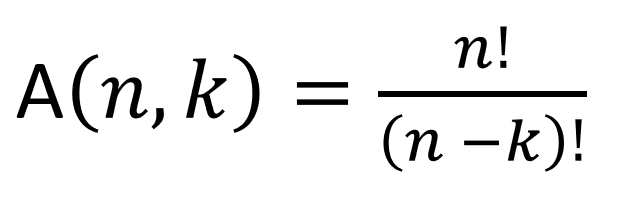
Arranjo com Repetição	Sim	Sim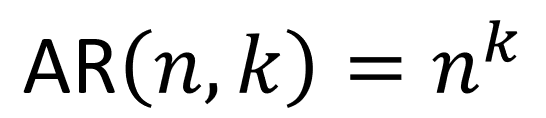

Passo a Passo para Resolver Arranjos com Repetição

1. Identifique o valor de n e k:
   Determine o número total de elementos no conjunto (n) e o número de posições do arranjo (k).
2. Verifique se há repetição e se a ordem importa:
   Se ambos forem verdadeiros, utilize a fórmula AR(n, k) = n^k
3. Aplique a fórmula:
   Substitua os valores de n e k na fórmula e calcule o resultado.

👉Entre no nosso canal do WhatsApp

📘 Todas as fórmulas de matemática em um só lugar! Baixe agora nosso eBook gratuito

Exemplos Resolvidos

Exemplo 1: Cores de Paredes

Quantas combinações diferentes podem ser feitas para pintar 2 paredes usando 4 cores diferentes, permitindo repetir cores?

Solução:

1. Total de cores (n): 4.
2. Número de paredes (k): 2.
3. Aplique a fórmula:

AR(n, k) = n^k = 4² = 16

Resposta: Existem 16 combinações possíveis.

Exemplo 2: Combinações de Letras

Quantas palavras de 4 letras podem ser formadas usando as letras A, B e C, permitindo repetições?

Solução:

1. Total de letras (n): 3.
2. Número de posições (k): 4.
3. Aplique a fórmula:

AR(n, k) = n^k = 3⁴ = 81

Resposta: Podem ser formadas 81 palavras diferentes.

Aplicações do Arranjo com Repetição

O arranjo com repetição tem várias aplicações práticas e teóricas na matemática e em outras áreas:

1. Criação de Senhas e Códigos:
   Determinar o número de combinações possíveis para senhas ou números de segurança.
2. Design e Moda:
   Combinar cores ou padrões repetidos em projetos criativos.
3. Jogos e Problemas de Lógica:
   Resolver quebra-cabeças que envolvem repetições e ordem.
4. Pesquisa e Ciência de Dados:
   Explorar combinações de parâmetros ou variáveis com repetições permitidas.
5. Planejamento e Organização:
   Planejar combinações em situações onde itens podem se repetir.

Resumo

O arranjo com repetição é uma ferramenta poderosa da análise combinatória, permitindo calcular rapidamente o número de maneiras de organizar elementos com repetição, onde a ordem importa. Sua fórmula, AR(n,k) = n^k, é simples e direta, tornando o conceito acessível e prático para resolver problemas em diversas áreas da matemática.

Com exemplos claros e exercícios resolvidos, agora você está preparado para aplicar esse conceito em problemas do dia a dia ou em contextos acadêmicos. Continue praticando e explorando outras ferramentas da análise combinatória para dominar o tema por completo!