O arranjo simples é um conceito fundamental na análise combinatória, usado para calcular o número de maneiras de selecionar e organizar uma parte dos elementos de um conjunto maior, onde a ordem importa. Se você já se perguntou quantas maneiras diferentes pode organizar um subconjunto de itens ou resolver problemas de organização com ordem relevante, este é o conceito ideal para explorar.
Neste artigo, vamos explicar o que é o arranjo simples, apresentar sua fórmula, demonstrar exemplos práticos e resolver exercícios detalhados. Além disso, conectaremos esse conceito à de arranjo e ao contexto geral da matemática.

Transforme seus estudos com o eBook Matemática Resumida: + de 90 Mapas Mentais de Matemática! Simplifique conceitos complexos, organize seus estudos e revise de forma prática e eficiente. Baixe agora e conquiste seus objetivos!
O Que é Arranjo Simples?
O arranjo simples ocorre quando selecionamos k elementos de um conjunto com n elementos no total, levando em conta a ordem em que eles aparecem. Diferente da combinação, aqui a ordem importa, mas, diferente da permutação, nem todos os elementos do conjunto original são utilizados.
Fórmula do Arranjo Simples
A fórmula do arranjo simples é:
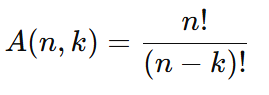
- n: número total de elementos no conjunto.
- k: número de elementos escolhidos para formar o subconjunto.
- !: fatorial, o produto de todos os números inteiros positivos até o número dado.
Exemplo Prático:
Problema 1: Organização de Medalhas
Um campeonato tem 10 participantes, mas apenas os 3 primeiros lugares recebem medalhas de ouro, prata e bronze. Quantas formas diferentes podemos organizar os vencedores?
Solução:
- Total de participantes (n): 10.
- Número de posições (k): 3.
- Aplique a fórmula:
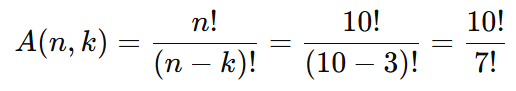
Expanda os fatoriais:
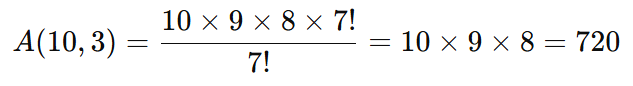
Resposta: Existem 720 maneiras diferentes de organizar os 3 primeiros lugares.
📚 Quer aprofundar seus conhecimentos em Análise Combinatória e Probabilidade? Confira nossa recomendação dos melhores livros sobre o tema com exercícios resolvidos e dicas práticas. 👉Os melhores livros de Analise Combinatória e Probabilidade
Diferença Entre Arranjo, Combinação e Permutação
| Conceito | Ordem Importa? | Usa Todos os Elementos? | Fórmula |
|---|---|---|---|
| Permutação | Sim | Sim | P(n) = n! |
| Arranjo Simples | Sim | Não | 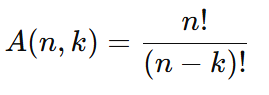 |
| Combinação | Não | Não |  |
👉Entre no nosso canal do WhatsApp
📘 Todas as fórmulas de matemática em um só lugar! Baixe agora nosso eBook gratuito
Passo a Passo para Resolver Problemas com Arranjo Simples
Identifique o valor de n e k:
Determine o número total de elementos (n) e quantos elementos serão selecionados (k).
Verifique se a ordem importa:
Se a ordem dos elementos influenciar no resultado, utilize a fórmula do arranjo simples.
Aplique a fórmula:
Substitua n e k na fórmula
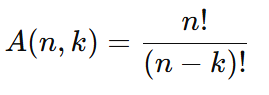
Calcule os fatoriais e simplifique.
Exemplos Resolvidos
Exemplo 1: Senhas com Dígitos
Quantas senhas de 4 dígitos podem ser formadas usando os números de 0 a 9, sem repetição?
Solução:
- Total de números (n): 10.
- Número de dígitos na senha (k): 4.
- Aplique a fórmula:
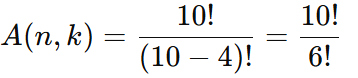
Expanda os fatoriais:
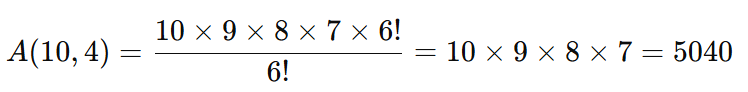
Resposta: Existem 5040 senhas possíveis.
Exemplo 2: Organização de Livros
De uma prateleira com 7 livros, queremos organizar apenas 5. De quantas maneiras diferentes isso pode ser feito?
Solução:
- Total de livros (n): 7.
- Número de livros a organizar (k): 5.
- Aplique a fórmula:
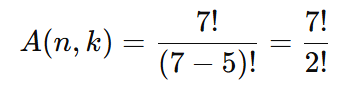
Expanda os fatoriais:
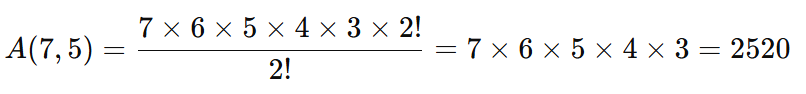
Resposta: Existem 2520 maneiras diferentes de organizar os livros.
Aplicações do Arranjo Simples
O arranjo simples é amplamente utilizado em diversas áreas práticas e acadêmicas da matemática e da análise combinatória:
- Organização de Eventos:
Planejar a ordem de apresentações ou distribuição de tarefas. - Design de Jogos:
Criar combinações únicas para jogadores ou cenários. - Criação de Senhas Seguras:
Determinar o número de possibilidades para senhas onde a ordem dos caracteres é importante. - Competição e Esportes:
Definir classificações ou rankings em competições. - Problemas de Lógica:
Resolver desafios onde a organização de elementos é essencial.
Resumo
O arranjo simples é uma ferramenta essencial na resolução de problemas de organização onde a ordem importa. Ele se destaca na análise combinatória dentro do tema arranjo por sua aplicação em situações práticas, como planejamento de eventos, criação de senhas ou organização de competições.
Com a fórmula A(n,k)=n!/(n−k)!, é possível calcular rapidamente o número de arranjos possíveis, tornando o conceito acessível e útil em diversos contextos da matemática. Agora que você domina o arranjo simples, que tal praticar mais exercícios para consolidar o aprendizado? A prática é a chave para a maestria!













