Funções, Limites, Derivadas e Integrais
O Cálculo 1 é um dos pilares da matemática no ensino superior e é essencial para estudantes de engenharia, física, ciências da computação, estatística e áreas relacionadas. Esta disciplina não trata apenas de “resolver contas”, mas de entender **como as funções variam**, como analisamos **mudanças rápidas** e **áreas sob curvas**, e como essas ideias se conectam com fenômenos do mundo real, como crescimento populacional, movimento de corpos e oscilações periódicas.
O objetivo principal do curso é desenvolver um olhar crítico e matemático sobre funções, compreendendo como elas se comportam em diferentes contextos. Para isso, utilizaremos conceitos fundamentais como limites, derivadas e integrais, que veremos em detalhes neste artigo.
1. O que é Cálculo 1?
O Cálculo 1 estuda principalmente funções reais de uma variável, ou seja, funções do tipo:
Isso significa que, para cada valor real \( x \) no domínio \( D \), a função associa um único valor real \( y \). Essas funções são estudadas a partir de ferramentas analíticas e gráficas, para que possamos prever e interpretar seu comportamento em situações práticas.
2. O que é uma Função?
Uma função é uma “máquina” matemática que transforma um número \( x \) em um resultado \( y = f(x) \). Por exemplo, se \( f(x) = 2x + 1 \), ao inserir \( x = 3 \), temos \( f(3) = 2(3) + 1 = 7 \).
**Exemplos comuns de funções:**
- Função Linear: \( \mathbf{y = 2x + 1} \) – representa uma reta.
- Função Quadrática: \( \mathbf{y = x^{2} – 4} \) – forma uma parábola.
O estudo dessas funções é essencial para compreender fenômenos físicos e econômicos, como o crescimento de preços, movimentos de objetos ou variação de temperatura.
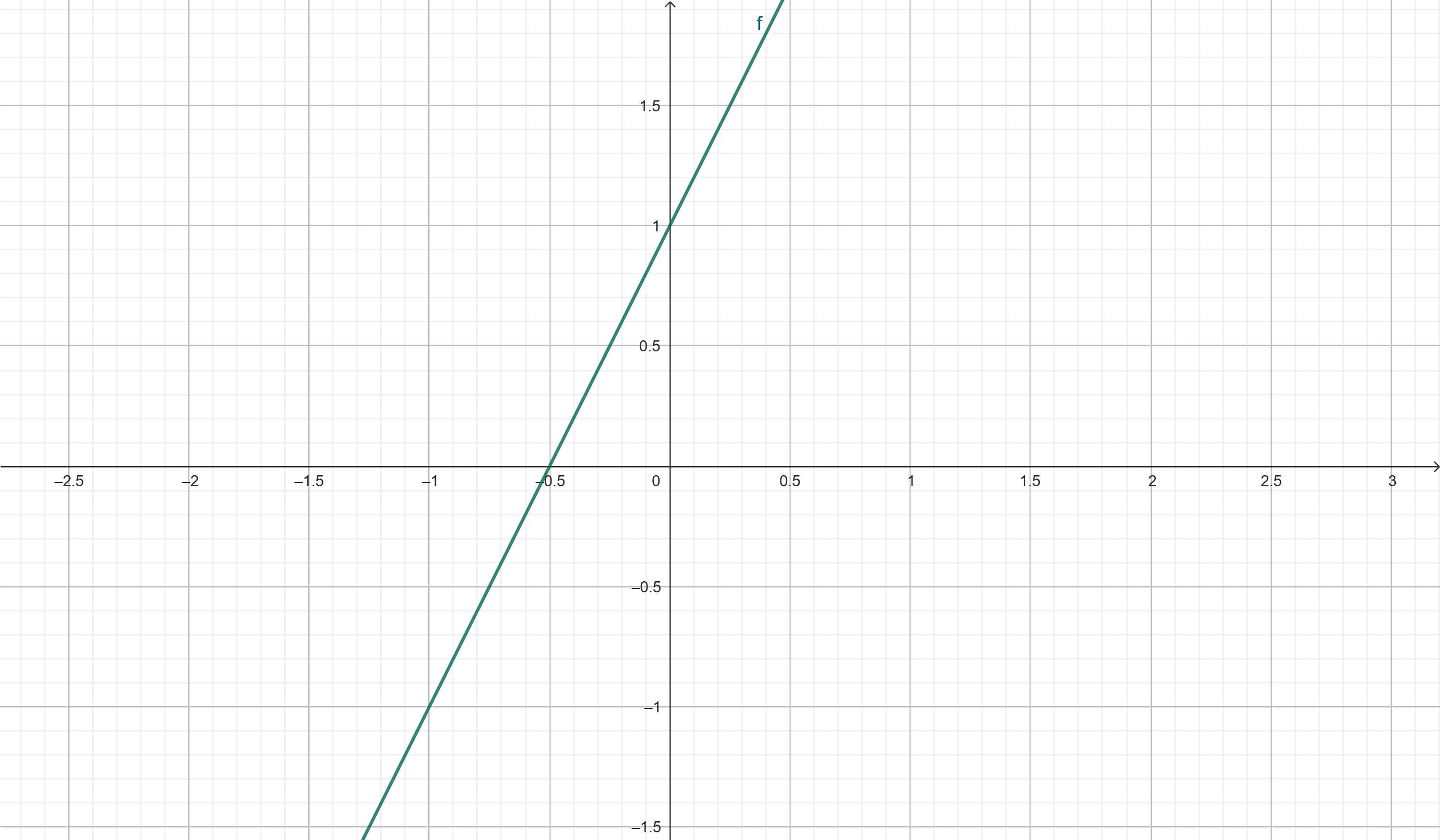
Gráfico de uma Função Linear
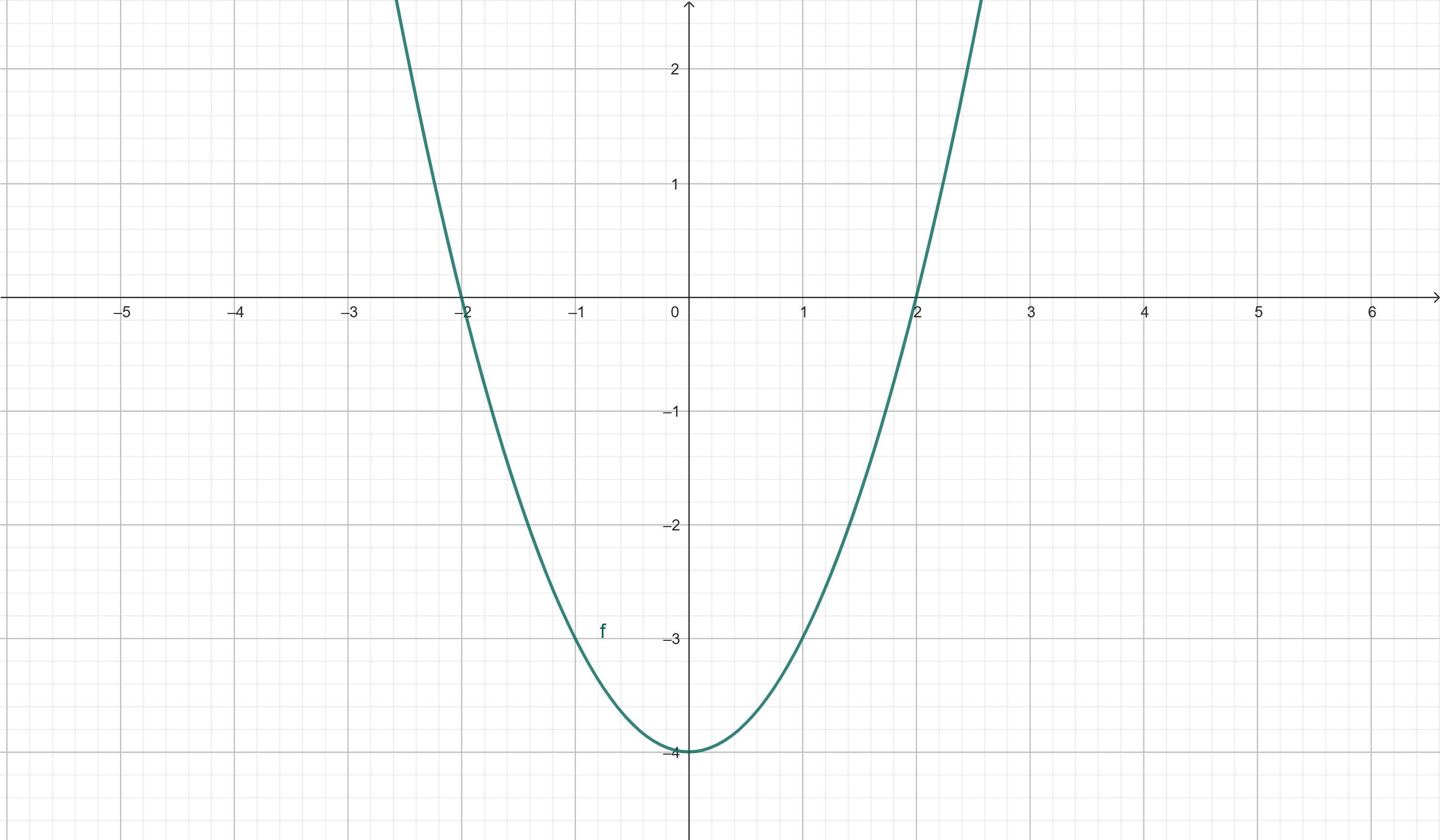
Gráfico de uma Função Quadrática
3. Limites: O Conceito de Aproximação
O conceito de limite é a base do cálculo. Ele nos permite entender o comportamento de uma função quando \( x \) se aproxima de um determinado valor. Por exemplo, se analisarmos a velocidade de um carro em um intervalo de tempo, podemos calcular a **velocidade média**:
Quando fazemos \( \Delta t \to 0 \), obtemos a **velocidade instantânea**, ou seja, a velocidade em um exato momento. Esse raciocínio é o que dá origem ao cálculo das **derivadas**.
4. Derivadas: Taxa de Variação
A derivada de uma função indica sua **taxa de variação instantânea**, ou seja, o quanto \( y = f(x) \) muda em relação a uma pequena variação de \( x \).
Graficamente, a derivada é a inclinação da reta **tangente** ao gráfico da função. Por exemplo, se a derivada em um ponto é zero, isso indica que o gráfico está “horizontal”, possivelmente em um **máximo** ou **mínimo**.
5. Integrais: A Área sob a Curva
A **integral** é usada para calcular áreas, volumes e somatórios infinitos. Em termos simples, se quisermos saber a área sob uma curva entre \( x = a \) e \( x = b \), usamos:
Esse conceito tem aplicações em cálculo de trabalho, energia, consumo acumulado e diversas áreas da ciência.
6. Exemplos de Funções
Dois gráficos clássicos estudados no Cálculo 1 são:
- Função Exponencial: \( y = e^x \), representando crescimento rápido.
- Função Seno: \( y = \sin x \), representando fenômenos periódicos, como ondas.
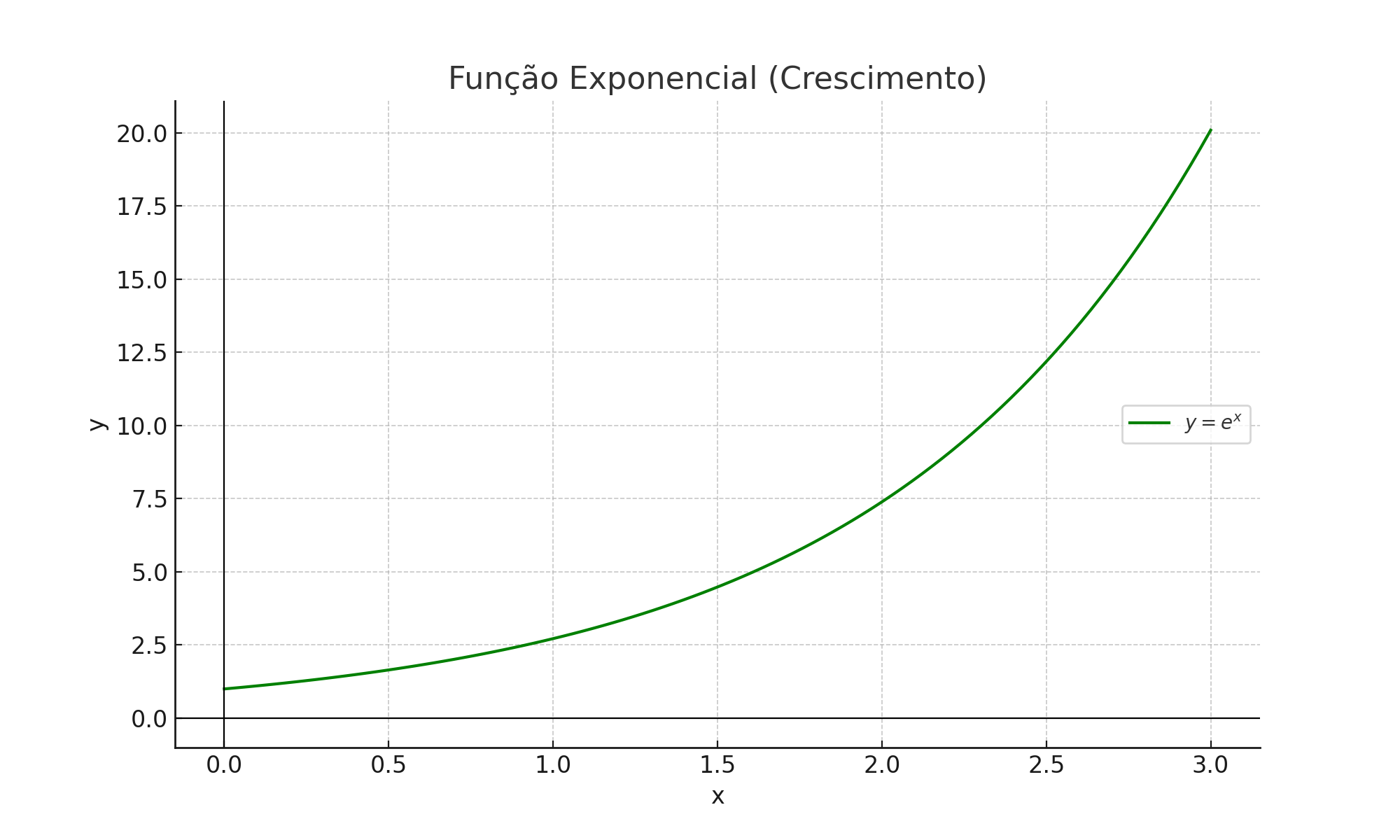
Função Exponencial (Crescimento)
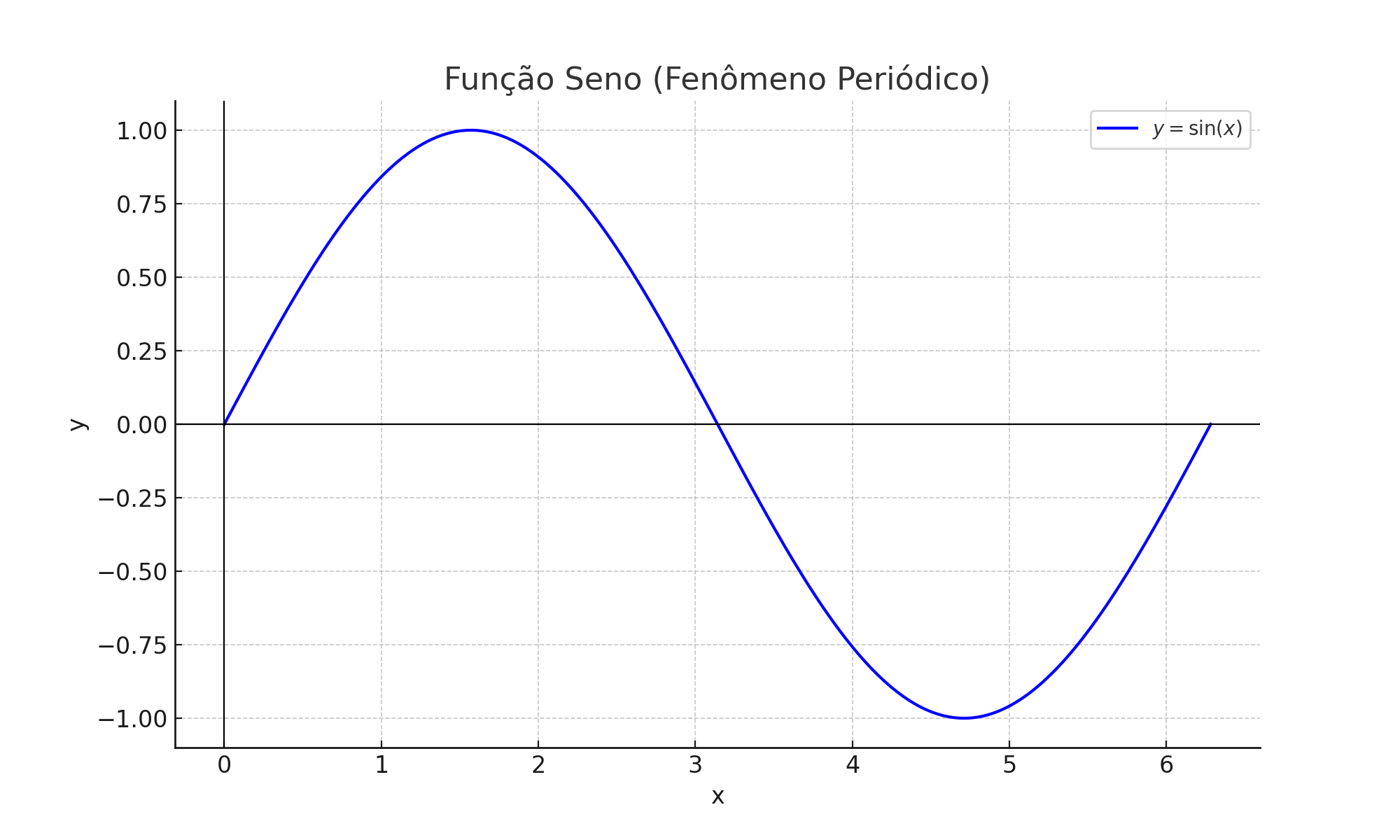
Função Seno (Fenômeno Periódico)
7. Conclusão
O estudo do Cálculo 1 abre portas para compreender o comportamento de sistemas complexos. **Limites** nos ajudam a entender aproximações, **derivadas** indicam variações instantâneas e **integrais** permitem calcular áreas e acumulados. Esses conceitos são fundamentais para aplicar a matemática em problemas reais e para seguir nos próximos níveis do cálculo.
📚 Melhores Livros de Cálculo 1
🚀 Curso Completo de Cálculo 1
Domine os fundamentos do Cálculo Diferencial e Integral com aulas passo a passo, desde funções até integrais avançadas. Ideal para universitários, concurseiros e entusiastas da matemática.
Disponível no blog Matemática Hoje