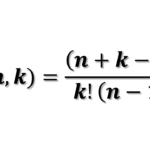A combinação simples é um conceito fundamental da análise combinatória, utilizado para calcular o número de maneiras de selecionar elementos de um conjunto sem levar em consideração a ordem. Esse princípio é amplamente utilizado em problemas práticos e teóricos da matemática, como na formação de grupos, seleção de equipes ou análise de possibilidades em pesquisas.
Neste artigo, você aprenderá o que é a combinação simples, a fórmula utilizada, exemplos práticos e exercícios resolvidos. Vamos explorar como esse conceito pode ser aplicado de forma simples e prática.

Transforme seus estudos com o eBook Matemática Resumida: + de 90 Mapas Mentais de Matemática! Simplifique conceitos complexos, organize seus estudos e revise de forma prática e eficiente. Baixe agora e conquiste seus objetivos!
O Que é Combinação Simples?
A combinação simples ocorre quando escolhemos k elementos de um conjunto com n elementos no total, sem considerar a ordem dos itens selecionados. Isso significa que trocar a posição dos elementos não cria uma nova combinação.
Por exemplo:
- Se temos as letras A, B e C, e queremos formar grupos de 2 letras, as combinações possíveis são: AB, AC e BC. Note que BA é o mesmo grupo que AB.
Fórmula da Combinação Simples
A fórmula para calcular o número de combinações simples é:
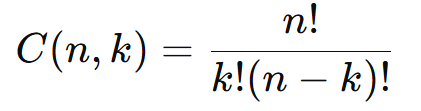
- n: número total de elementos no conjunto.
- k: número de elementos escolhidos para formar a combinação.
- !: fatorial, que é o produto de todos os números inteiros positivos de nn até 1.
Exemplo Prático
Problema 1: Formação de Grupos
De um grupo de 5 pessoas, queremos formar equipes de 2. Quantas combinações diferentes podem ser feitas?
Solução:
- Total de pessoas (n): 5.
- Número de pessoas por equipe (k): 2.
- Aplique a fórmula:
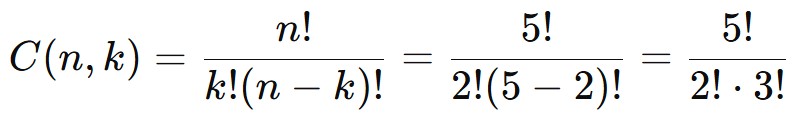
Expanda os fatoriais:
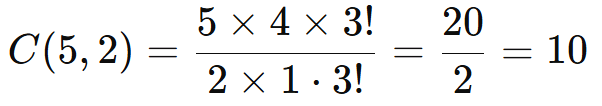
Resposta: É possível formar 10 equipes diferentes.
📚 Quer aprofundar seus conhecimentos em Análise Combinatória e Probabilidade? Confira nossa recomendação dos melhores livros sobre o tema com exercícios resolvidos e dicas práticas. 👉Os melhores livros de Analise Combinatória e Probabilidade
Diferença Entre Combinação e Arranjo
A principal diferença entre combinação e arranjo está na importância da ordem dos elementos:
| Conceito | Ordem Importa? | Fórmula |
|---|---|---|
| Combinação | Não | 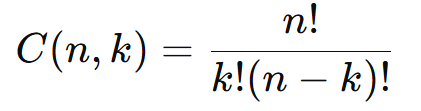 |
| Arranjo Simples | Sim |  |
Passo a Passo para Resolver Combinações Simples
- Identifique os valores de n e k:
Determine o número total de elementos (n) e quantos elementos serão escolhidos (k). - Verifique se a ordem importa:
Se não, utilize a fórmula da combinação simples. - Aplique a fórmula:
Substitua os valores na fórmula C(n,k) = n!/k!(n−k)! - Calcule os fatoriais e simplifique.
👉Entre no nosso canal do WhatsApp
📘 Todas as fórmulas de matemática em um só lugar! Baixe agora nosso eBook gratuito
Exemplos Resolvidos
Exemplo 2: Escolha de Livros
Em uma biblioteca com 8 livros, queremos escolher 3 para levar para casa. Quantas combinações diferentes podem ser feitas?
Solução:
- Total de livros (n): 8.
- Número de livros a escolher (k): 3.
- Aplique a fórmula:
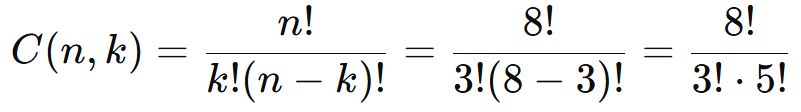
Expanda os fatoriais:
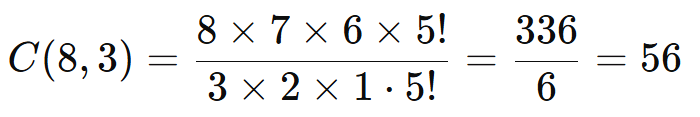
Resposta: Podemos escolher os livros de 56 maneiras diferentes.
Exemplo 3: Combinação de Frutas
Quantas combinações diferentes de 4 frutas podem ser feitas a partir de um cesto com 10 frutas diferentes?
Solução:
- Total de frutas (n): 10.
- Número de frutas a escolher (k): 4.
- Aplique a fórmula:
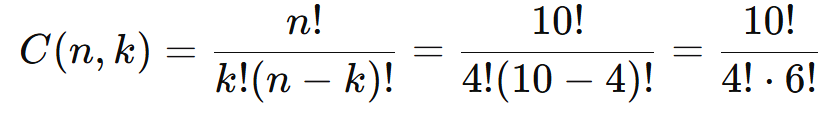
Expanda os fatoriais:
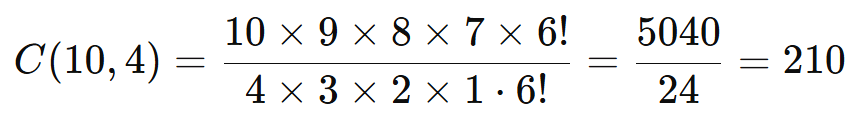
Resposta: Existem 210 combinações possíveis.
Aplicações Práticas da Combinação Simples
A combinação simples tem aplicações amplas em várias áreas da matemática e do dia a dia:
- Pesquisa e Estatística:
Selecionar amostras de dados para análise. - Planejamento de Grupos:
Formar equipes ou comitês em organizações. - Loterias e Jogos:
Calcular as chances de ganhar ao escolher números. - Ciência e Tecnologia:
Analisar combinações de elementos em experimentos. - Educação:
Criar conjuntos de questões em avaliações.
Resumo
A combinação simples é uma ferramenta essencial da análise combinatória, usada para calcular o número de maneiras de selecionar elementos de um conjunto sem se preocupar com a ordem. Sua fórmula, C(n,k)=n!/k!(n−k)!, é direta e eficiente, permitindo resolver problemas rapidamente.
Com exemplos práticos e exercícios resolvidos, você agora está preparado para aplicar esse conceito em situações acadêmicas e do dia a dia. Continue praticando para dominar completamente o tema e explorar outras possibilidades da análise combinatória!