Como Calcular o Determinante de uma Matriz (2 × 2)
Considere uma matriz (2 × 2) genérica da forma:
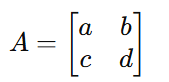
O determinante dessa matriz, indicado por det(A) ou |A|, é dado pela seguinte fórmula:
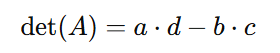
Ou seja, multiplicamos os elementos da diagonal principal (de cima à esquerda para baixo à direita) e subtraímos o produto dos elementos da diagonal secundária (de cima à direita para baixo à esquerda).
Exemplo Prático
Vamos calcular o determinante da matriz abaixo:
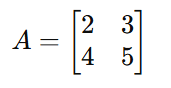
Passo 1: Multiplique os Elementos da Diagonal Principal
A diagonal principal é formada pelos elementos (2) e (5), então:
2⋅5 = 10
Passo 2: Multiplique os Elementos da Diagonal Secundária
A diagonal secundária é formada pelos elementos (3) e (4), então:
3⋅4 = 12
Passo 3: Subtraia os Valores Calculados
Agora, subtraímos o resultado da diagonal secundária do resultado da diagonal principal:

Portanto, o determinante da matriz (A) é -2.
Como Calcular o Determinante de uma Matriz (3 × 3) Usando a Regra de Sarrus
Calcular determinantes é uma operação fundamental na Álgebra Linear e tem várias aplicações, desde a resolução de sistemas lineares até o cálculo de volumes e áreas. Para matrizes de ordem (3 ×3), o método da Regra de Sarrus é uma técnica prática que permite obter o determinante de forma rápida e direta, sem a necessidade de expansões por cofatores. Neste artigo, vamos entender o passo a passo da Regra de Sarrus e aplicá-la a exemplos para garantir um entendimento completo.
1. O Que é o Determinante de uma Matriz?
O determinante é um valor numérico associado a uma matriz quadrada (mesmo número de linhas e colunas), que fornece informações sobre várias propriedades dessa matriz, como a existência ou não de uma inversa. O determinante de uma matriz (3 \times 3) é especialmente útil, pois aparece em contextos como:
- Solução de sistemas lineares,
- Transformações geométricas,
- Cálculos de áreas e volumes.
Quando o determinante de uma matriz é zero, dizemos que ela é singular, o que significa que ela não possui uma inversa.
2. Definindo a Regra de Sarrus
A Regra de Sarrus é um método prático para encontrar o determinante de uma matriz (3 × 3) com a seguinte estrutura:
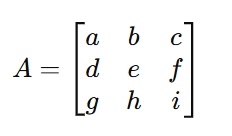
Para aplicar a Regra de Sarrus, realizamos os seguintes passos:
- Repita as duas primeiras colunas ao lado da matriz original para facilitar a identificação das diagonais.
- Multiplique os elementos das diagonais principais (da esquerda para a direita) e some esses produtos.
- Multiplique os elementos das diagonais secundárias (da direita para a esquerda) e some esses produtos.
- Subtraia a soma dos produtos das diagonais secundárias da soma dos produtos das diagonais principais.
3. Passo a Passo da Regra de Sarrus
Vamos ilustrar o cálculo usando a matriz genérica ( A ):
Escreva a Matriz com Colunas Repetidas
Comece escrevendo a matriz e repetindo as duas primeiras colunas ao lado, assim: [
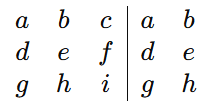
Diagonais Principais
As diagonais principais são as que vão da esquerda para a direita, formando três produtos:

Some esses três produtos para obter o valor das diagonais principais.
- Diagonais Secundárias
As diagonais secundárias são as que vão da direita para a esquerda, formando três produtos:
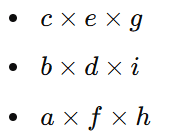
Some esses três produtos para obter o valor das diagonais secundárias.
Subtraia os Valores
O determinante será dado pela diferença entre as somas das diagonais principais e das diagonais secundárias:
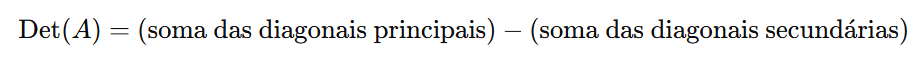
4. Exemplo Prático
Vamos aplicar a Regra de Sarrus para encontrar o determinante da matriz:
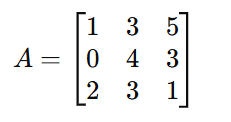
Passo 1: Escreva a Matriz com Colunas Repetidas
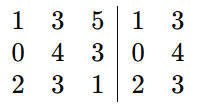
Passo 2: Calcule as Diagonais Principais
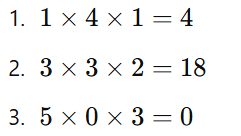
Soma das diagonais principais:
4 + 18 + 0 = 22
Passo 3: Calcule as Diagonais Secundárias
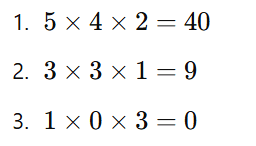
Soma das diagonais secundárias:
40 + 9 + 0 = 49
Passo 4: Calcule o Determinante
Subtraia a soma das diagonais secundárias da soma das diagonais principais:
Det(A) = 22 – 49 = -27
Portanto, o determinante da matriz ( A ) é -27.
5. Conclusão
A Regra de Sarrus é uma ferramenta matemática útil e direta para calcular o determinante de matrizes (3 × 3). Para matrizes maiores, essa regra não se aplica, e é necessário recorrer a métodos mais complexos, como a expansão por cofatores. Entretanto, em matrizes de ordem 3, a Regra de Sarrus facilita o cálculo e reduz a chance de erro, já que permite organizar os cálculos visualmente.
Se você precisar calcular o determinante de uma matriz (3 × 3) de maneira rápida, a Regra de Sarrus é um método excelente para utilizar!
Método Prático para a Regra de Sarrus


























