Conjuntos na Matemática: Conceitos, Tipos e Exemplos Práticos

Os conjuntos são uma das bases fundamentais da matemática, servindo como alicerce para diversas áreas, como a lógica, a álgebra e a teoria dos números. Em termos simples, um conjunto é uma coleção bem definida de elementos, sejam eles números, objetos ou até mesmo ideias. Apesar de sua definição inicial parecer simples, o estudo dos conjuntos abre portas para uma compreensão mais profunda de conceitos matemáticos e aplicações práticas no dia a dia. Neste artigo, vamos explorar o que são conjuntos, suas representações, os tipos especiais como o conjunto vazio e o conjunto universo, além de exemplos que ilustram sua importância.

Conjunto Vazio

O conjunto vazio não contém nenhum elemento e é representado por { } ou Ø.
Exemplo: O conjunto dos números naturais menores que zero é vazio, pois não há números naturais negativos.

Conjunto Universo

O conjunto universo inclui todos os elementos de um contexto ou problema, sendo representado pela letra U.
Exemplo: Em um problema escolar, o conjunto universo pode ser o grupo de todos os alunos matriculados na escola.

Conjunto Unitário

O conjunto unitário possui exatamente um único elemento, representado por {a}.
Exemplo: O conjunto {5} é unitário, pois contém apenas o número 5.

A Relação de Pertinência: Pertence e Não Pertence

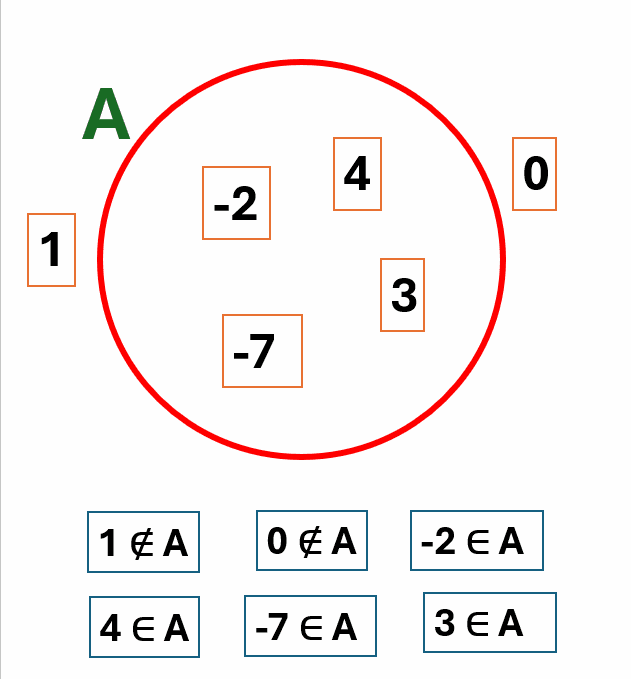
Um conjunto é uma coleção de elementos, como números ou objetos. Quando um elemento faz parte de um conjunto, dizemos que ele pertence ao conjunto (usando o símbolo ∈). Se não faz parte, ele não pertence ao conjunto (usando ∉).

Exemplo 1: Se o conjunto A = {2, 4, 6, 8}, então 4 ∈ A (4 pertence a A) e 5 ∉ A (5 não pertence a A).

Exemplo 2: Considere o conjunto B = {a, e, i, o, u}, que representa as vogais da língua portuguesa.

A letra e é uma vogal, então e ∈ B (e pertence a B).
A letra m não é uma vogal, então m ∉ B (m não pertence a B).

Exemplo 3: Suponha que o conjunto C = {1, 3, 5, 7, 9}, que contém números ímpares menores que 10.

O número 7 está no conjunto, então 7 ∈ C (7 pertence a C).
O número 2 não é ímpar, então 2 ∉ C (2 não pertence a C).

Conjuntos Matemática 1 ano
Tipos de conjuntos
Conjuntos numéricos
Conjuntos Matemática 1 ano ensino médio
Conjunto complementar
Conjunto universo
Operações com conjuntos
Representação de conjuntos

Relações entre Conjuntos: Contém ou Está Contido

Quando estudamos conjuntos, é importante entender como eles se relacionam entre si. Duas das relações mais comuns são “contém” e “está contido”. Esses conceitos nos ajudam a visualizar e organizar conjuntos dentro de outros conjuntos.

1. Está Contido (⊂)

Quando dizemos que um conjunto está contido em outro, queremos dizer que todos os elementos do primeiro conjunto estão dentro do segundo conjunto. O símbolo que usamos para representar isso é ⊂.

Exemplo 1:

Conjunto A: Vamos definir A={1, 2, 3, 4, 5}
Conjunto B: Agora, considere B={2, 3, 4}

Aqui, todos os elementos de B (ou seja, 2, 3 e 4) estão dentro do conjunto A. Portanto, podemos dizer que B está contido em A e escrevemos

B ⊂ A.

Exemplo 2:

Conjunto C: C={a, b, c}
Conjunto D: D={a, b}

Como todos os elementos de D estão dentro de C, dizemos que D ⊂ C (D está contido em C).

2. Contém (⊃)

Por outro lado, quando dizemos que um conjunto contém outro, estamos afirmando que o segundo conjunto é um subconjunto do primeiro. Em outras palavras, todos os elementos do segundo conjunto estão presentes no primeiro. O símbolo usado para isso é ⊃.

Exemplo 1:

Conjunto A: A={1, 2, 3, 4, 5}
Conjunto B: B={2, 3, 4}

Neste caso, A contém B porque todos os elementos de B estão dentro de A. Podemos escrever A ⊃ B.

Conjunto C: C={a, b, c}
Conjunto D: D={a, b}

Aqui, C ⊃ D, significando que C contém D, porque todos os elementos de D estão em C.

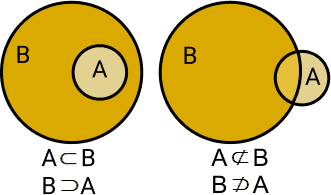
Resumindo:

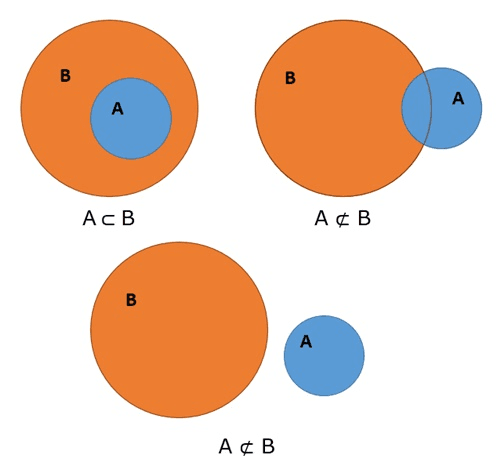
Está Contido (⊂): Todos os elementos de um conjunto estão dentro de outro. Exemplo: B ⊂ A.
Contém (⊃): Um conjunto tem todos os elementos de outro dentro dele. Exemplo: A ⊃ B.

Esses conceitos são fundamentais na matemática para organizar e entender como diferentes grupos de elementos se relacionam entre si. Eles são especialmente úteis quando lidamos com conjuntos complexos, permitindo-nos visualizar hierarquias e relações de inclusão.

Conjuntos Iguais

Na matemática, dizemos que dois conjuntos são iguais quando ambos contêm exatamente os mesmos elementos, independentemente da ordem em que esses elementos são listados. A igualdade entre conjuntos é indicada pelo símbolo =.

Definição:

Dois conjuntos A e B são iguais se e somente se:

Todo elemento de A está em B.
Todo elemento de B está em A.

Formalmente, podemos escrever isso como:

A = B ⟺ (∀x (x ∈ A ⇒ x ∈ B) e ∀x (x ∈ B ⇒ x ∈ A))

Em palavras simples: Se cada elemento de A está em B e vice-versa, então A e B são iguais.

Exemplo 1:

Conjunto A: A={1, 2, 3}
Conjunto B: B={3, 2, 1}

Apesar da ordem dos elementos ser diferente, os conjuntos A e B são iguais porque contêm exatamente os mesmos elementos. Portanto, podemos dizer que A = B.

Exemplo 2:

Conjunto C: C={a, b, c}
Conjunto D: D={c, b, a}

Novamente, a ordem dos elementos não importa; C e D são iguais porque têm os mesmos elementos. Assim, C = D.

Exemplo 3:

Conjunto E: E={1, 2, 3}
Conjunto F: F={1, 2, 4}

Aqui, E e F não são iguais porque o elemento 3 está em E mas não em F, e o elemento 4 está em F mas não em E. Portanto, E ≠ F.

Resumo:

Dois conjuntos são iguais quando têm exatamente os mesmos elementos, sem importar a ordem ou a forma como esses elementos são listados. Isso é fundamental para garantir que diferentes representações de conjuntos sejam tratadas de maneira consistente na matemática.

União de Conjuntos (∪)

A operação de união entre dois conjuntos consiste em formar um novo conjunto que contém todos os elementos pertencentes a pelo menos um dos conjuntos originais. A união é representada pelo símbolo ∪.

Definição

Sejam A e B dois conjuntos, a união A∪B é o conjunto formado por todos os elementos que pertencem a A, B, ou a ambos. Em termos matemáticos:

A∪B = {x ∣ x∈A ou x∈B}

Exemplo

Considere os conjuntos:

A = {1, 2, 3, 5, 6, 8}
B = {1, 2, 4, 7, 8}

A união A∪B resulta no conjunto: A∪B ={1, 2, 3, 4, 5, 6, 7, 8}

Representação Visual

No diagrama de Venn, a união de dois conjuntos é representada pela área combinada de ambos os círculos, incluindo os elementos que aparecem em apenas um conjunto e os que aparecem em ambos.

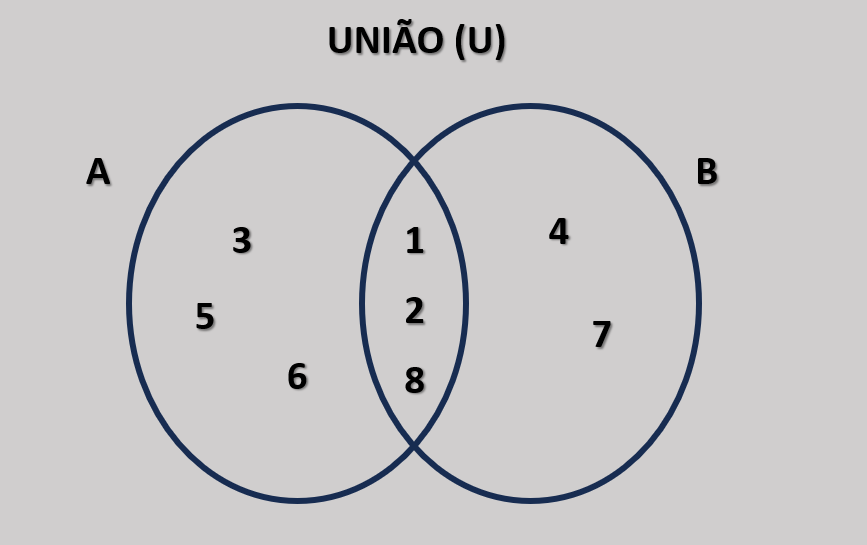
A operação de união é uma ferramenta fundamental na teoria dos conjuntos, sendo amplamente utilizada em problemas que envolvem a combinação de informações ou agrupamento de elementos distintos.

Interseção de Conjuntos (∩)

A operação de interseção entre dois conjuntos resulta em um novo conjunto formado apenas pelos elementos que são comuns a ambos os conjuntos. A interseção é representada pelo símbolo ∩.

Definição

Sejam A e B dois conjuntos, a interseção A∩B é o conjunto formado pelos elementos que pertencem simultaneamente a A e B. Em termos matemáticos:

A∩B = {x ∣ x∈A e x∈B}

Exemplo

Considere os conjuntos:

A = {1, 2, 3, 5, 6, 8}
B = {1, 2, 4, 7, 8}

A interseção A∩B resulta no conjunto: A∩B = {1, 2, 8}

Representação Visual

No diagrama de Venn, a interseção de dois conjuntos é representada pela área em que os círculos de A e B se sobrepõem. Essa área destaca os elementos que estão presentes em ambos os conjuntos.

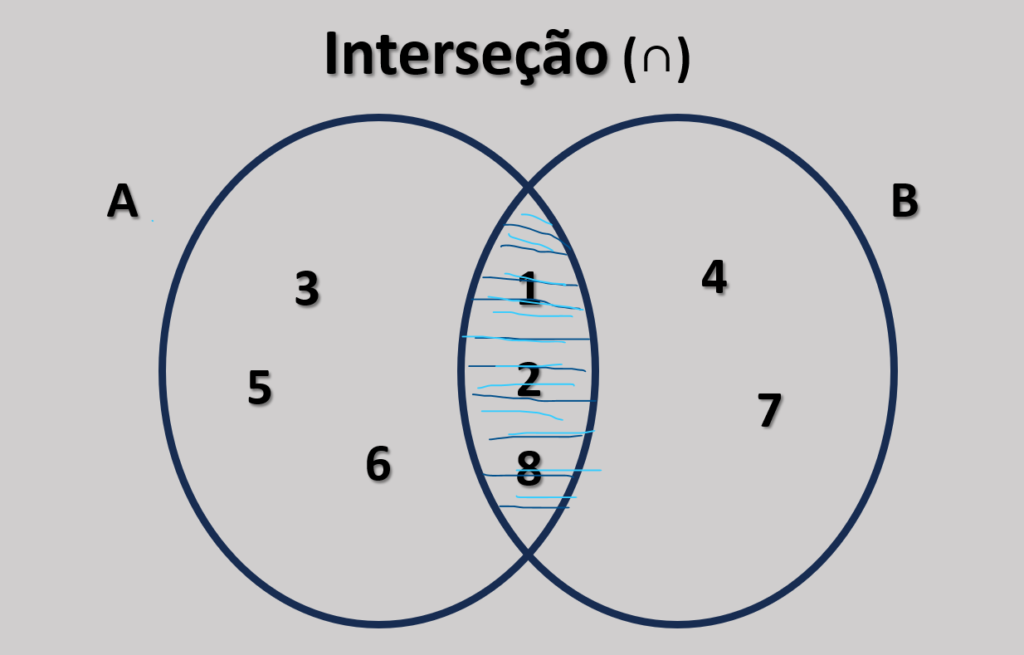
A interseção é uma operação central na teoria dos conjuntos, sendo usada para identificar elementos compartilhados em diferentes agrupamentos ou categorias.

Diferença de Conjuntos (-)

A operação de diferença entre dois conjuntos resulta em um novo conjunto formado pelos elementos que pertencem ao primeiro conjunto, mas não ao segundo. A diferença é representada pelo símbolo −.

Definição

Sejam A e B dois conjuntos, a diferença A – B é o conjunto dos elementos que pertencem a A, mas não pertencem a B. Em termos matemáticos:

A − B={x ∣ x∈A e x∉B}

Exemplo

Considere os conjuntos:

A = {1, 2, 3, 5, 6, 8}
B = {1, 2, 4, 7, 8}

A diferença A – B resulta no conjunto: A – B = {3, 5, 6}

Representação Visual

No diagrama de Venn, a diferença A – B é representada pela parte do círculo de A que não se sobrepõe ao círculo de B. Esta região destaca os elementos exclusivos de AA, excluindo aqueles que também pertencem a B.

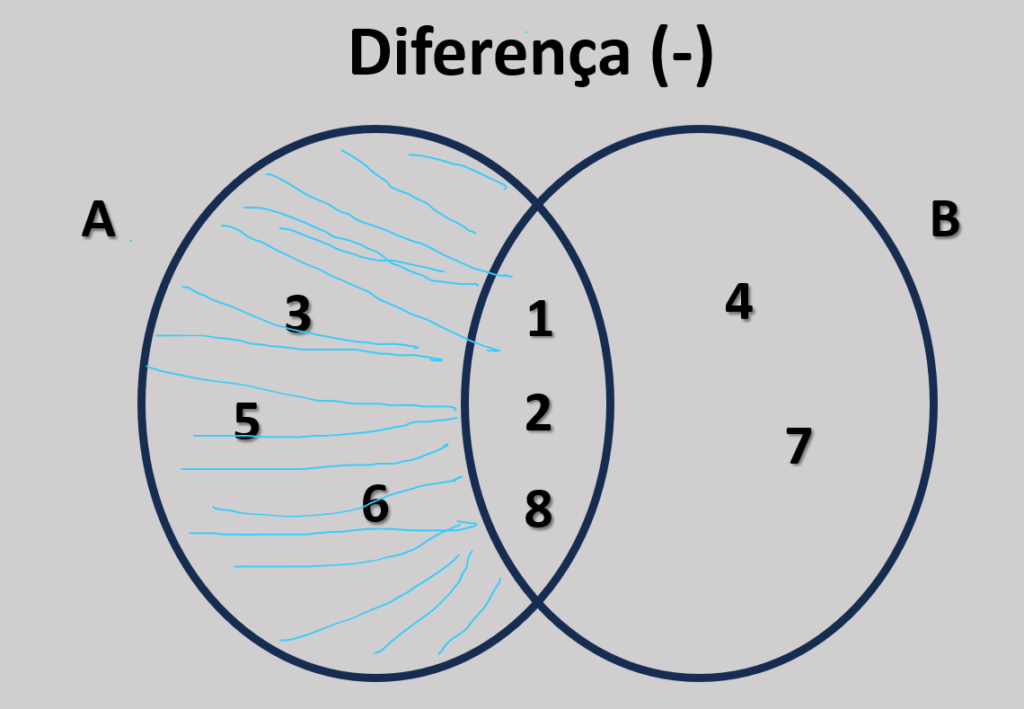
A operação de diferença é essencial para identificar elementos que pertencem exclusivamente a um conjunto, sendo amplamente utilizada em classificações e análises de dados.

Complemento de Conjuntos

O complemento de um conjunto consiste nos elementos que pertencem a um conjunto maior (chamado conjunto universo), mas que não pertencem ao subconjunto especificado. A operação de complemento é representada por C ou A – B, dependendo do contexto.

Definição

Se B é um subconjunto de A (B ⊆ A), o complemento de B em relação a A (C_A^B) é o conjunto dos elementos que pertencem a A, mas não pertencem a BB. Matematicamente:

C_A^B = A − B = {x ∣ x∈A e x∉B}

Exemplo

Considere os conjuntos:

A = {1, 2, 3, 5, 6, 8}
B = {1, 2, 3}

O complemento de B em relação a A é:

C_A^B = A − B = {5, 6, 8}

Representação Visual

No diagrama de Venn, o complemento de B em relação a A é representado pela área de A que não está ocupada por B. Essa região destaca os elementos que pertencem somente a A, excluindo os que estão em B.

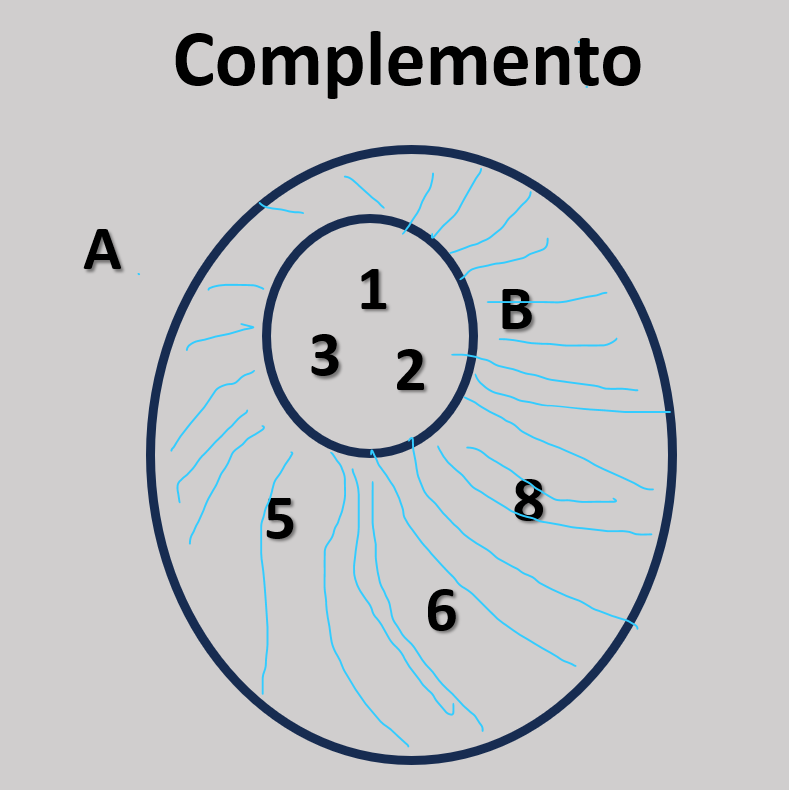
Aplicação

O complemento é amplamente utilizado para identificar elementos que não atendem a determinados critérios, especialmente em problemas de classificação, lógica e probabilidade. É uma ferramenta importante para análise e organização de dados.

Conjunto das Partes

O conjunto das partes de um conjunto A é o conjunto que contém todos os subconjuntos possíveis de A. Isso inclui o próprio conjunto A, o conjunto vazio ∅, e todos os subconjuntos formados pelos elementos de A.

O conjunto das partes de A é denotado por P(A).

Definição Formal:

Se A é um conjunto, então o conjunto das partes de A, denotado por P(A), é definido como: P(A) = {X ∣ X ⊂ A}.

Isso significa que P(A) é o conjunto de todos os subconjuntos X de A.