Você já ouviu a expressão “sem tirar o lápis do papel”? Pois é exatamente essa a ideia por trás da continuidade de uma função. Neste artigo, vamos te explicar de forma clara o que significa uma função ser contínua, quando ela deixa de ser, quais os tipos de descontinuidade, além de mostrar exemplos resolvidos passo a passo.
✅ O que é continuidade de uma função?
Uma função é contínua em um ponto x = a quando não há interrupções no gráfico da função naquele ponto. Intuitivamente, isso significa que conseguimos desenhar o gráfico sem levantar o lápis do papel.
📌 Definição formal de continuidade em um ponto
A função f(x) é contínua em x = a se e somente se as três condições a seguir forem satisfeitas:
- f(a) está definida
- limx→a f(x) existe
- limx→a f(x) = f(a)
Se qualquer uma dessas condições falhar, a função será descontínua em x = a.
📈 Continuidade em um intervalo
Uma função é dita contínua em um intervalo quando ela é contínua em todos os pontos desse intervalo. Por exemplo:
f(x) = x²é contínua em todoℝf(x) = 1/xnão é contínua emx = 0
🚧 Tipos de descontinuidade
🔸 Descontinuidade Removível
O limite existe, mas o valor da função é diferente ou não está definido.
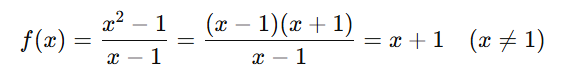
Neste caso, há um buraco em x = 1, que pode ser “removido” se definirmos f(1) = 2.
🔸 Descontinuidade por Salto
O limite à esquerda e à direita existem, mas são diferentes.
🔸 Descontinuidade Infinita
A função tende ao infinito em um ponto. Exemplo:
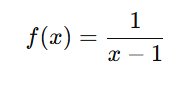
🧠 Exemplos resolvidos
✅ Exemplo 1 – Função polinomial
Função: f(x) = x² + 5x - 2
Conclusão: Toda função polinomial é contínua em todo seu domínio. Portanto, f(x) é contínua para todos os reais.
✅ Exemplo 2 – Função definida por partes
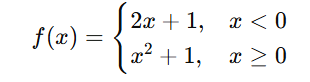
Pergunta: A função é contínua em x = 0?
- f(0) = 0² + 1 = 1
- limx→0⁻ = 2(0) + 1 = 1
- limx→0⁺ = 0² + 1 = 1
Conclusão: A função é contínua em x = 0.
✅ Exemplo 3 – Encontrar valor para garantir continuidade
Simplificação: (x² – 9)/(x – 3) = x + 3, para x ≠ 3
Limite: limx→3 f(x) = 6
Para garantir continuidade: basta definir k = 6
🎯 Conclusão
Entender a continuidade de uma função é essencial para o estudo do Cálculo. Ela nos permite compreender o comportamento de gráficos, limites, derivadas e integrais com mais profundidade.
Se você gostou deste conteúdo, compartilhe com seus colegas e continue explorando outros temas importantes da matemática!
