O determinante é uma função matemática que atribui um valor numérico a uma matriz quadrada, proporcionando informações cruciais sobre as propriedades da matriz, como se ela é invertível ou não. Além disso, o determinante é essencial em diversas áreas da matemática, como a solução de sistemas lineares, o cálculo de volumes em geometria e a análise de transformações lineares.
Determinante de uma Matriz 2×2
O cálculo do determinante de uma matriz 2×2 é bastante direto e serve como base para o entendimento de determinantes de matrizes de ordens maiores. Para uma matriz
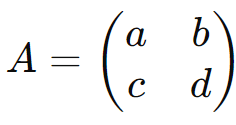
o determinante é dado por:
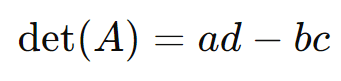
Este valor pode ser interpretado geometricamente como a área do paralelogramo formado pelos vetores coluna da matriz.
Exemplo:
Considere a matriz
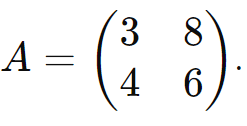
O determinante de ( A ) é calculado como:
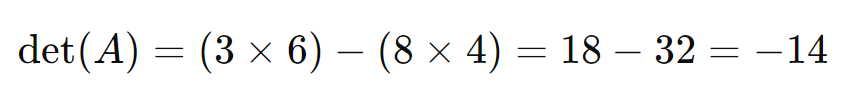
Neste caso, o determinante é (-14), o que indica que a matriz é invertível e que o paralelogramo formado tem uma área com valor absoluto de 14 unidades quadradas.
Determinante de uma Matriz 3×3
O cálculo do determinante de uma matriz 3×3 é um pouco mais complexo e envolve a expansão pela regra de Sarrus ou o co-fator. Para uma matriz
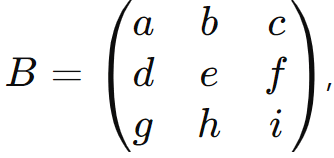
o determinante pode ser calculado por:
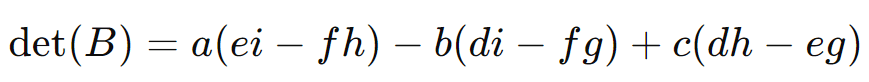
Esse processo pode ser visualizado como a soma de produtos de diagonais principais e secundárias, subtraindo-se os resultados correspondentes.
Exemplo:
Considere a matriz
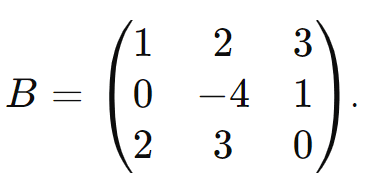
O determinante de ( B ) é:
det(B) = 1((-4 x 0) – (1 x 3)) – 2((0 x 0) – (1 x 2)) + 3((0 x 3) – (-4 x 2))
det(B) = 1(0 – 3) – 2(0 – 2) + 3(0 + 8) = -3 + 4 + 24 = 25
O determinante da matriz ( B ) é 25, indicando que a matriz é invertível e que a transformação associada a essa matriz preserva a orientação e a escala.
Determinante de Matrizes Maiores
Para matrizes de ordem superior a 3×3, o cálculo do determinante é geralmente realizado através da expansão por co-fatores ou de métodos numéricos, como a eliminação de Gauss.
Expansão por Co-Fatores
O método de co-fatores generaliza o cálculo de determinantes para qualquer matriz quadrada ( n x n ). Para uma matriz ( C ) de ordem ( 4 x 4 ) ou maior, o determinante é calculado expandindo em relação a uma linha ou coluna, multiplicando cada elemento dessa linha ou coluna pelo determinante do menor complementar (a matriz obtida ao remover a linha e a coluna do elemento) e aplicando um sinal alternante.
Exemplo:
Para uma matriz
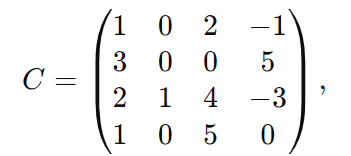
o determinante pode ser calculado expandindo pela primeira linha:

Cada um desses subdeterminantes pode ser calculado usando o mesmo método até chegar a determinantes de matrizes 2×2.
Método de Eliminação de Gauss
Para matrizes muito grandes, o método de eliminação de Gauss é usado para simplificar a matriz a uma forma triangular superior, onde o determinante é simplesmente o produto dos elementos na diagonal principal. Esse método é muito mais eficiente para matrizes de alta ordem.
Exemplo:
Dada uma matriz

aplicando a eliminação de Gauss para triangular:
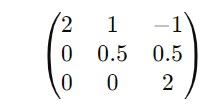
O determinante é o produto dos elementos da diagonal principal:
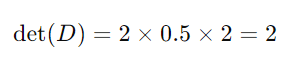
Propriedades dos Determinantes
O determinante possui diversas propriedades importantes que são úteis na manipulação e simplificação de cálculos. Abaixo, estão algumas das principais:
- Determinante da Matriz Transposta: O determinante de uma matriz transposta é igual ao determinante da matriz original. Ou seja, se ( A ) é uma matriz, então:
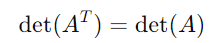
- Produto de Matrizes: O determinante do produto de duas matrizes é igual ao produto dos determinantes das matrizes. Para matrizes ( A ) e ( B ), temos:
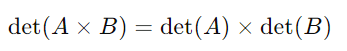
- Determinante da Matriz Inversa: O determinante da matriz inversa é o inverso do determinante da matriz original. Para uma matriz ( A ) invertível, vale:
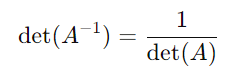
- Matriz Diagonal: O determinante de uma matriz diagonal é o produto dos elementos da diagonal principal. Para uma matriz diagonal ( D ):
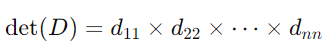
- Troca de Linhas: Trocar duas linhas (ou colunas) de uma matriz inverte o sinal do determinante. Se ( B ) é a matriz resultante da troca de duas linhas de ( A ), então:
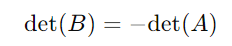
- Linha ou Coluna Nula: Se uma matriz possui uma linha ou coluna composta apenas por zeros, seu determinante é igual a zero.
- Linha ou Coluna Proporcional: Se duas linhas ou colunas de uma matriz são proporcionais, o determinante da matriz é zero.
- Adição de Múltiplo de Linha ou Coluna: Adicionar a uma linha (ou coluna) de uma matriz um múltiplo de outra linha (ou coluna) não altera o determinante.
Conclusão
O determinante é uma ferramenta poderosa que proporciona insights profundos sobre as propriedades das matrizes e as transformações que elas representam. Compreender o cálculo de determinantes para matrizes de diferentes ordens é essencial para a aplicação em sistemas lineares, geometria, análise e muito mais. Seja através de métodos diretos para matrizes pequenas ou técnicas mais avançadas para matrizes maiores, o determinante continua sendo um conceito central na matemática. Além disso, o domínio das propriedades dos determinantes facilita significativamente a resolução de problemas complexos envolvendo matrizes.
Leia também
Matriz: o que é, tipos, operações, exercícios
Sistemas Lineares Descomplicado: Guia Completo para Solução e Interpretação
Entendendo o Binômio de Newton













