Divisão de polinômio por polinômio

Você já conhece o algoritmo da divisão de números naturais.

Agora, estudaremos a divisão de polinômios, cujo algoritmo (dispositivo prático) é semelhante àquele da divisão de números naturais.

Dados dois polinômios A e B na mesma variável, com B ≠ 0, é sempre possível encontrar os polinômios Q e R tais que:

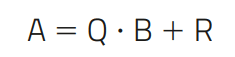
sendo grau de R < grau de B (ou R = 0, na divisão exata).

• Q é quociente da divisão de A por B.
• R é resto da divisão de A por B.
• A é dividendo.
• B é divisor

Dividir um polinômio A por outro polinômio B significa determinar o quociente Q e o resto R dessa divisão.

Nos exemplos a seguir, mostraremos como se efetua a divisão de polinômios.

Exemplo 01 – Vamos dividir A = 12x² + 23x + 13 por B = 4x + 1.

1 – Dividimos o termo de maior grau de A (12x²) pelo termo de maior grau de B (4x) e colocamos o resultado no quociente:

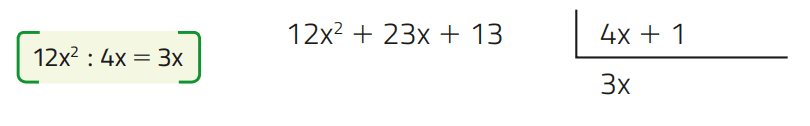
2 – Multiplicamos o quociente obtido (3x) pelo divisor e subtraímos o resultado do dividendo. Obtemos, assim, um resto parcial:

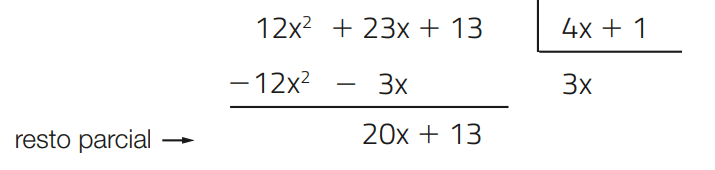
3 – Dividimos o termo de maior grau do resto parcial (20x) pelo termo de maior grau do divisor (4x). O resultado é um termo que acrescentamos ao quociente:

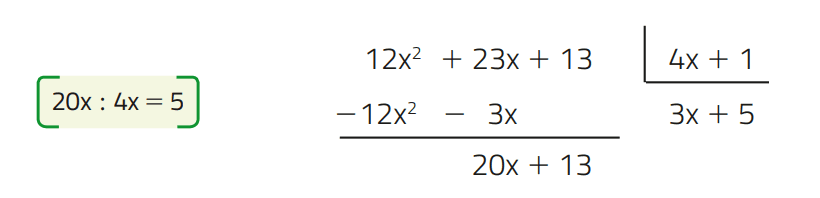
4 – Multiplicamos esse termo (5) pelo divisor e subtraímos o resultado do resto anterior:

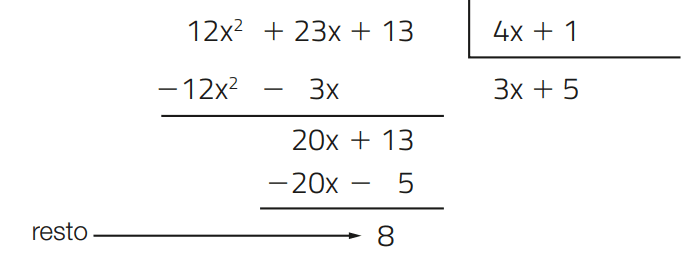
O resto obtido tem grau menor que o do divisor. Então, o quociente é Q = 3x + 5 e o resto é R = 8.
Finalizamos a divisão quando encontramos um resto igual a zero (R = 0) ou um resto que é um polinômio de grau menor do que o grau do divisor.

Exemplo 02 – Vamos dividir A = 2x³ + 9x² + 1 por B = 2x² + x.

Como está faltando o termo em x no polinômio A, indicamos esse termo por 0x. Temos:

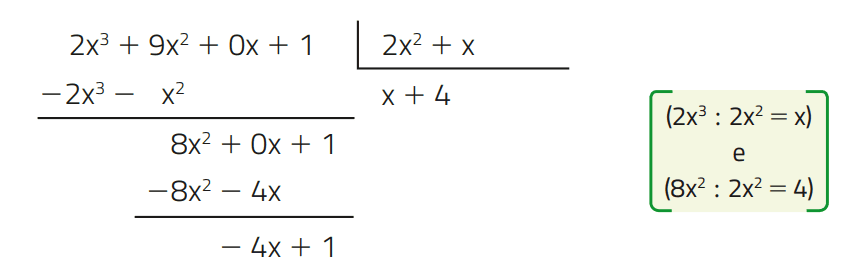
O quociente é Q = x + 4 e o resto é R = -4x + 1.

Assim, lembrando que A = Q x B + R, podemos escrever:

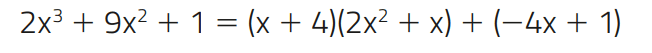
Exemplo 03 –Vamos dividir A = x⁴ – 2x³ – 14x² – 5x por B = x² + 3x + 1.

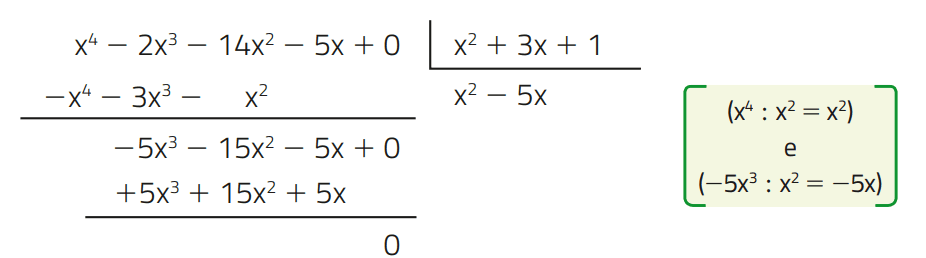
Então, o quociente é Q = x² – 5x e o resto é R = 0. Como a divisão é exata, o polinômio A é divisível pelo polinômio B.

Nesse caso, temos:

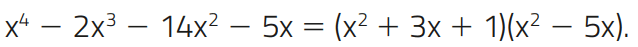
Lista de Exercício Divisão de polinômio por polinômio

01 – Qual é o polinômio que, dividido por x² + 2, dá quociente x + 2 e resto x – 2?
a) x³ + x² + 3x + 2
b) x³ + 2x² + 2x + 2
c) x³ + 2x² + 3x + 2
d) x³ + 2x² + 3x

Ver Solução

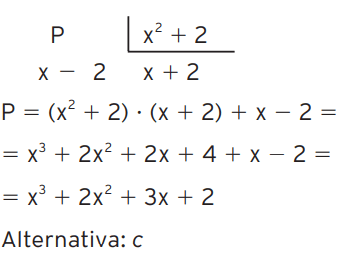
02 – Ao dividir x³ + 1 por x² + 1, encontramos resto:
a) 0
b) x
c) x + 1
d) -x + 1

Ver Solução

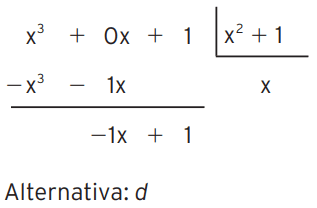
03 – Qual é o polinômio que, dividido por B = 3x² + 4x – 1, dá quociente Q = x + 1 e resto R = -3x + 1?

Ver Solução

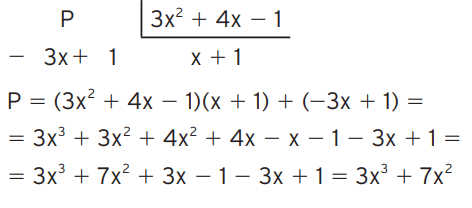
04 – Por qual monômio devemos multiplicar 4xy² para obter como produto 20x⁴y⁴?

Ver Solução

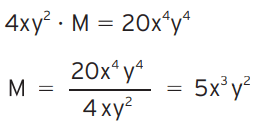
Exercícios 01 de Cálculo Algébrico com Solução: Expressões e Operações com Polinômios