Equações Logarítmicas: Um Guia Completo

Introdução

As equações logarítmicas são equações que envolvem logaritmos e desempenham um papel crucial em muitos campos da matemática e ciências aplicadas. Elas surgem em situações que envolvem crescimento exponencial, escalas logarítmicas e em várias outras áreas, como finanças, física e biologia. Este artigo abordará a definição, as técnicas de resolução, as propriedades relevantes e exemplos de equações logarítmicas, oferecendo uma visão abrangente do tema.

Definição de Equação Logarítmica

Uma equação logarítmica é uma equação que envolve uma ou mais expressões logarítmicas. A forma geral de uma equação logarítmica é:

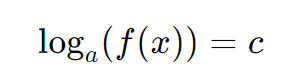
onde a é a base do logaritmo (com a > 0 e a ≠ 1), f(x) é uma função de x, e c é uma constante real. O objetivo ao resolver uma equação logarítmica é encontrar o valor ou os valores de x que satisfazem a equação.

Condições de Existência

Antes de resolver uma equação logarítmica, é essencial considerar as condições de existência. Para que log⁡_a(f(x)) esteja definida, a função f(x) deve ser positiva:

f(x)>0

Essa condição garante que o argumento do logaritmo seja válido, já que o logaritmo de um número não positivo não está definido no conjunto dos números reais.

Métodos de Resolução de Equações Logarítmicas

Para resolver uma equação logarítmica, podemos seguir os seguintes passos:

1. Verificação das Condições de Existência:
   • Primeiramente, determine o domínio da função, garantindo que o argumento do logaritmo seja positivo.
2. Isolamento do Logaritmo:
   • Se possível, isole o logaritmo em um dos lados da equação.
3. Transformação em Equação Exponencial:
   • Utilize a definição de logaritmo para transformar a equação logarítmica em uma equação exponencial. Se log_⁡a(f(x))=c, então f(x)=a^c.
4. Resolução da Equação Resultante:
   • Resolva a equação resultante para encontrar o valor de x.
5. Verificação das Condições de Existência:
   • Verifique se as soluções encontradas atendem às condições de existência estabelecidas no início.

Propriedades Importantes dos Logaritmos

1. Propriedade do Produto: A propriedade do produto dos logaritmos estabelece que o logaritmo de um produto de dois números é igual à soma dos logaritmos desses números, ambos com a mesma base. Em outras palavras, para uma base a, a propriedade pode ser expressa como:

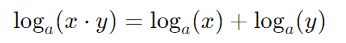
Essa propriedade é útil quando precisamos calcular logaritmos em uma base para a qual não temos uma tabela ou calculadora disponível.

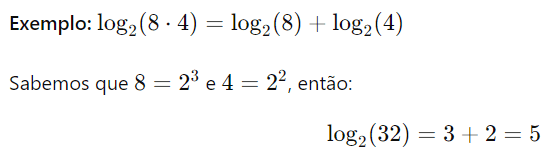
• Propriedade do Quociente: A propriedade do quociente dos logaritmos afirma que o logaritmo de um quociente entre dois números é igual à diferença entre os logaritmos desses números, ambos com a mesma base. Formalmente, para uma base aaa, essa propriedade é expressa como:

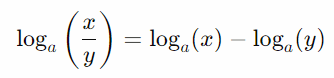
Essa propriedade é útil para simplificar expressões logarítmicas e resolver equações envolvendo divisões.

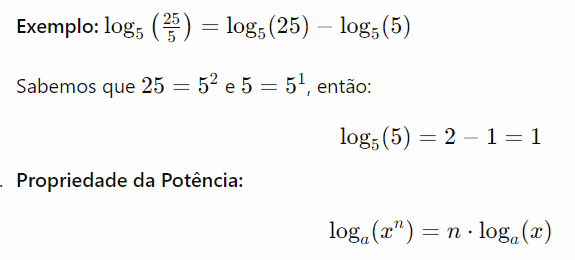
Propriedade da Potência: A propriedade da potência dos logaritmos estabelece que o logaritmo de um número elevado a um expoente é igual ao produto do expoente pelo logaritmo do número, ambos com a mesma base. Em termos formais, para uma base a, essa propriedade é dada por:

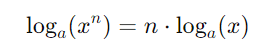
Essa propriedade facilita o processo de simplificação de expressões logarítmicas, especialmente quando lidamos com potências.

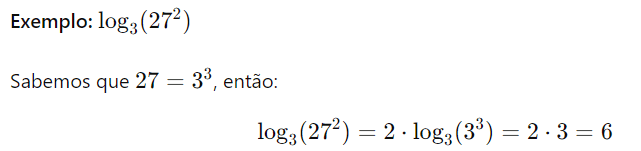
• Propriedade da Raiz: A propriedade da raiz dos logaritmos afirma que o logaritmo de uma raiz n-ésima de um número é igual ao logaritmo desse número dividido por n, ambos com a mesma base. Formalmente, para uma base a, essa propriedade pode ser expressa como:

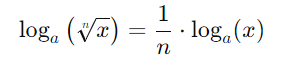
Essa propriedade é útil para simplificar expressões logarítmicas que envolvem raízes.

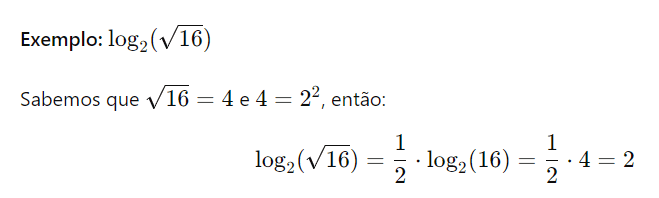
• Mudança de Base: A propriedade da mudança de base dos logaritmos permite calcular o logaritmo de um número em uma base diferente da original. Ela afirma que o logaritmo de um número x na base a pode ser expresso como a razão entre o logaritmo de x e o logaritmo de a em uma nova base b. Formalmente, a propriedade é dada por:

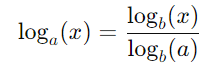
Essa propriedade é útil quando precisamos calcular logaritmos em uma base para a qual não temos uma tabela ou calculadora disponível.

Exemplos Resolvidos de Equações Logarítmicas

Exemplo 1: Resolva a equação log⁡₂(x)=3.

Exemplo 2: Resolva a equação log⁡₃(x+1)=log⁡₃(2x−5).

Exemplo 3: Resolva a equação log⁡₂(x²−4)=3.

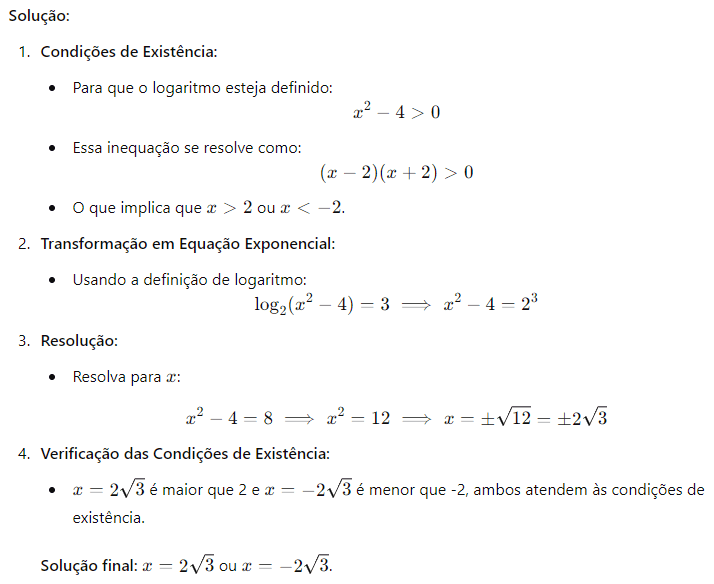
Exemplo 4: Resolva a equação log_⁡0,5(x−2)=−1.

Conclusão

As equações logarítmicas são uma ferramenta poderosa na matemática, permitindo resolver problemas que envolvem crescimento exponencial, escalas logarítmicas, entre outros. Temos também as inequações logarítmicas Dominar as propriedades dos logaritmos e os métodos de resolução dessas equações é essencial para compreender uma ampla gama de aplicações práticas. Com uma abordagem sistemática, incluindo a verificação das condições de existência e a transformação adequada das equações, é possível resolver equações logarítmicas com precisão e eficácia.