As equações trigonométricas são um tipo de equação matemática que envolve funções trigonométricas como seno (sin), cosseno (cos), tangente (tan), entre outras. Essas equações surgem naturalmente em diversos campos, como física, engenharia, astronomia, e até mesmo em problemas do cotidiano que envolvem ângulos e ciclos periódicos. Resolver uma equação trigonométrica significa encontrar todos os valores da variável (geralmente um ângulo) que satisfazem a equação dentro de um determinado intervalo ou em todos os múltiplos possíveis de 2π.
Tipos de Equações Trigonométricas
As equações trigonométricas podem variar em complexidade, desde as mais simples, envolvendo apenas uma função trigonométrica, até aquelas que combinam várias funções diferentes. A seguir, são apresentados os principais tipos de equações trigonométricas.
1. Equações Trigonométricas Simples
Equações simples envolvem diretamente uma única função trigonométrica. Elas são as mais básicas e frequentemente servem como ponto de partida para entender conceitos mais avançados.
Exemplo: sin(x)=1/2
Para resolver essa equação, precisamos determinar os valores de x para os quais o seno é igual a 1/2. Sabemos que:

2. Equações Trigonométricas Quadráticas
Essas equações têm a forma de uma equação quadrática em uma função trigonométrica e podem ser resolvidas utilizando técnicas de fatoração ou a fórmula quadrática.
Exemplo: 2cos2(x)−3cos(x)+1=0
Podemos resolver essa equação fazendo uma substituição y=cos(x), transformando-a em uma equação quadrática:
2y2 − 3y + 1 = 0
Usando a fórmula de Bhaskara, temos:
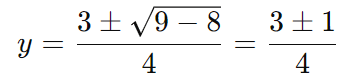
Então, y=1 ou y=1/2. Substituindo de volta cos(x) por y, obtemos:

onde k é um número inteiro.
3. Equações Trigonométricas com Identidades
Algumas equações exigem o uso de identidades trigonométricas, como as identidades de ângulos duplos ou metade, para simplificar e resolver a equação.
Exemplo: sin(2x)=2sin(x)cos(x)
Sabemos que a identidade sin(2x)=2sin(x)cos(x) é verdadeira para todos os valores de x. Portanto, essa equação é uma identidade trigonométrica, e qualquer x é solução.
No entanto, se tivermos uma equação como:
sin(2x)=cos(x)
Precisamos aplicar identidades e manipular a equação para encontrar as soluções de x.
4. Equações com Múltiplas Funções Trigonométricas
Essas equações envolvem mais de uma função trigonométrica e geralmente requerem que uma das funções seja expressa em termos de outra para simplificação.
Exemplo: sin(x)+cos(x)=0
Podemos dividir a equação por cos(x) (assumindo que cos(x)≠0):

Então, as soluções são:
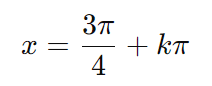
onde k é um número inteiro.
Métodos de Resolução
Para resolver equações trigonométricas, os matemáticos empregam uma variedade de técnicas, dependendo do tipo e da complexidade da equação. Alguns métodos comuns incluem:
- Substituições Trigonométricas: Usar identidades trigonométricas para substituir uma função por outra mais simples.
- Transformação em Equações Algébricas: Transformar a equação trigonométrica em uma equação algébrica através de substituições.
- Fatoração: Fatorar a equação para simplificar e encontrar as raízes.
- Uso de Identidades: Aplicar identidades trigonométricas para reescrever e simplificar a equação.
- Análise Gráfica: Usar gráficos para visualizar as soluções.
Resolução de Equações Trigonométricas: Exercícios Práticos e Soluções Passo a Passo
Exercício 1: Resolva a equação sin(x)=√3/2 para 0 ≤ x < 2π.
Solução: Sabemos que sin(x)=√3/2 ocorre nos ângulos x=π/3 e x=2π/3 dentro de um ciclo 0≤x<2π.
Assim, as soluções no intervalo dado são:

Exercício 2: Resolva a equação 2cos2(x)−5cos(x)+2=0 para 0≤x<2π.
Solução: Primeiro, fazemos a substituição y=cos(x), transformando a equação em uma quadrática:
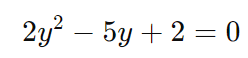
Resolvendo essa equação quadrática:

Isso nos dá:
y=2(descartado porque cos(x) não pode ser maior que 1),
Portanto, cos(x)=1/2. Agora, encontramos os valores de x no intervalo 0≤x<2π onde o cosseno vale 1/2:
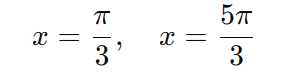
Exercício 3: Resolva a equação sin(2x)=cos(x) para 0≤x<2π.
Solução: Primeiro, usamos a identidade sin(2x)=2sin(x)cos(x), então a equação se torna:
2sin(x)cos(x)=cos(x)
Podemos fatorar a equação:
cos(x)(2sin(x)−1)=0
Isso nos dá duas equações:
- cos(x)=0
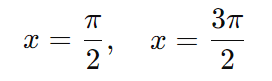
2sin(x)−1=0
sin(x)=1/2
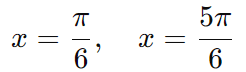
Portanto, as soluções no intervalo 0≤x<2π são:
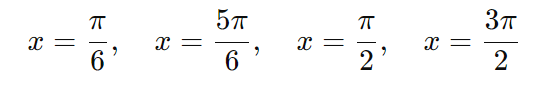
Leia também História da Trigonometria

























