Na teoria das probabilidades, os espaços amostrais equiprováveis desempenham um papel fundamental, especialmente quando lidamos com experimentos aleatórios em que todos os resultados têm a mesma chance de ocorrer. Esses espaços são ideais para analisar situações clássicas, como lançamentos de dados, sorteios de cartas ou qualquer experimento simétrico.
Neste artigo, exploraremos detalhadamente o conceito de espaços amostrais equiprováveis, abordaremos como calcular probabilidades nesses casos e apresentaremos exemplos mais elaborados.

O Que São Espaços Amostrais Equiprováveis?
Um espaço amostral (S) é o conjunto de todos os possíveis resultados de um experimento aleatório. Ele é considerado equiprovável quando cada um de seus elementos tem a mesma probabilidade de ocorrer. Formalmente, se S contém k elementos, a probabilidade de qualquer evento elementar ai ∈ S é dada por:
P(ai) = 1/k, para todo ai ∈ S
Essa característica de equiprobabilidade é comum em experimentos em que não há preferência ou viés, como lançar uma moeda justa, lançar um dado equilibrado ou sortear uma carta de um baralho completo.
Como Calcular a Probabilidade em Espaços Equiprováveis?
Quando SS é equiprovável, a probabilidade de um evento A (um subconjunto de S) é dada pela razão entre o número de elementos favoráveis ao evento (|A|) e o total de elementos no espaço amostral (|S|):

Exemplo 1: Sorteio de Uma Carta no Baralho
Situação: Considere um baralho padrão com 52 cartas.
- Espaço amostral: S={2c, 2o, 2e, …, Kp, Ac, Ao, Ae, Ap} onde os índices c, o, e, p representam os naipes: copas, ouros, espadas e paus.
- Probabilidade de qualquer carta:
Cada carta tem a mesma probabilidade: P(ai) = 1/52, para todo ai ∈ S
Evento A: A carta é de copas
O evento A contém as 13 cartas do naipe de copas: A={2c, 3c, …, Kc, Ac}
Número de elementos favoráveis: |A| = 13.
Probabilidade:
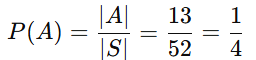
Evento B: A carta é uma dama
O evento B contém 4 cartas, uma dama de cada naipe: B={Qc, Qo, Qe, Qp}
Número de elementos favoráveis: |B| = 4.
Probabilidade:
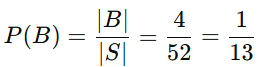
Exemplo 2: Lançamento de Dois Dados
Situação: Considere o lançamento simultâneo de dois dados comuns.
- Espaço amostral:
Cada dado tem 6 faces, então o espaço amostral contém todos os pares ordenados de resultados: S={(1,1),(1,2),…,(6,6)}, ∣S∣ = 36 - Probabilidade de cada resultado:
Cada par tem a mesma probabilidade: P(ai) = 1/36, para todo ai ∈ S
Evento A: A soma dos dois dados é 8
Os pares que resultam em soma 8 são: A={(2,6),(3,5),(4,4),(5,3),(6,2)}
Número de elementos favoráveis: |A| = 5.
Probabilidade:
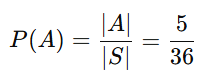
Evento B: O primeiro dado mostra 4
Os pares em que o primeiro dado é 4 são: B={(4,1),(4,2),(4,3),(4,4),(4,5),(4,6)}
Número de elementos favoráveis: |B| = 6.
Probabilidade:
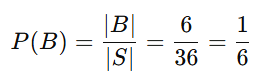
Exemplo 3: Lançamento de Uma Moeda Três Vezes
Situação: Considere o experimento de lançar uma moeda três vezes.
- Espaço amostral: S={CCC, CCT, CTC, CTT, TCC, TCT, TTC, TTT}, ∣S∣ = 8
- Probabilidade de cada resultado:
Cada sequência tem a mesma probabilidade: P(ai) = 1/8, para todo ai ∈ S
Evento A: Obter exatamente duas caras
As sequências com exatamente duas caras são: A={CCT, CTC, TCC}
Número de elementos favoráveis: |A| = 3.
Probabilidade:
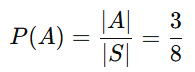
Evento B: Obter pelo menos uma cara
O evento B inclui todas as sequências exceto TTT:
B={CCC, CCT, CTC, CTT, TCC, TCT, TTC}
Número de elementos favoráveis: |B| = 7.
Probabilidade:
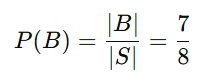
Importância dos Espaços Amostrais Equiprováveis
Os espaços amostrais equiprováveis são amplamente utilizados porque simplificam os cálculos e são aplicáveis em situações práticas como:
- Jogos de azar (dados, moedas, baralhos);
- Modelagem de experimentos científicos;
- Análise de situações simétricas no dia a dia.
Ao identificar que um experimento possui um espaço equiprovável, basta contar os elementos do evento e do espaço amostral para calcular probabilidades de forma eficiente.
Conclusão
Os espaços amostrais equiprováveis são fundamentais na teoria das probabilidades dentro da matemática, proporcionando uma base sólida para calcular probabilidades em situações simétricas. Seja no lançamento de moedas, em sorteios de cartas ou em lançamentos de dados, a ideia de equiprobabilidade simplifica os cálculos e facilita a análise. Com prática, esses conceitos podem ser aplicados com segurança em diferentes contextos do cotidiano e da ciência.













