As fórmulas da análise combinatória são ferramentas essenciais para resolver problemas que envolvem organização, seleção ou arranjo de elementos. Desde planejar atividades até criar estratégias em jogos, essas fórmulas ajudam a calcular possibilidades de forma eficiente e precisa.
Este artigo explica de maneira clara as principais fórmulas da análise combinatória, seus conceitos e exemplos práticos que mostram como aplicá-las no dia a dia.
📚 Quer aprofundar seus conhecimentos em Análise Combinatória e Probabilidade? Confira nossa recomendação dos melhores livros sobre o tema com exercícios resolvidos e dicas práticas. 👉Os melhores livros de Analise Combinatória e Probabilidade
As Principais Fórmulas da Análise Combinatória
Aqui está um resumo das principais fórmulas e suas aplicações.
| Conceito | Descrição | Fórmula |
|---|---|---|
| Princípio Fundamental da Contagem | Calcula o total de possibilidades multiplicando o número de opções de cada etapa. | n1×n2×n3… |
| Permutação Simples | Organiza todos os elementos de um conjunto distinto, onde a ordem importa. | P(n) = n! |
| Permutação com Repetição | Organiza elementos com repetições, ajustando para evitar contagens duplicadas. | 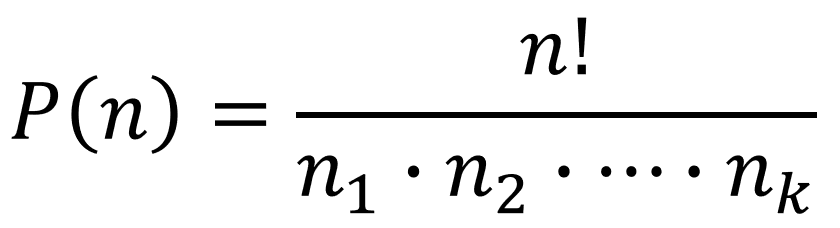 |
| Arranjo Simples | Seleciona e organiza parte dos elementos de um conjunto sem repetição, considerando a ordem. | 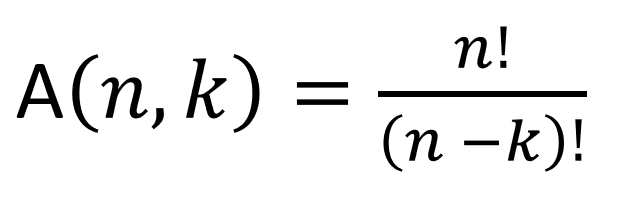 |
| Arranjo com Repetição | Seleciona e organiza parte dos elementos de um conjunto, permitindo repetição, considerando a ordem. | 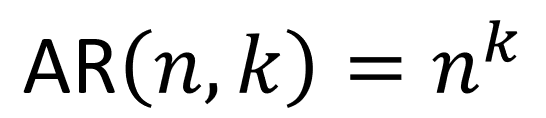 |
| Combinação Simples | Seleciona parte dos elementos de um conjunto, sem repetição e sem considerar a ordem. |  |
| Combinação com Repetição | Seleciona elementos de um conjunto permitindo repetição, sem considerar a ordem. |  |

Transforme seus estudos com o eBook Matemática Resumida: + de 90 Mapas Mentais de Matemática! Simplifique conceitos complexos, organize seus estudos e revise de forma prática e eficiente. Baixe agora e conquiste seus objetivos!
Exemplos Práticos das Fórmulas da Análise Combinatória
1. Princípio Fundamental da Contagem
Você tem 3 tipos de camisas e 2 tipos de calças. Quantos looks diferentes pode montar?
Cálculo: 3×2 = 6
2. Permutação Simples
Quantas formas diferentes existem para organizar 4 livros em uma prateleira?
Cálculo: P(4) = 4! = 4×3×2×1 = 24
👉Entre no nosso canal do WhatsApp
📘 Todas as fórmulas de matemática em um só lugar! Baixe agora nosso eBook gratuito
3. Permutação com Repetição
Quantas palavras diferentes podem ser formadas com as letras da palavra “MASSA”?
Cálculo:

4. Arranjo Simples
De 6 pessoas, quantas formas diferentes podemos escolher 2 para ocupar os cargos de presidente e vice-presidente (ordem importa)?
Cálculo:
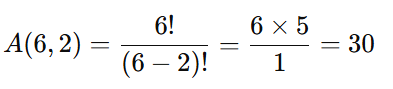
4.1. Arranjo com Repetição
Imagine que você deseja criar senhas de 3 caracteres usando as letras A, B e C, permitindo que as letras possam se repetir. Quantas senhas diferentes podem ser formadas?
Identificar os valores de n e k:
n: número total de elementos disponíveis (neste caso, n=3 letras: A, B, C).
k: número de elementos escolhidos para cada combinação (neste caso, k=3 caracteres por senha).
Aplicar a fórmula do arranjo com repetição:
A fórmula do arranjo com repetição é:
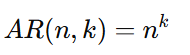
Substituir os valores na fórmula:
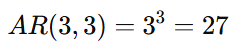
Resultado
Há 27 senhas diferentes que podem ser criadas.
5. Combinação Simples
De 5 amigos, quantos grupos de 3 podem ser formados para jogar futebol (ordem não importa)?
Cálculo:
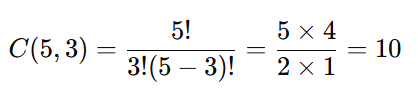
6. Combinação Composta
Quantas combinações de 3 bolas de sorvete podem ser feitas em uma sorveteria com 4 sabores, permitindo repetição?
Cálculo:
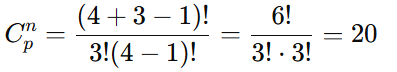
Quer dominar Análise Combinatória e Probabilidade de forma clara e aprofundada? Adquira já o livro Fundamentos de Matemática Elementar – Volume 5! Essa obra é referência para estudantes e concurseiros, trazendo teoria detalhada, exercícios resolvidos e aplicações práticas que vão turbinar seus estudos. Aproveite para garantir o seu e conquistar o sucesso nas provas!
Aplicações das Fórmulas da Análise Combinatória
As fórmulas da análise combinatória são amplamente aplicadas em diferentes áreas:
- Planejamento de Tarefas:
Organizar atividades em diferentes ordens. - Segurança Digital:
Criar senhas seguras usando arranjos e combinações. - Loterias e Jogos:
Calcular as chances de ganhar em jogos que envolvem seleção de números. - Pesquisa e Experimentos:
Selecionar amostras ou organizar condições de estudo. - Eventos e Cronogramas:
Planejar apresentações, mesas ou turnos.
Conclusão
As fórmulas da análise combinatória são indispensáveis para resolver problemas de contagem de maneira lógica e organizada. Seja em contextos acadêmicos, no trabalho ou no cotidiano, essas ferramentas simplificam questões complexas e ajudam a tomar decisões com base em cálculos precisos.
Com prática e compreensão, você pode aplicar essas fórmulas para resolver problemas de forma rápida e eficiente. Afinal, a matemática está presente em tudo, e a análise combinatória é uma das suas expressões mais úteis e práticas!













