A geometria espacial é uma área da matemática que estuda as propriedades e relações de figuras tridimensionais, como prismas, pirâmides, esferas, cones e cilindros. Para resolver problemas envolvendo essas formas, é essencial dominar as principais fórmulas de geometria espacial. Neste artigo, exploraremos em detalhes as geometria espacial fórmulas, abordando volume, área total, área lateral e outras propriedades dos sólidos geométricos. Além disso, usaremos variações do termo fórmulas geometria espacial para enriquecer seu entendimento, que está dentro todas das fórmulas matemática.
O Que É Geometria Espacial?
A geometria espacial estuda objetos tridimensionais que possuem comprimento, largura e altura. Essas figuras têm aplicações em diversas áreas, como engenharia, arquitetura e design. Diferente da geometria plana, que foca em figuras bidimensionais, a geometria espacial analisa o volume e a área das superfícies dos sólidos.
Algumas figuras comuns estudadas na geometria espacial incluem:
- Prismas;
- Pirâmides;
- Esferas;
- Cones;
- Cilindros;
- Paralelepípedos.
Confira também as fórmulas de geometria plana
Fórmulas de Geometria Espacial: Principais Conceitos
1. Fórmulas Cubo
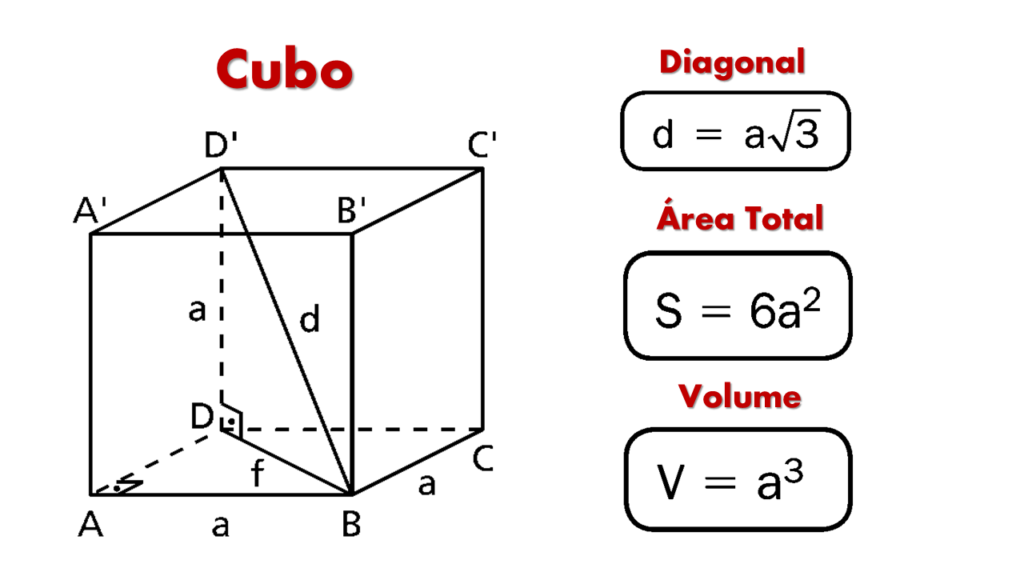
- Diagonal do Cubo:
d =a√3
- Área Total do Cubo:
V= 6a2
- Volume do Cubo:
V= a3
2. Fórmulas Paralelepípedo
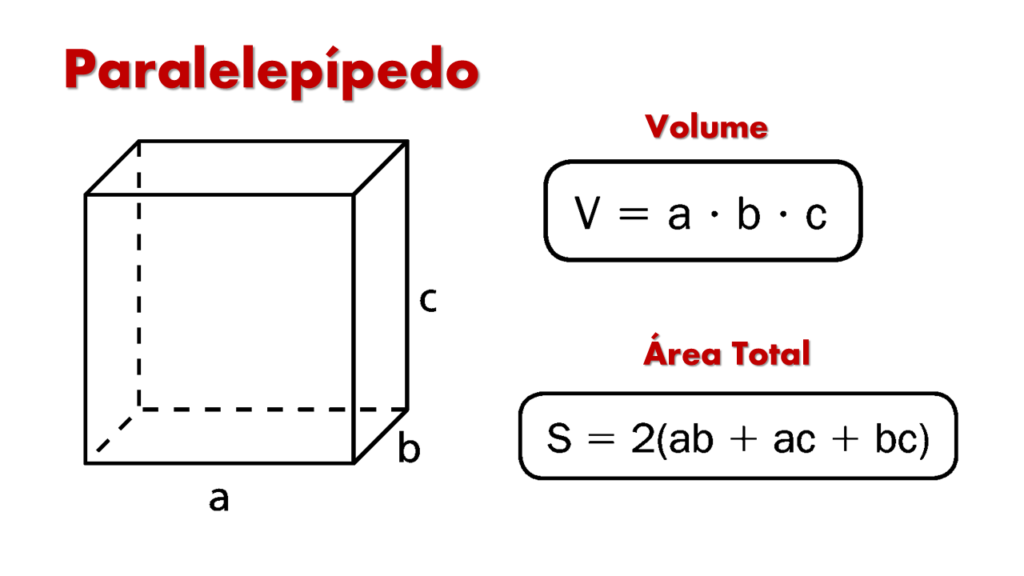
- Volume do Paralelepípedo:
V = a·b·c
- Área Lateral do Paralelepípedo:
S = 2(ab + ac + bc)
3. Fórmulas Prisma Regular
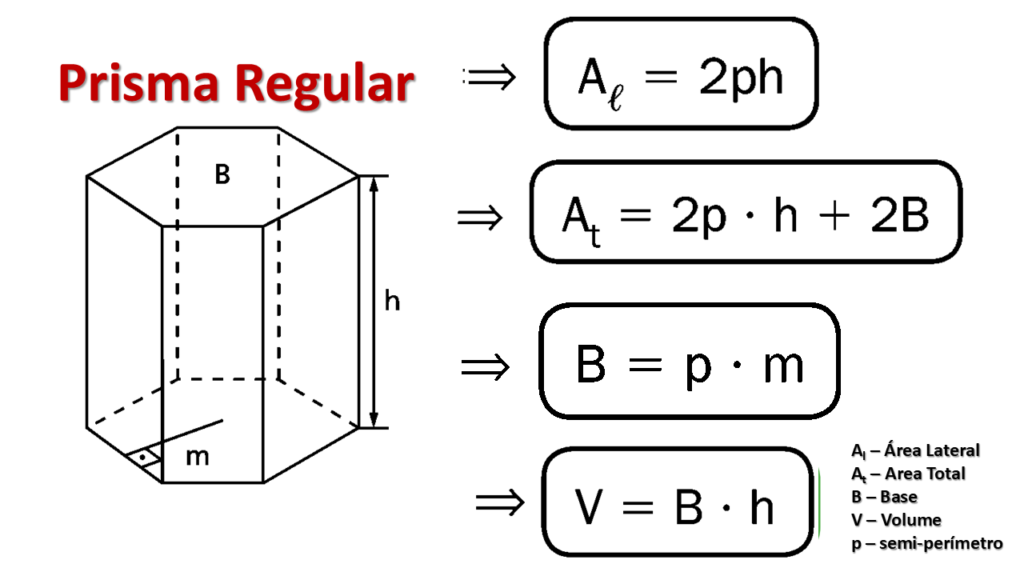
- Volume do Prisma Regular
V = B.h
- Área Lateral para o Prisma Regular
Al = 2ph
- Área Total para o Prisma Regular
At = 2ph + 2B
- Área da Base do Prisma Regular
B = pm
4. Fórmulas Pirâmide Regular
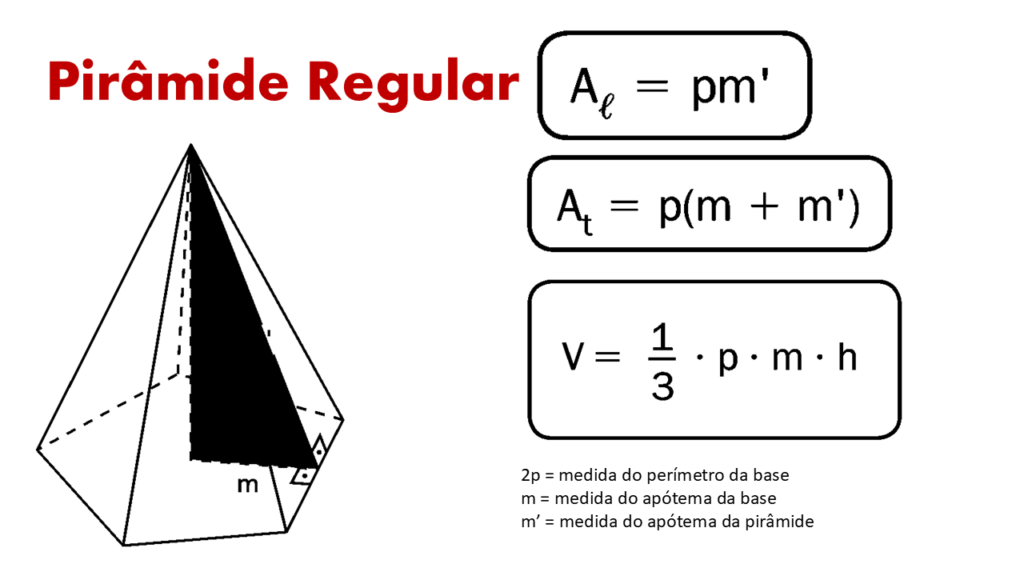
- Volume Pirâmide Regular:
V = 1/3·p·m·h
- Área Lateral Pirâmide Regular:
AL = pm´
- Área Total Pirâmide Regular:
AT = p(m + m´)
5. Fórmulas Cilindro Reto
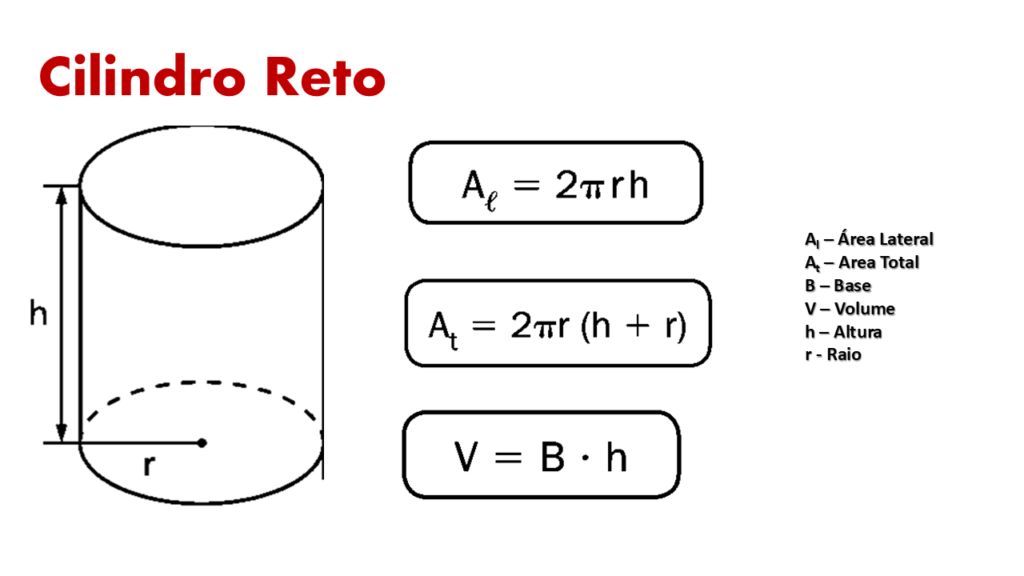
- Volume Cilindro Reto:
V = Bh = πr2h
- Área Lateral Cilindro Reto:
AL = 2πrh
- Área Total Cilindro Reto:
AT = 2πr(h + r)
6. Fórmulas Cone Reto
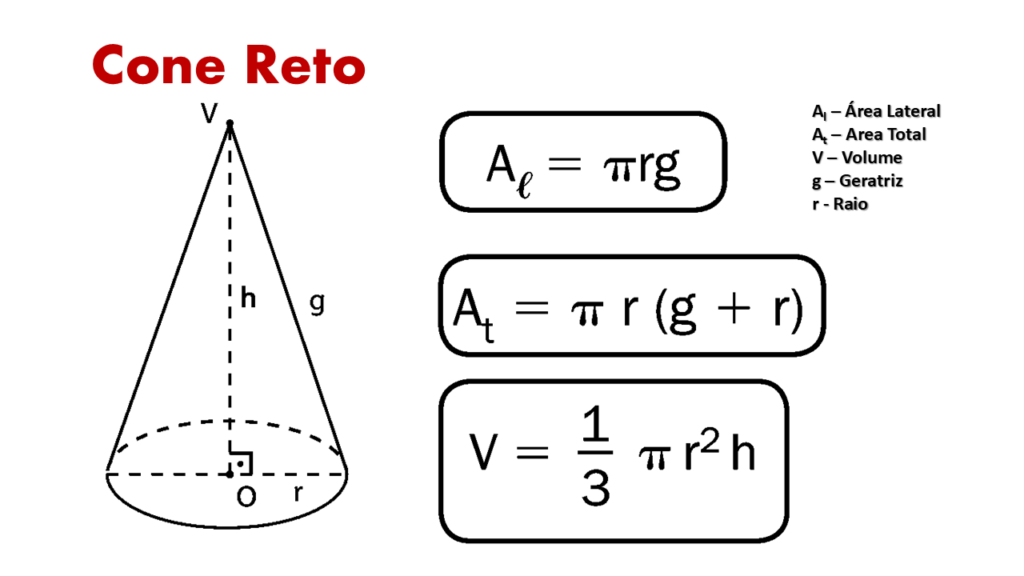
- Volume Cone Reto:
V =1/3 πr2h
- Área Lateral Cone Reto:
AL = πrg
- Área Total Cone Reto:
AT = πr(g + r)
7. Fórmulas Esfera

- Volume Esfera:
V =4/3 πr3
- Volume Cunha Esfera:
V = (πr3α)/270
- Área Esfera:
A = 4πr2
- Área Esfera:
A = (πr2α)/90
Teorema de Euler para Poliedros
O teorema de Euler estabelece uma relação entre o número de vértices (V), arestas (A) e faces (F) de um poliedro convexo:
V − A + F = 2V – A + F = 2
Exemplo: Em um cubo:
- V = 8, A = 12, F = 6.
- Verificação: 8 – 12 + 6 = 2.
Confira também a fórmula de permutação
Confira também as fórmulas de geometria plana
Dicas para Estudar Geometria Espacial
- Visualize os Sólidos: Use modelos 3D ou desenhos para compreender melhor as formas.
- Organize as Fórmulas: Crie resumos com as fórmulas mais usadas.
- Resolva Exercícios: A prática é fundamental para fixar os conceitos.
Entre para o nosso Canal do WhatsApp
Conclusão
As fórmulas de geometria espacial são indispensáveis para o cálculo de volumes, áreas e outras propriedades de sólidos tridimensionais. Com este guia, você tem à disposição as principais geometria espacial fórmulas, organizadas de forma clara e objetiva. Continue praticando e explorando o mundo fascinante da geometria espacial para resolver problemas com precisão e eficiência!














