Introdução
A trigonometria é uma das áreas mais antigas da matemática, essencial para a compreensão das relações entre os lados e ângulos de triângulos. Ela também desempenha um papel crucial na modelagem de fenômenos periódicos, como ondas sonoras e luz. Neste artigo, exploraremos as principais fórmulas trigonométricas, que são fundamentais para resolver problemas em diversas áreas, desde a engenharia até a física e a computação gráfica.
Funções Trigonométricas Básicas
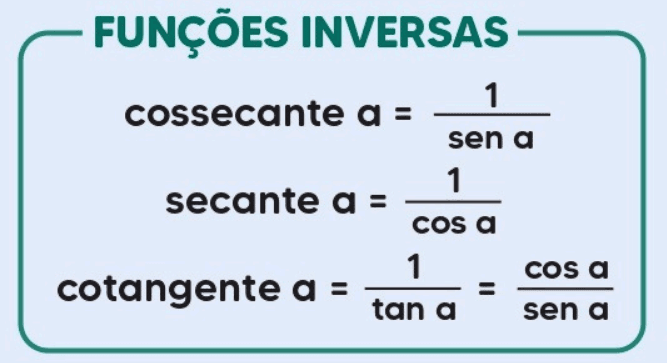
As funções trigonométricas básicas são o seno (sin), o cosseno (cos) e a tangente (tan). Estas funções estão relacionadas aos ângulos de um triângulo retângulo e são definidas como:
- Seno (sin): É a razão entre o cateto oposto ao ângulo e a hipotenusa.

- Cosseno (cos): É a razão entre o cateto adjacente ao ângulo e a hipotenusa.
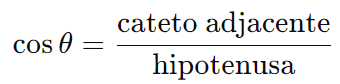
- Tangente (tan): É a razão entre o cateto oposto e o cateto adjacente.
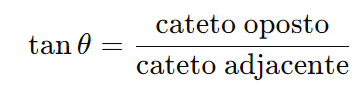
Identidades Trigonométricas Fundamentais
As identidades trigonométricas são equações que envolvem funções trigonométricas e são verdadeiras para todos os valores dos ângulos envolvidos. As principais identidades são:
1. Identidade de Pitágoras
Esta identidade expressa a relação fundamental entre seno e cosseno:
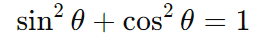
Dividindo por cos2θ ou sin2θ , obtêm-se outras duas identidades:
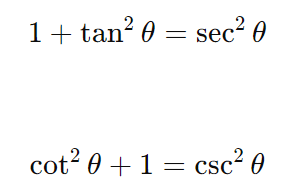
2. Fórmulas de Adição e Subtração de Ângulos
Estas fórmulas permitem calcular o seno, cosseno e tangente da soma ou diferença de dois ângulos.
- Seno da soma e diferença:
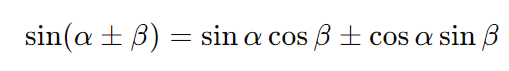
- Cosseno da soma e diferença:
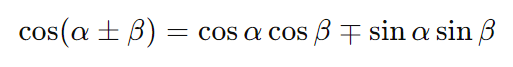
- Tangente da soma e diferença:
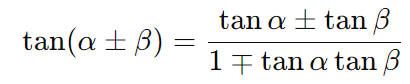
3. Fórmulas de Duplo e Meio Ângulo
Estas fórmulas são usadas para expressar as funções trigonométricas de um ângulo duplo ou metade de um ângulo.
- Seno do ângulo duplo:
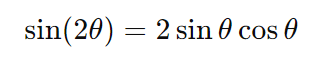
- Cosseno do ângulo duplo:

ou

ou
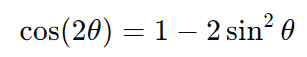
- Tangente do ângulo duplo:
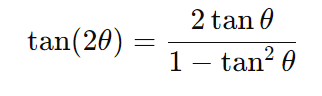
- Seno do meio ângulo:
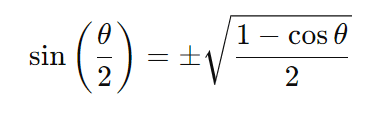
- Cosseno do meio ângulo:
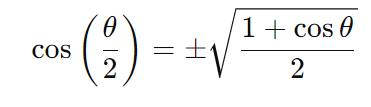
- Tangente do meio ângulo:
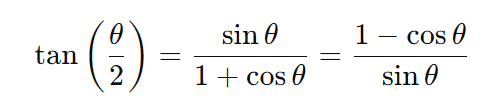
4. Fórmulas de Produto a Soma
Estas fórmulas são usadas para converter produtos de funções trigonométricas em somas ou diferenças.
- Produto de senos:
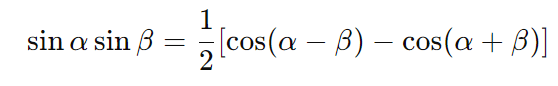
- Produto de cossenos:
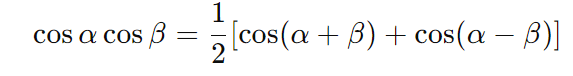
- Produto de seno e cosseno:
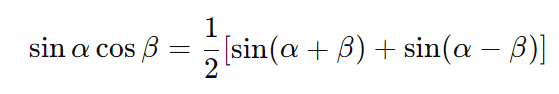
5. Fórmulas de Soma a Produto
Estas fórmulas permitem converter somas de funções trigonométricas em produtos.
- Soma de senos:
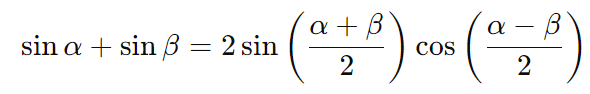
- Diferença de senos:
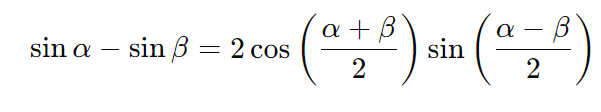
- Soma de cossenos:
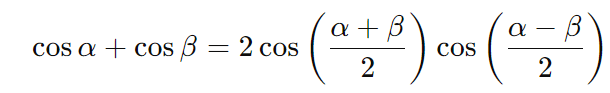
- Diferença de cossenos:
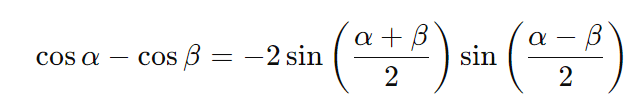
Aplicações das Fórmulas Trigonométricas
As fórmulas trigonométricas são amplamente utilizadas em várias disciplinas. Na física, elas ajudam a modelar ondas e oscilações, enquanto na engenharia são essenciais para o projeto de estruturas e a análise de forças. Na computação gráfica, as transformações trigonométricas são usadas para criar animações e simulações realistas. Além disso, na astronomia, essas fórmulas são fundamentais para calcular distâncias e ângulos entre corpos celestes.
Conclusão
As fórmulas trigonométricas são ferramentas poderosas que permitem a resolução de uma vasta gama de problemas em matemática e ciências aplicadas. Desde as identidades básicas até as mais complexas transformações de ângulos, o domínio dessas fórmulas é essencial para qualquer estudante ou profissional que lide com matemática. Ao compreender e aplicar essas fórmulas, podemos explorar com maior profundidade os padrões e fenômenos que governam o mundo ao nosso redor.