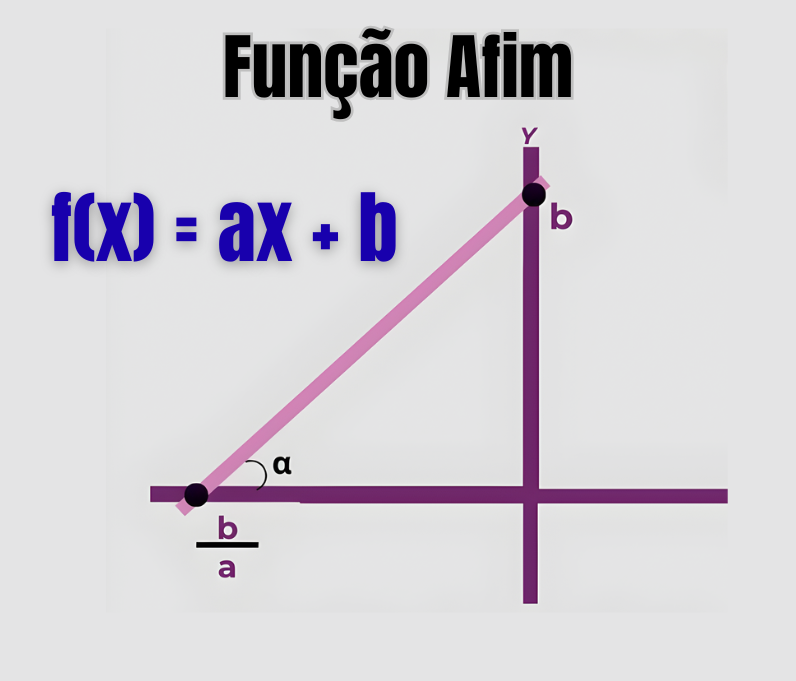
Para compreender o que é função do primeiro grau, deve-se saber que é aquela escrita na forma y = ax + b ou f(x) = ax + b, em que a e b são reais e a é diferente de zero.
O que é uma função?
Uma função é uma expressão matemática que estabelece uma correspondência entre cada elemento x de um conjunto A e um único elemento y de um conjunto B. Os conjuntos A e B são chamados de domínio e contradomínio, respectivamente. As variáveis x e y são conhecidas como variável independente e variável dependente, respectivamente, pois o valor de y depende do valor de x.
Funções do primeiro grau são aquelas em que a variável independente aparece elevada à potência 1. O grau de uma função é determinado pelo maior expoente da variável independente e, no caso das funções do primeiro grau, esse expoente máximo é 1.
“Mapa Mental: Gráfico de função do 1º Grau”
Exemplos de função do primeiro grau
Os exemplos a seguir são de funções do primeiro grau. Isso significa que elas podem ser escritas na forma y = ax + b, ou já estão nessa forma.
a) y = -4x + 10. Essa é uma função afim, ou do primeiro grau, em que a = -4 e b = 10.
b) y = x – 6. Embora o sinal de – 6 não seja positivo, essa também é uma função do primeiro grau, com a = 1 e b = – 6. Para que não haja dúvidas, basta escrevê-la: y = (1)x + (–6).
Exemplo
Construa o gráfico da função f(x) = 2x + 3.
Solução
Para construir o gráfico desta função, vamos atribuir valores arbitrários para x, substituir na equação e calcular o valor correspondente para a f (x).
Sendo assim, iremos calcular a função para os valores de x iguais a: – 2, – 1, 0, 1 e 2. Substituindo esses valores na função, temos:
f (- 2) = 2. (- 2) + 3 = – 4 + 3 = – 1
f (- 1) = 2 . (- 1) + 3 = – 2 + 3 = 1
f (0) = 2 . 0 + 3 = 3
f (1) = 2 . 1 + 3 = 5
f (2) = 2 . 2 + 3 = 7
Os pontos escolhidos e o gráfico da f (x) são apresentados na imagem abaixo:
No exemplo, utilizamos vários pontos para construir o gráfico, entretanto, para definir uma reta bastam dois pontos.
Para facilitar os cálculos podemos, por exemplo, escolher os pontos (0,y) e (x,0). Nestes pontos, a reta da função corta o eixo Ox e Oy respectivamente.
Funções Crescentes e Decrescentes
Uma função é considerada crescente quando, ao atribuirmos valores progressivamente maiores para x, o valor de f(x) também aumenta.
Por outro lado, uma função é decrescente quando, ao atribuir valores maiores para x, o valor de f(x) diminui.
Para determinar se uma função do primeiro grau é crescente ou decrescente, basta observar o valor do coeficiente angular.
Se o coeficiente angular for positivo, ou seja, se a for maior que zero, a função será crescente. Caso contrário, se a for negativo, a função será decrescente.
Por exemplo, a função 2x – 4 é crescente, pois a = 2 (um valor positivo). Já a função -2x – 4 é decrescente, pois a = -2 (um valor negativo). Essas funções estão ilustradas nos gráficos abaixo:
Na definição também foi dito que sob certas condições, uma função f : ℝ → ℝ é uma função afim. Essa expressão parece complicada, mas na verdade ela só está querendo nos mostrar que o domínio ou conjunto de partida, e que o contradomínio ou conjunto de chegada da função afim, é conjunto dos números reais. Isso significa que números positivos, negativos, frações, dízimas periódicas, raízes não exatas e todo e qualquer número real pode fazer parte do domínio e do contradomínio desta função, sem que haja qualquer restrição.
Agora vamos analisar mais um detalhe extremamente interessante. A fórmula da função afim “f (x) = ax + b” é composta por uma soma de 2 termos: ax e b. Um termo carrega consigo a variável x, mas o outro não possui qualquer variável. a e b são números reais chamados de coeficientes, e enquanto a é dependente da variável x, b não possui qualquer relação com ela. É por isso que conhecemos b como termo independente da função afim.
Exercícios
1 – Dada a função f ( x ) = 3x – 7 determine:
A) f ( x ) = 0
B) f ( x ) = 1
C) f ( x ) = −2
2 – Considere a função g( x ) = − 4x + 8 e calcule:
A) g( x ) = 8
B) g( x ) = 6
C) g( x ) = −3
3 – Determine os zeros ou raízes das funções:
A) f ( x ) = − 4x – 8
B) g( x ) = 2x + 20
C) h( x ) = 8x + 10
4 – Faça um esboço do gráfico da função:
A) f ( x ) = − 2x + 8
B) g( x ) = − 3x + 6
C) h( x ) = − 4x − 4
D) i( x ) = − 5x + 3
5 – Determine a lei da função afim cujo gráfico passa pelos pontos:
A) (0 ,1) e (0 ,1)
B) (0 ,1) e (-1 ,0)
C) (2, 0) e (0 ,-2 )
D) (1, -1) e (3 ,3)
E) (2 , 1) e (5 ,10)
F) (-3 ,0) e (12 ,21)
6 – Considere o gráfico abaixo e assinale a alternativa onde aparece a função que o representa.
7 –
Durante o mês de dezembro, uma loja de cosméticos obteve um total de R$ 900,00 pelas vendas de um certo perfume. Com a chegada do mês de janeiro, a loja decidiu dar um desconto para estimular as vendas, baixando o preço desse perfume em R$ 10,00. Com isso, vendeu em janeiro 5 perfumes a mais do que em dezembro, obtendo um total de R$ 1.000,00 pelas vendas de janeiro. O preço pelo qual esse perfume foi vendido em dezembro era de:
A) R$ 55,00. D) R$ 70,00.
B) R$ 60,00. E) R$ 75,00.
C) R$ 65,00.
Problemas de Funções do Primeiro Grau ou Afim Aplicados ao Cotidiano
1. Plano de Academia
Uma academia cobra R$ 150 por mês e uma taxa de inscrição de R$ 100. Qual das funções abaixo descreve o custo total f(x) após x meses de assinatura?
a) f(x) = 150x + 100
b) f(x) = 150x
c) f(x) = 100x + 150
d) f(x) = 100x
Solução:
A função correta é a a) f(x) = 150x + 100. A taxa de inscrição de R$ 100 é um valor fixo pago apenas uma vez, e os R$ 150 são multiplicados pelo número de meses x.
2. Assinatura de Revista
Uma assinatura de revista custa R$ 20 por mês, mais uma taxa de envio única de R$ 30. Quais das funções abaixo descrevem o custo total f(x) após x meses de assinatura?
a) f(x) = 20x + 30
b) f(x) = 20x
c) f(x) = 30x + 20
d) f(x) = 30x
Solução:
A função correta é a a) f(x) = 20x + 30. O custo total é composto pela taxa de envio fixa de R$ 30 e pelo custo mensal de R$ 20 multiplicado pelo número de meses x.
3. Plano de Telefonia
Um plano de telefonia custa R$ 50 por mês, mais uma taxa de ativação de R$ 40. Quais das funções abaixo descrevem o custo total f(x) após x meses?
a) f(x) = 50x + 40
b) f(x) = 40x + 50
c) f(x) = 50x
d) f(x) = 90x
Solução:
A função correta é a a) f(x) = 50x + 40. A taxa de ativação de R$ 40 é um valor fixo, enquanto os R$ 50 são multiplicados pelo número de meses x.
4. Empréstimo
Uma pessoa pega um empréstimo que requer um pagamento fixo de R$ 300 por mês, mais uma taxa inicial de administração de R$ 500. Quais das funções abaixo descrevem o valor total f(x) pago após x meses?
a) f(x) = 300x + 500
b) f(x) = 500x + 300
c) f(x) = 300x
d) f(x) = 500x
Solução:
A função correta é a a) f(x) = 300x + 500. A taxa de administração de R$ 500 é um valor fixo, e o pagamento mensal de R$ 300 é multiplicado pelo número de meses x.
5. Serviço de Streaming
Um serviço de streaming custa R$ 25 por mês, com uma taxa de ativação única de R$ 15. Quais das funções abaixo descrevem o custo total f(x) após x meses?
a) f(x) = 25x + 15
b) f(x) = 15x + 25
c) f(x) = 25x
d) f(x) = 40x
Solução:
A função correta é a a) f(x) = 25x + 15. O valor de R$ 15 é uma taxa fixa, enquanto os R$ 25 são multiplicados pelo número de meses x.
6. Curso Online
Um curso online cobra R$ 200 por mês, mais uma taxa de matrícula de R$ 150. Quais das funções abaixo descrevem o custo total f(x) após x meses de curso?
a) f(x) = 200x + 150
b) f(x) = 150x + 200
c) f(x) = 200x
d) f(x) = 150x
Solução:
A função correta é a a) f(x) = 200x + 150. A taxa de matrícula de R$ 150 é um valor fixo, e os R$ 200 são multiplicados pelo número de meses x.
7. Plano de Saúde
Um plano de saúde custa R$ 400 por mês, mais uma taxa de adesão de R$ 250. Quais das funções abaixo descrevem o custo total f(x) após x meses?
a) f(x) = 400x + 250
b) f(x) = 250x + 400
c) f(x) = 400x
d) f(x) = 250x
Solução:
A função correta é a a) f(x) = 400x + 250. A taxa de adesão de R$ 250 é um valor fixo, enquanto os R$ 400 são multiplicados pelo número de meses x.
8. Plano de Academia
Uma academia cobra R$ 150 por mês e uma taxa de inscrição de R$ 100. Após 6 meses de assinatura, quanto terá sido pago no total?
a) R$ 900
b) R$ 1000
c) R$ 1100
d) R$ 1000
Solução:
A função é f(x) = 150x + 100. Após 6 meses (x = 6):
f(6) = 150(6) + 100 = 900 + 100 = R$ 1000
Resposta correta: d) R$ 1000
9. Assinatura de Revista
Uma assinatura de revista custa R$ 20 por mês, mais uma taxa de envio única de R$ 30. Qual será o custo total após 12 meses?
a) R$ 240
b) R$ 270
c) R$ 250
d) R$ 280
Solução:
A função é f(x) = 20x + 30. Após 12 meses (x = 12):
f(12) = 20(12) + 30 = 240 + 30 = R$ 270
Resposta correta: b) R$ 270
10. Plano de Telefonia
Um plano de telefonia custa R$ 50 por mês, mais uma taxa de ativação de R$ 40. Qual será o custo total após 10 meses?
a) R$ 490
b) R$ 540
c) R$ 580
d) R$ 600
Solução:
A função é f(x) = 50x + 40. Após 10 meses (x = 10):
f(10) = 50(10) + 40 = 500 + 40 = R$ 540
Resposta correta: b) R$ 540
11. Empréstimo
Uma pessoa pega um empréstimo que requer um pagamento fixo de R$ 300 por mês, mais uma taxa inicial de administração de R$ 500. Quanto terá sido pago após 8 meses?
a) R$ 2400
b) R$ 2900
c) R$ 3400
d) R$ 3800
Solução:
A função é f(x) = 300x + 500. Após 8 meses (x = 8):
f(8) = 300(8) + 500 = 2400 + 500 = R$ 2900
Resposta correta: b) R$ 2900
12. Serviço de Streaming
Um serviço de streaming custa R$ 25 por mês, com uma taxa de ativação única de R$ 15. Quanto terá sido pago após 15 meses?
a) R$ 375
b) R$ 365
c) R$ 390
d) R$ 400
Solução:
A função é f(x) = 25x + 15. Após 15 meses (x = 15):
f(15) = 25(15) + 15 = 375 + 15 = R$ 390
Resposta correta: c) R$ 390
13. Curso Online
Um curso online cobra R$ 200 por mês, mais uma taxa de matrícula de R$ 150. Qual será o custo total após 5 meses de curso?
a) R$ 950
b) R$ 1050
c) R$ 1150
d) R$ 1250
Solução:
A função é f(x) = 200x + 150. Após 5 meses (x = 5):
f(5) = 200(5) + 150 = 1000 + 150 = R$ 1150
Resposta correta: c) R$ 1150
14. Plano de Saúde
Um plano de saúde custa R$ 400 por mês, mais uma taxa de adesão de R$ 250. Quanto será pago ao final de 12 meses?
a) R$ 4800
b) R$ 4850
c) R$ 4900
d) R$ 5050
Solução:
A função é f(x) = 400x + 250. Após 12 meses (x = 12):
f(12) = 400(12) + 250 = 4800 + 250 = R$ 5050
Resposta correta: d) R$ 5050
Aplicações das Funções do Primeiro Grau
Funções do primeiro grau, também conhecidas como funções lineares, possuem diversas aplicações práticas em diferentes áreas do conhecimento. Essas funções, que têm a forma geral f(x)= ax + b, onde a e b são constantes, são amplamente utilizadas para modelar situações onde há uma relação linear entre duas variáveis.
1. Economia e Finanças
No campo da economia, as funções do primeiro grau são utilizadas para descrever a relação entre o custo total de produção e a quantidade de bens produzidos. Por exemplo, o custo total C(x) de produzir x unidades de um produto pode ser modelado por uma função linear onde a representa o custo variável por unidade e b o custo fixo. Essa função permite prever os custos e, consequentemente, determinar os preços para obter lucro.
2. Física
Na física, as funções lineares aparecem em diversas situações, como na descrição de movimentos uniformes, onde a distância percorrida por um objeto em movimento uniforme é proporcional ao tempo. Nesse caso, a equação s(t)=vt+s0, onde v é a velocidade constante e s0 é a posição inicial, é uma função do primeiro grau que relaciona a posição s com o tempo t.
3. Engenharia
Na engenharia, as funções do primeiro grau são usadas para projetar sistemas e processos que envolvem variáveis que se relacionam de forma linear. Por exemplo, na engenharia elétrica, a resistência total em um circuito em série pode ser descrita por uma função linear da resistência individual de cada componente.
4. Ciências Sociais
Em sociologia e outras ciências sociais, funções lineares são utilizadas para analisar tendências em dados coletados. Por exemplo, a relação entre o número de horas de estudo e o desempenho acadêmico de um aluno pode ser modelada linearmente, ajudando a prever resultados e a orientar estratégias educacionais.
5. Negócios e Marketing
No contexto empresarial, as funções do primeiro grau são úteis para determinar a relação entre investimento em marketing e vendas. Uma função linear pode descrever como um aumento no investimento em publicidade afeta as vendas, ajudando as empresas a otimizar seus gastos e maximizar o retorno sobre o investimento.
6. Agronomia
Na agronomia, as funções lineares podem ser usadas para relacionar a quantidade de insumos, como fertilizantes ou água, com o rendimento das colheitas. Isso permite aos agricultores tomar decisões mais informadas sobre como alocar recursos para maximizar a produção.
Essas são apenas algumas das muitas aplicações das funções do primeiro grau. A simplicidade e a versatilidade desse tipo de função fazem dela uma ferramenta essencial em diversas áreas, permitindo a modelagem e a análise de uma ampla gama de problemas do mundo real.
