Introdução
A função do primeiro grau é um conceito fundamental em matemática, amplamente utilizado em diversas áreas do conhecimento e situações do cotidiano. Também conhecida como função linear, a função do primeiro grau é representada por uma equação na forma f(x)=ax + b. Esse tipo de função descreve uma relação direta e linear entre duas variáveis, onde uma depende da outra de forma proporcional.
Equação para Determinar o Valor da Variável Independente (x)
A função do primeiro grau, também conhecida como função afim, é um conceito matemático que estabelece uma relação direta entre duas variáveis em uma equação, mostrando como uma variável depende da outra. Em uma função do primeiro grau, a variável dependente, normalmente representada por y, depende diretamente da variável independente x. Essa relação é descrita pela equação:
y= ax + b ou f(x) = ax + b
Nessa equação:
- a e b são números reais, onde a ≠ 0.
- a é o coeficiente angular, responsável pela inclinação da reta no gráfico.
- b é o coeficiente linear, que indica o ponto em que a reta intercepta o eixo y.
A função é chamada de “primeiro grau” porque a maior potência da variável x é igual a 1 (ou x1). O grau de uma função é determinado pelo maior expoente da variável independente. Portanto, se o expoente for 1, a função é de primeiro grau; se for 2, a função é de segundo grau, e assim por diante.
Para dominar a Função Afim, precisa aprender as equações do primeiro grua
Domínio e Imagem
O conjunto de valores que a variável x pode assumir é chamado de domínio, enquanto os valores correspondentes de y, resultantes da aplicação da função, formam a imagem ou contradomínio. As variáveis x e y são chamadas de variável independente e variável dependente, respectivamente, porque y depende dos valores de x.
Exemplo de Função de Primeiro Grau
A função do primeiro grau pode ser expressa como:
y= ax + b
Aqui estão alguns exemplos:
- y = 5x+7 (onde a=5 e b=7)
- y=−4x + 20 (onde a=−4 e b=20)
- y=8x (onde a=8 e b=0)
Note que mesmo quando o coeficiente a é negativo, como no segundo exemplo, a função ainda é do primeiro grau. Se o termo b não estiver presente na equação, ele é considerado zero, como no terceiro exemplo.
Resolução de Funções do Primeiro Grau
O objetivo principal ao trabalhar com funções do primeiro grau é determinar o valor da variável desconhecida xxx, conhecida como incógnita. As letras x, y e z são comumente usadas para representar essas variáveis. Veja um exemplo de como resolver uma função do primeiro grau:
y = ax + b
Suponha que: 20=3x + 5
Para encontrar o valor de x, siga os passos:
- Subtraia 5 de ambos os lados da equação:
20−5=3×20 – 5 = 3×20−5=3x
- Isso resulta em:
15 = 3x
- Em seguida, divida ambos os lados por 3 para isolar x:
x=15/3=5
Aqui, aplicamos o princípio de que, ao mover um termo de um lado da equação para o outro, sua operação deve ser invertida (adição torna-se subtração, multiplicação torna-se divisão, etc.).
Tratamento de Equações com Variável Negativa
Quando a variável x possui um coeficiente negativo, multiplica-se todos os termos da equação por -1 para simplificar a resolução. Considere o exemplo: 12=−2x + 10
Multiplicando todos os termos por -1: −12 = 2x−10
Agora, resolva como uma equação padrão:
−12 + 10 = 2x
−2=2x
x=−2/2=−1
Definição e Propriedades
Uma função do primeiro grau é dada pela expressão: f(x) = ax + b
Onde:
- x é a variável independente (domínio da função).
- a é o coeficiente angular, que determina a inclinação da reta no gráfico.
- b é o coeficiente linear, que indica onde a reta intercepta o eixo y.
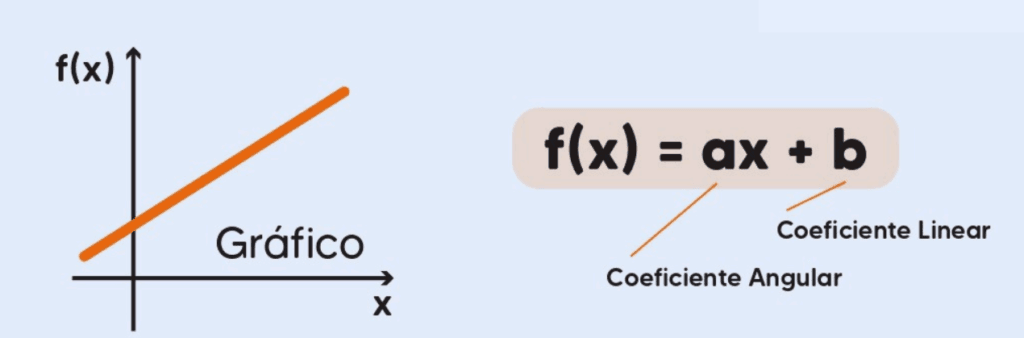
Características Principais:
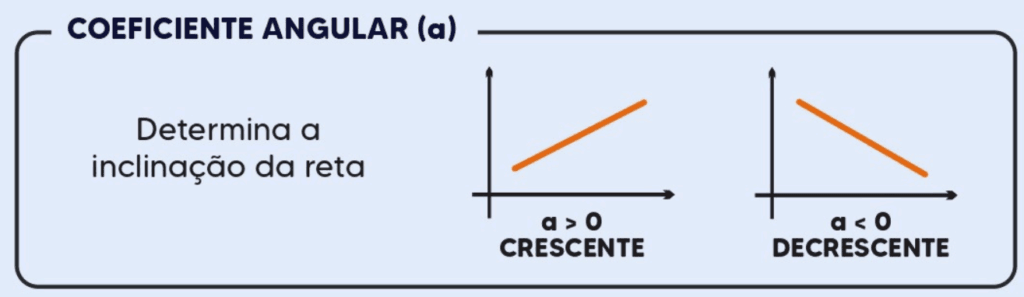
- Gráfico: O gráfico de uma função do primeiro grau é sempre uma linha reta. A inclinação dessa linha é determinada pelo valor de a:
- Se a > 0, a reta é crescente, indicando que a função aumenta à medida que x cresce.
- Se a<0, a reta é decrescente, mostrando que a função diminui à medida que x aumenta.
- Se a=0, a reta é horizontal, o que significa que o valor de y permanece constante, independentemente de x.
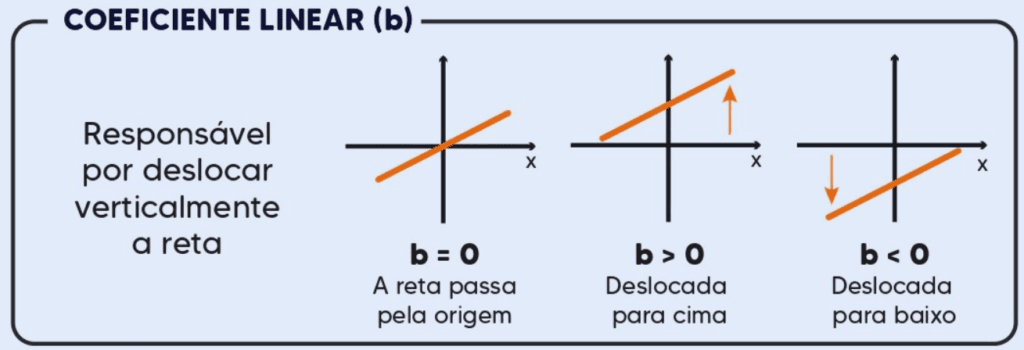
- Raiz da Função: A raiz, ou zero da função, é o valor de x para o qual f(x)=0 (valor de x onde o y é zero). Para encontrar a raiz, resolvemos a equação ax + b=0, resultando em x = −b/a. Esse é o ponto onde a reta cruza o eixo x no gráfico.
Exemplo 1: Raiz da Função em um Empréstimo
Suponha que você tenha feito um empréstimo onde a dívida total diminui de forma linear com os pagamentos mensais. A função que descreve o valor restante da dívida D(x) em função do número de meses ( x ) é dada por:
D(x) = 1000 – 200x
Neste caso:
- O valor inicial da dívida é R$ 1.000,00 (representado por b = 1000).
- O valor que você paga mensalmente é de R$ 200,00 (representado por a = -200).
A raiz da função é o ponto em que a dívida se torna zero, ou seja, D(x) = 0:
1000 – 200x = 0
Resolvendo a equação para ( x ):
200x = 1000
x = 1000/200 = 5
Interpretação: A raiz da função ocorre quando ( x = 5 ), ou seja, após 5 meses de pagamento, a dívida será totalmente quitada.
Exemplo 2: Raiz da Função em um Lucro de Venda
Imagine que você está vendendo ingressos para um show, e há um custo fixo de R$ 500,00 para organizar o evento. Cada ingresso é vendido por R$ 25,00. A função que descreve o lucro L(x) em função do número de ingressos vendidos x é:
L(x) = 25x – 500
Neste caso:
- ( a = 25 ) representa o lucro por ingresso.
- ( b = -500 ) é o custo fixo inicial.
Para encontrar a raiz da função, ou seja, o ponto em que o lucro é zero (o ponto de equilíbrio), resolvemos L(x) = 0:
25x – 500 = 0
25x = 500
x = 500/25 = 20
Interpretação: A raiz da função ocorre quando ( x = 20 ). Isso significa que você precisa vender exatamente 20 ingressos para cobrir os custos e começar a ter lucro.
Construção de um Gráfico
Exemplo 1: Vamos construir o gráfico da função y = 2x − 1 ou f(x)= 2x − 1 , onde a = 2 e b=−1.
Para construir o gráfico, escolha alguns valores de x e calcule os correspondentes valores de y:
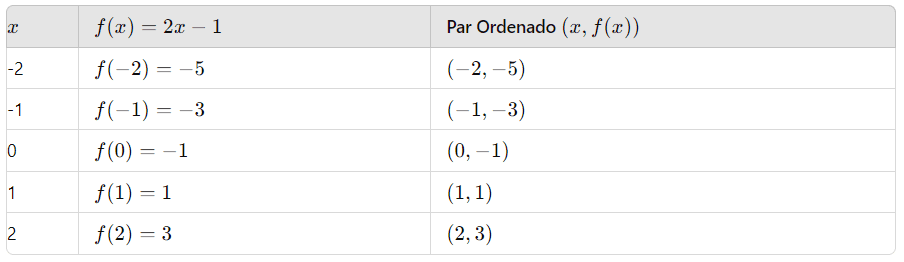
Construindo o gráfico temos:
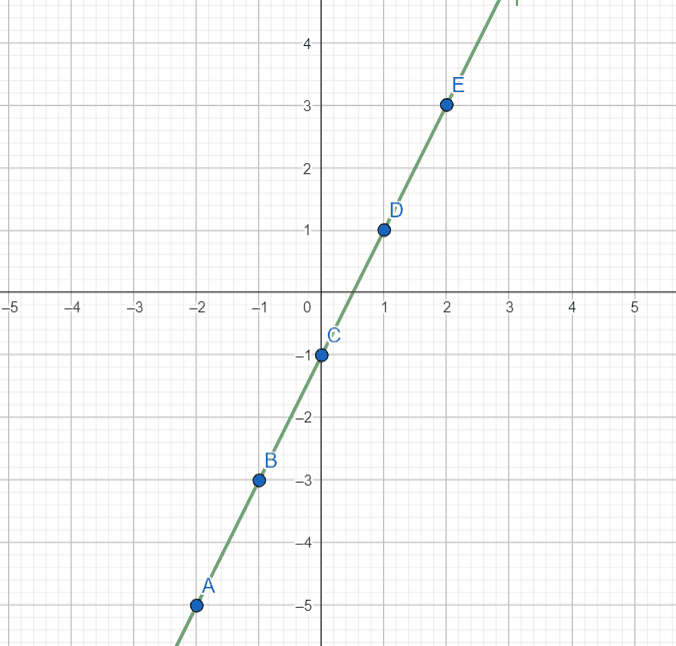
Exemplo 2: Vamos construir o gráfico da função f(x) = -2x + 4
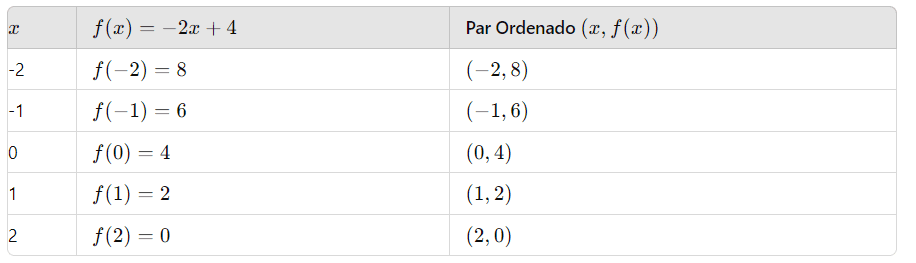
Marcando os pontos no plano cartesiano temos:
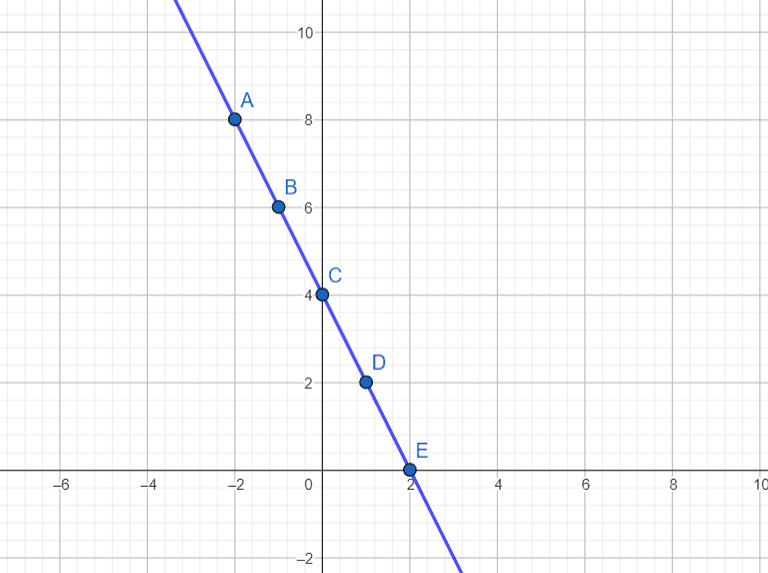
Função Crescente e Decrescente
Uma função é considerada crescente quando, ao atribuir valores sucessivamente maiores à variável x, o resultado da função f(x) também aumenta. Em outras palavras, conforme x cresce, f(x) também cresce.
Por outro lado, uma função é decrescente quando, ao atribuir valores maiores a x, o valor de f(x) diminui. Nesse caso, conforme x aumenta, o valor de f(x) se torna menor.
Para determinar se uma função afim é crescente ou decrescente, é necessário examinar o valor do coeficiente angular ( a ) da função.
- Se o coeficiente angular ( a ) for positivo (ou seja, ( a > 0 )), a função será crescente.
- Se o coeficiente angular ( a ) for negativo (ou seja, ( a < 0 )), a função será decrescente.
Por exemplo, a função f(x) = 2x – 4 é crescente, pois o coeficiente angular ( a = 2 ) é positivo. Em contrapartida, a função f(x) = -2x – 4 é decrescente, já que ( a = -2 ) é negativo. Essas características podem ser visualizadas nos gráficos correspondentes.
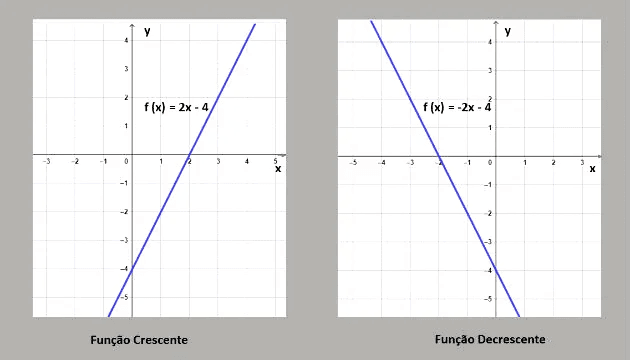
Aplicações Cotidianas da Função do Primeiro Grau
As funções do primeiro grau têm uma vasta gama de aplicações práticas, pois muitas relações do mundo real podem ser modeladas por elas. A seguir, veremos alguns exemplos que demonstram como esse conceito é aplicado em diferentes contextos.
Exemplo 1: Cálculo do Custo de uma Corrida de Táxi
Imagine que você precisa calcular o custo de uma corrida de táxi. Suponha que o preço da corrida seja composto por uma tarifa fixa de R$ 5,00, mais R$ 2,00 por quilômetro rodado. A função que descreve o custo total C(x), em função da distância percorrida x, pode ser escrita como:
C(x)= 2x + 5
Neste caso, o coeficiente angular a=2 representa o custo por quilômetro, e o coeficiente linear b=5 é a tarifa fixa. Se a corrida foi de 10 km, o custo total será:
C(10) = 2(10) + 5 = 20 + 5 = R$ 25,00
Essa função do primeiro grau facilita a previsão do custo da corrida com base na distância percorrida.
Exemplo 2: Raiz da Função no Ponto de Equilíbrio de um Evento
Imagine que você está organizando um evento e precisa vender ingressos para cobrir os custos. O custo fixo para realizar o evento é de R$ 500,00. Cada ingresso é vendido por R$ 25,00. A função que descreve o lucro L(x) em função do número de ingressos vendidos x é: L(x)=25x − 500
Neste caso:
- a=25 representa o lucro por ingresso vendido.
- b=−500 é o custo fixo inicial.
Para encontrar a raiz da função, ou seja, o ponto em que o lucro é zero (o ponto de equilíbrio), resolvemos L(x)=0,
L(x)=0:
25x − 500=0
25x=500
x=500/25=20
Interpretação: A raiz da função ocorre quando x=20. Isso significa que você precisa vender exatamente 20 ingressos para cobrir os custos do evento. A partir dessa quantidade, qualquer ingresso vendido gerará lucro
Exemplo 3: Planejamento Financeiro Pessoal
Considere que você esteja planejando suas finanças mensais. Suponha que você tenha um salário fixo de R$ 3.000,00 por mês, e você gasta R$ 200,00 em despesas variáveis para cada atividade extra que realiza (como jantares ou passeios). A função que descreve seu saldo S(x) ao final do mês, em função do número de atividades extras x, seria:
S(x)=3000 − 200x
Neste caso, o coeficiente angular a=−200 mostra que, quanto mais atividades você fizer, menor será o saldo ao final do mês. Se você fizer 8 atividades, seu saldo será:
S(8) = 3000 – 200(8) = 3000 – 1600 = R$ 1400,00
Essa função do primeiro grau ajuda a entender como suas despesas variáveis afetam suas finanças.
Exercícios Práticos de Funções do Primeiro Grau Aplicadas ao Cotidiano
1. Tarifa de Táxi em Outra Cidade
Em uma cidade vizinha, a tarifa dos táxis é composta por uma bandeirada de R$ 6,00 e um custo de R$ 3,50 por quilômetro rodado. Uma pessoa precisa fazer uma viagem de 10 km.
a) Crie uma fórmula que expressa o valor da tarifa T(x) em função dos quilômetros rodados xxx.
b) Calcule quanto essa pessoa pagará ao final da viagem.
Solução:
a) A fórmula para a tarifa é dada por: T(x)= 6,00 + 3,50x
b) Para x = 10 km:
T(10) = 6,00 + 3,50 .10 = 6,00 + 35,00 = R$ 41,00
Portanto, a pessoa pagará R$ 41,00.
2. Plano de Telefonia
Um plano de telefonia cobra uma taxa fixa mensal de R$ 30,00, mais R$ 0,50 por minuto de ligação. Um cliente usou 120 minutos de ligação em um mês.
a) Escreva uma função C(x) que representa o custo total em função dos minutos de ligação x.
b) Calcule o valor total da fatura desse cliente.
Solução:
a) A função do custo é:
C(x)=30,00 + 0,50x
b) Para x= 120 minutos:
C(120) = 30,00 + 0,50 . 120 = 30,00 + 60,00 = R$ 90,00
Portanto, o cliente pagará R$ 90,00.
3. Aluguel de Bicicletas
Uma loja de bicicletas cobra uma taxa fixa de R$ 15,00 para alugar uma bicicleta, mais R$ 5,00 por hora de uso. Um turista alugou uma bicicleta por 4 horas.
a) Encontre uma função A(x) que descreva o custo do aluguel em função das horas x.
b) Determine o custo total para o turista.
Solução:
a) A função para o custo do aluguel é:
A(x)=15,00 + 5,00x
b) Para x=4 horas:
A(4) = 15,00 + 5,00 . 4 = 15,00 + 20,00 = R$ 35,00
Portanto, o turista pagará R$ 35,00.
4. Conta de Água
Em uma cidade, a conta de água é composta por uma taxa fixa de R$ 25,00 e R$ 2,00 por metro cúbico de água consumido. Se uma família consumiu 15 metros cúbicos de água em um mês:
a) Escreva a função W(x) que descreve o valor da conta em função do consumo x.
b) Calcule a conta dessa família no mês.
Solução:
a) A função para o valor da conta é:
W(x)=25,00 + 2,00x
b) Para x=15 metros cúbicos:
W(15) = 25,00 + 2,00 . 15 = 25,00 + 30,00 = R$ 55,00
Portanto, a conta será de R$ 55,00.
5. Serviço de Streaming
Um serviço de streaming cobra R$ 20,00 de mensalidade e R$ 1,50 por filme assistido. Um usuário assistiu a 8 filmes no mês.
a) Formule a função S(x) que representa o custo total em função do número de filmes x.
b) Determine o valor total da fatura do usuário.
Solução:
a) A função do custo é:
S(x)=20,00 + 1,50x
b) Para x=8 filmes:
S(8) = 20,00 + 1,50 . 8 = 20,00 + 12,00 = R$ 32,00
Portanto, o usuário pagará R$ 32,00.
Conclusão
As funções do primeiro grau são ferramentas poderosas para modelar e resolver problemas do cotidiano. Compreender suas propriedades e saber aplicá-las em diferentes contextos pode simplificar a tomada de decisões, desde calcular custos e prever lucros até planejar financeiramente. A simplicidade e a versatilidade dessas funções fazem delas um recurso indispensável, tanto na matemática quanto na vida prática.













