Função Exponencial — Definição, Gráficos e Exercícios
Aprenda tudo sobre a função exponencial, suas propriedades, crescimento, decrescimento e como aplicá-la em problemas matemáticos e do dia a dia.
O que é uma Função Exponencial?
Uma função exponencial é aquela em que a variável aparece no expoente de uma base constante positiva e diferente de 1. Sua forma geral é dada por:
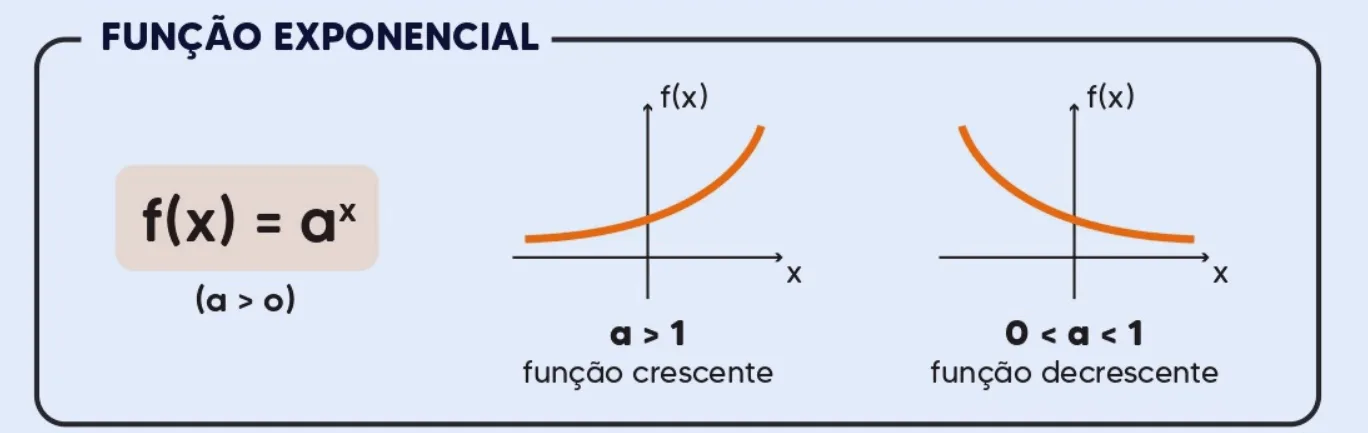
f(x) = ax, com a > 0 e a ≠ 1
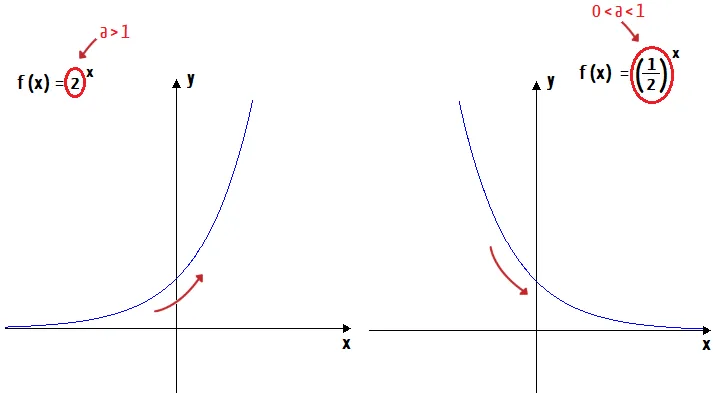
Isso significa que o comportamento da função depende do valor de a:
- a > 1 → a função é crescente.
- 0 < a < 1 → a função é decrescente.
Características da Função Exponencial
- O domínio é R (todos os números reais).
- A imagem é o conjunto dos números reais positivos (y > 0).
- O gráfico nunca toca o eixo x (assíntota horizontal em y = 0).
- Sempre passa pelo ponto (0, 1).
Função Exponencial Crescente
Quando a > 1, a função cresce conforme x aumenta. Exemplo:
f(x) = 2x
Nesse caso, f(x) cresce rapidamente: f(0)=1, f(1)=2, f(2)=4, f(3)=8…
Função Exponencial Decrescente
Quando 0 < a < 1, a função decresce conforme x aumenta. Exemplo:
f(x) = (1/2)x
Agora, quanto maior o valor de x, menor o resultado de f(x): f(0)=1, f(1)=1/2, f(2)=1/4, f(3)=1/8…
💡 Dica de Estudo
Aprofunde seus conhecimentos com o material Mapas Mentais de Matemática — ideal para revisar Funções e outros temas cobrados no ENEM e concursos.
Exemplos Práticos
Exemplo 1: Determine o valor de f(3) para f(x) = 2x.
Substituindo x = 3:
f(3) = 2³ = 8
Exemplo 2: Determine o valor de f(−2) para f(x) = (1/3)x.
Substituindo x = −2:
f(−2) = (1/3)−2 = 3² = 9
🔢 Exercícios Resolvidos
1) Calcule f(4) se f(x) = 3x.
f(4) = 3⁴ = 81
2) Encontre f(−1) para f(x) = 5x.
f(−1) = 5−1 = 1/5
🧮 Exercícios de Múltipla Escolha
3) Qual o valor de f(2) na função f(x) = 4x−1?
A) 2
B) 4
C) 8
D) 16
Resolução: f(2) = 42−1 = 4¹ = 4.
Alternativa correta: B.
4) O gráfico da função f(x) = (1/3)x é:
A) crescente
B) constante
C) decrescente
D) simétrico
Como 0 < 1/3 < 1, a função é decrescente.
Alternativa correta: C.
📘 Baixe seu eBook de Fórmulas Matemáticas
Tenha todas as fórmulas de funções, logaritmos e progressões reunidas em um só material gratuito!
👉 Clique aqui para baixar o eBook Fórmulas Matemática
Aplicações da Função Exponencial
A função exponencial aparece em diversas situações do cotidiano:
- Crescimento populacional — a população cresce exponencialmente com o tempo.
- Finanças — cálculo de juros compostos.
- Física — decaimento radioativo, resfriamento e reações químicas.
📚 Continue Aprendendo
Explore mais conteúdos relacionados:
ENEM Matemática |
10 eBooks de Matemática |
Banco de Questões













