As funções matemáticas são fundamentais na matemática e aparecem em diversas áreas, como cálculo, álgebra e análise. Entre as classificações mais importantes das funções, destacam-se as funções injetoras, sobrejetoras e bijetoras. Neste artigo, explicaremos cada uma delas, utilizando exemplos e diagramas para facilitar o entendimento.
O que é uma Função Injetora?
Uma função f: A → B é chamada de injetora quando elementos diferentes do domínio A possuem imagens diferentes no contradomínio B. Ou seja, se x1 ≠ x2, então f(x1) ≠ f(x2)
Exemplo de função injetora
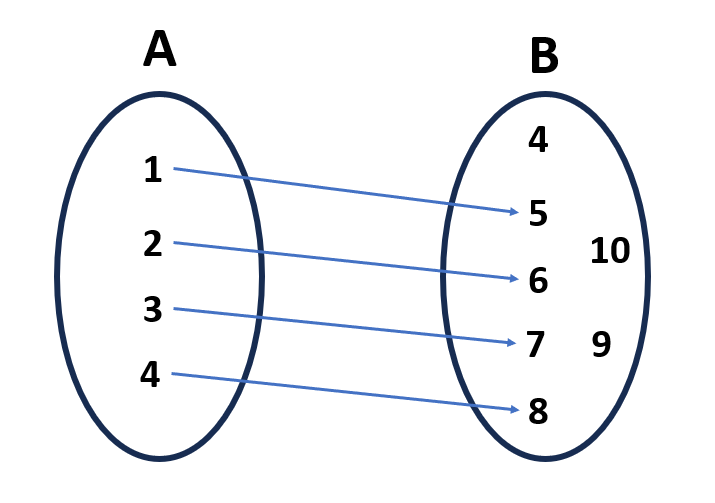
Considere o conjunto A={1, 2, 3, 4} e o conjunto B={4, 5, 6, 7, 8, 9, 10}. Se definirmos a função como:
f(1) = 5, f(2) = 6, f(3) = 7, f(4) =8
Podemos perceber que não há repetição de valores em B, ou seja, a função é injetora.
O que é uma Função Sobrejetora?
Uma função f: A → B é chamada de sobrejetora se todos os elementos do contradomínio BBB são atingidos por pelo menos um elemento do domínio AAA. Em outras palavras, a imagem da função deve ser igual ao contradomínio, ou seja, Im(f) = B.
Exemplo de função sobrejetora
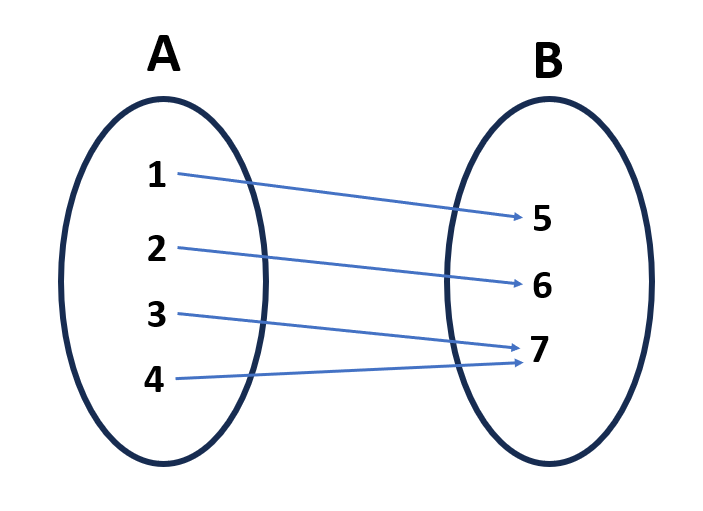
Considere o conjunto A={1, 2, 3, 4} e B={5, 6, 7}. Se a função for definida como:
f(1) =5, f(2) = 6, f(3) = 7, f(4) = 7
O elemento 7 recebe mais de uma correspondência, mas todos os elementos do conjunto BBB são atingidos. Logo, essa função é sobrejetora.
O que é uma Função Bijetora?
Uma função é chamada de bijetora quando é simultaneamente injetora e sobrejetora. Isso significa que:
- Cada elemento de A tem um único correspondente em BBB (função injetora);
- Todos os elementos de B são atingidos (função sobrejetora).
Dessa forma, para cada x ∈ A, existe exatamente um y ∈ B tal que f(x) = y.
Exemplo de função bijetora
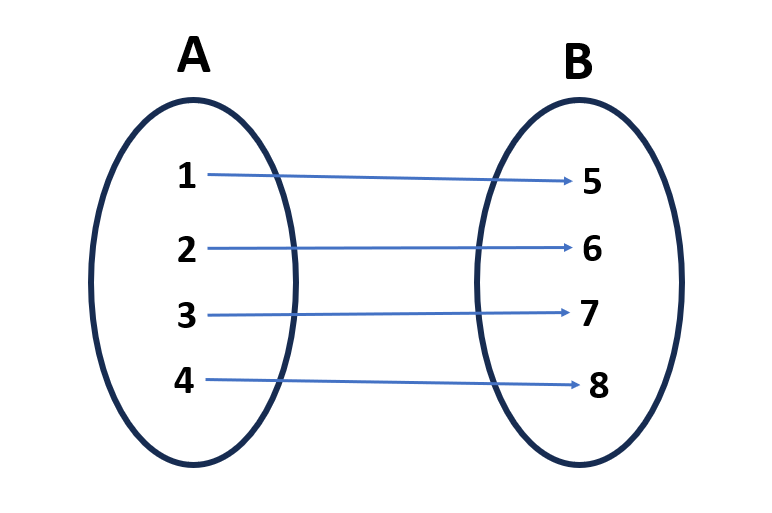
Considere os conjuntos A={1, 2, 3, 4} e B={5, 6, 7, 8}. Se a função for definida como:
f(1) = 5, f(2) = 6, f(3) = 7, f(4) = 8
Podemos notar que não há repetições em BBB e todos os elementos de BBB são atingidos. Portanto, essa função é bijetora.
Resumo das Classificações
Podemos resumir as três classificações com base nas seguintes regras:
- Função injetora: Não há repetição de valores em B.
- Função sobrejetora: Todos os elementos de B são atingidos.
- Função bijetora: É simultaneamente injetora e sobrejetora.
Essas funções são amplamente utilizadas em diversos contextos matemáticos, incluindo análise combinatória, probabilidade, e até mesmo na programação de computadores.
Esperamos que este artigo tenha esclarecido esses conceitos. Se tiver dúvidas, deixe seu comentário! 🚀
Lista de Exercício Função Injetora, Sobrejetora e Bijetora
Questão 1
Uma função f:A→Bf: A \to B é dita injetora quando:
A) Todo elemento do contradomínio é imagem de pelo menos um elemento do domínio.
B) Elementos distintos do domínio possuem imagens distintas no contradomínio.
C) Ela é sobrejetora e bijetora.
D) Admite uma função inversa, ou seja, se for inversível.
Resposta: B
Justificativa: A definição de função injetora estabelece que elementos distintos do domínio devem ter imagens distintas no contradomínio.
Questão 2
Dada a função f(x)=x2f(x) = x^2, podemos afirmar que ela será injetora se o domínio for:
A) Todos os números reais.
B) Todos os números inteiros.
C) Apenas os números naturais.
D) Todos os números racionais.
E) Essa função nunca será injetora.
Resposta: C
Justificativa: Para ser injetora, a função não pode ter valores de entrada diferentes gerando o mesmo valor de saída. Como f(x)=x2f(x) = x^2 não é injetora em R\mathbb{R} ou Z\mathbb{Z} (pois f(a)=f(−a)f(a) = f(-a)), restringindo-se ao domínio dos números naturais, cada valor de xx terá um único correspondente em BB, tornando a função injetora.
Questão 3
Dada a função f(x)=3x−4f(x) = 3x – 4 com domínio e contradomínio nos números reais, podemos afirmar que:
A) Se trata de uma função do 2º grau.
B) Se trata de uma função injetora.
C) f(20)=64f(20) = 64.
D) Se trata de uma função linear.
Resposta: B e D
Justificativa: A função f(x)=3x−4f(x) = 3x – 4 é uma função linear (não quadrática) e sempre crescente, garantindo que elementos distintos tenham imagens distintas, ou seja, é injetora.
Questão 4
Dada a função f(x)=∣3x+2∣f(x) = |3x + 2|, analise as afirmações:
I – Essa função é injetora.
II – f(1)=f(−1)f(1) = f(-1).
III – A imagem dessa função são os números reais positivos.
Marque a alternativa correta:
A) Somente a afirmativa I é verdadeira.
B) Somente a afirmativa II é verdadeira.
C) Somente a afirmativa III é verdadeira.
D) Todas as afirmativas são falsas.
Resposta: B
Justificativa: Como a função f(x)=∣3x+2∣f(x) = |3x + 2| envolve módulo, ela não pode ser injetora, pois há valores distintos de xx que geram a mesma imagem. Afirmativa II está correta porque f(1)=f(−1)f(1) = f(-1), e a afirmativa III está errada, pois a imagem inclui o zero.
Questão 5
Dada a função f(x)=x2−2f(x) = x^2 – 2, com domínio A={0,1,2,3}A = \{0,1,2,3\} e contradomínio B={−2,−1,2,7}B = \{-2,-1,2,7\}, podemos afirmar que:
A) A função é inversível, pois é bijetora.
B) A função não é inversível, pois é injetora, mas não sobrejetora.
C) A função não é inversível, pois é sobrejetora, mas não injetora.
D) A função não é inversível, pois é bijetora.
Resposta: C
Justificativa: A função f(x)=x2−2f(x) = x^2 – 2 pode ser sobrejetora se todos os elementos do contradomínio forem atingidos, mas não é injetora pois f(a)=f(−a)f(a) = f(-a).
Questão 6
A função f(x,y)=x−yf(x, y) = x – y, com A={(1,2),(1,1),(2,1),(5,3)}A = \{(1,2), (1,1), (2,1), (5,3)\} e B={−1,0,1,2,3}B = \{-1,0,1,2,3\}, é classificada como:
A) Afim.
B) Injetora.
C) Sobrejetora.
D) Bijetora.
E) Exponencial.
Resposta: B
Justificativa: Para cada par (x,y)(x,y), temos um único resultado em BB, garantindo que seja injetora, pois elementos diferentes geram imagens distintas.
Questão 7
No contexto de uma quadrilha junina, foram formados 12 pares distintos entre 12 meninas e 13 meninos. Podemos classificar a função que associa cada menina a um menino como:
A) Injetora
B) Sobrejetora
C) Bijetora
D) Nenhuma das anteriores
Resposta: A
Justificativa: Cada menina tem um par diferente, mas há um menino sem par, o que impede a sobrejetividade.
Questão 8
Considere a função f:A→Bf: A \to B que associa cada número inteiro xx ao seu sucessor x+1x+1. Essa função é:
A) Apenas injetora
B) Apenas sobrejetora
C) Bijetora
D) Nenhuma das anteriores
Resposta: C
Justificativa: A função define uma relação um para um e cobre todos os números do contradomínio, tornando-a bijetora.
Questão 9
Se f(x)=x3f(x) = x^3, essa função é:
A) Apenas injetora
B) Apenas sobrejetora
C) Bijetora
D) Nenhuma das anteriores
Resposta: C
Justificativa: A função cúbica não gera valores repetidos e cobre todos os reais, garantindo bijetividade.
Questão 10
A função f(x)=exf(x) = e^x é:
A) Apenas injetora
B) Apenas sobrejetora
C) Bijetora
D) Nenhuma das anteriores
Resposta: A
Justificativa: A função exponencial é sempre crescente, garantindo injetividade, mas nunca assume valores negativos, impedindo sobrejetividade.
Caso precise de ajustes ou mais questões, me avise! 🚀













