Função Quadrática: A Importância de Estudar por Exercícios

A função quadrática, também conhecida como função do 2º grau, é um dos conceitos mais importantes da matemática. Suas aplicações vão desde problemas geométricos até questões financeiras e físicas, como o cálculo de trajetórias. Embora a teoria seja fundamental, o domínio real desse tema vem com a prática por meio de exercícios de função quadrática.

O Que é uma Função Quadrática?

A função quadrática é definida pela fórmula geral:

f(x) = ax² + bx + c

Onde:

• (a): Coeficiente principal (a ≠ 0) – determina a concavidade da parábola.
• (b): Coeficiente linear – influencia o deslocamento do gráfico.
• (c): Termo constante – indica onde o gráfico cruza o eixo (y).

Características da Função Quadrática

1. Gráfico em Forma de Parábola:

• Concavidade voltada para cima ((a > 0)).
• Concavidade voltada para baixo ((a < 0)).

1. Vértice:
   O ponto mais alto ou mais baixo da parábola, dado por:
   
   xv = -b/2a}=, = yv = f(x_v)
   
2. Raízes ou Zeros da Função:
   Pontos onde o gráfico cruza o eixo (x), obtidos resolvendo (ax² + bx + c = 0), com a fórmula de Bhaskara:

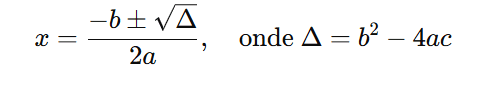
Por Que Estudar Função Quadrática por Exercícios?

1. Fixação dos Conceitos

Resolver exercícios de função quadrática ajuda a entender a relação entre os coeficientes e o formato do gráfico.

2. Aplicação Prática

As funções quadráticas são usadas para modelar situações reais, como:

• Cálculo de trajetórias (movimento parabólico).
• Análise de lucros e custos.
• Otimização de recursos.

3. Preparação para Provas

A função quadrática é um tema recorrente em vestibulares e concursos, sendo frequentemente aplicada em questões contextualizadas.

4. Desenvolvimento do Raciocínio Lógico

Resolver exercícios exige a interpretação de gráficos, aplicação de fórmulas e análise de resultados, fortalecendo o raciocínio matemático.

Estratégias para Estudar Função Quadrática

1. Entenda os Conceitos Básicos: Revise a fórmula geral, o cálculo do vértice e a fórmula de Bhaskara.
2. Pratique com Gráficos: Analise como as mudanças nos coeficientes ((a), (b), (c)) afetam o formato da parábola.
3. Resolva Problemas Aplicados: Trabalhe com questões que envolvam contextos reais, como lucro máximo ou altura de projéteis.
4. Interprete os Resultados: Além de resolver, entenda o significado dos valores obtidos no contexto do problema.

Benefícios de Resolver Exercícios de Função Quadrática

1. Aplicabilidade Prática

Resolver exercícios de função quadrática permite modelar situações como:

• O tempo e a altura de um objeto lançado para cima.
• O lucro máximo de uma empresa com base em seus custos e receitas.
• O alcance de um projétil.

2. Melhora no Raciocínio Analítico

A prática constante desenvolve sua habilidade de interpretar dados e aplicar conceitos matemáticos.

3. Confiança em Provas

Resolver exercícios variados aumenta sua familiaridade com o tema e confiança para lidar com questões em avaliações.

Dicas para Resolver Exercícios de Função Quadrática

1. Identifique os Coeficientes: Reconheça os valores de (a), (b) e (c) na equação antes de começar a resolver.
2. Use a Fórmula de Bhaskara com Atenção: Calcule o discriminante ((\Delta)) corretamente para determinar o número de raízes.
3. Interprete o Vértice: O vértice pode indicar o ponto máximo ou mínimo da função, dependendo do sinal de (a).
4. Pratique Regularmente: Resolva exercícios que envolvam gráficos, cálculos de raízes e aplicações em problemas do dia a dia.

Exemplos de Aplicação

Resolver exercícios de função quadrática ajuda a compreender aplicações práticas, como:

• Movimento Parabólico: Um projétil lançado verticalmente alcança a altura máxima em 3 segundos. Qual a altura máxima?
• Lucro Máximo: Uma empresa tem custos e receitas modelados por (f(x) = -2x² + 8x + 12). Qual o lucro máximo?
• Trajetória: Um jogador de basquete arremessa uma bola, e a altura da bola em função do tempo é (h(t) = -5t² + 20t + 2). Qual o tempo para atingir a altura máxima?

Esses exercícios mostram como a função quadrática é prática e essencial.

🟢Acesse a lista aqui

Conclusão

A função quadrática é uma ferramenta poderosa e indispensável na matemática. Resolver exercícios de função quadrática é fundamental para consolidar o aprendizado, interpretar gráficos e se preparar para aplicações práticas e provas.

Pronto para começar? Explore exercícios variados, contextualizados e desafiadores, e veja como sua compreensão e confiança evoluem com a prática. Bons estudos! 🚀