Geometria Analítica: A Importância de Estudar por Exercícios

A geometria analítica é uma área da matemática que une álgebra e geometria para estudar figuras geométricas no plano cartesiano. Com aplicações em física, engenharia, economia e muitas outras áreas, ela é indispensável para quem busca entender como as formas se relacionam com números. Embora os conceitos teóricos sejam fundamentais, o domínio da geometria analítica só é alcançado por meio da prática com exercícios de geometria analítica.

O Que é Geometria Analítica?

A geometria analítica utiliza o sistema cartesiano para representar pontos, linhas, curvas e superfícies em termos de equações algébricas. Entre os principais elementos estudados, destacam-se:

Conceitos Básicos

Pontos no Plano:
Um ponto no plano cartesiano é representado por suas coordenadas ((x, y)).

Distância Entre Dois Pontos:
A distância entre os pontos A(x1, y1) e B(x2, y2) é calculada por:

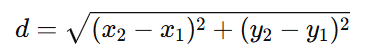
Ponto Médio:
O ponto médio entre (A(x1, y1)) e (B(x2, y2)) é dado por:

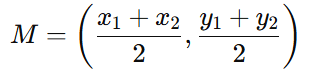
Equação da Reta:
A equação geral da reta é:

ax + by + c = 0

E sua forma reduzida (inclinação linear):

y = mx + n

Onde:

• (m): Coeficiente angular (declividade da reta).
• (n): Intercepto no eixo (y).

1. Circunferência:
   A equação da circunferência com centro em C(h, k) e raio (r) é:
   
   (x – h)² + (y – k)² = r²
   

Por Que Estudar Geometria Analítica por Exercícios?

1. Fixação dos Conceitos

Resolver exercícios de geometria analítica ajuda a entender como aplicar fórmulas e relacionar coordenadas com formas geométricas.

2. Aplicação em Situações Reais

A geometria analítica é usada para modelar problemas reais, como:

• Planejamento de trajetórias.
• Posicionamento de objetos no espaço.
• Análise de mapas e gráficos.

3. Preparação para Provas

Os conceitos de geometria analítica são amplamente cobrados em vestibulares e concursos, sendo necessários para resolver questões geométricas e algébricas.

4. Desenvolvimento do Raciocínio Lógico

Resolver problemas de geometria analítica exige combinar análise geométrica e habilidades algébricas, fortalecendo o pensamento lógico.

Estratégias para Estudar Geometria Analítica

1. Domine os Conceitos Básicos: Comece com distância, ponto médio e equações de retas antes de avançar para figuras mais complexas.
2. Pratique Com Gráficos: Representar as equações no plano ajuda a visualizar os problemas.
3. Estude Casos Aplicados: Resolva problemas que envolvam figuras geométricas, áreas e interseções.
4. Verifique as Soluções: Sempre substitua os valores encontrados nas equações para garantir que são válidos.

Benefícios de Resolver Exercícios de Geometria Analítica

1. Aplicabilidade Prática

Resolver exercícios de geometria analítica prepara você para compreender situações como:

• Localização de pontos em um espaço cartesiano.
• Análise de trajetórias e distâncias.
• Determinação de áreas e interseções de figuras geométricas.

2. Melhora no Raciocínio Analítico

A prática constante desenvolve sua habilidade de combinar geometria e álgebra de forma eficiente.

3. Confiança em Provas

Resolver muitos exercícios aumenta sua familiaridade com os tipos de questões cobradas e confiança para resolvê-las.

Dicas para Resolver Exercícios de Geometria Analítica

1. Organize os Dados: Sempre identifique e anote as coordenadas dos pontos e as equações fornecidas.
2. Use Diagramas: Representar os pontos e linhas no plano cartesiano pode ajudar a interpretar problemas mais complexos.
3. Simplifique as Equações: Reorganize equações de retas, circunferências e outras figuras para facilitar os cálculos.
4. Pratique Regularmente: Resolva uma variedade de exercícios, incluindo problemas práticos e contextuais.

Exemplos de Aplicação

Resolver exercícios de geometria analítica ajuda a entender situações como:

• Trajetória de um Objeto: Determinar se uma linha cruza um determinado ponto.
• Distância entre Pontos: Calcular a menor distância entre dois locais em um mapa.
• Interseção de Figuras: Descobrir onde duas retas ou uma reta e uma circunferência se encontram.

Esses exercícios mostram como a geometria analítica é prática e indispensável.

🟢Acesse a lista de exercício aqui

Conclusão

A geometria analítica é uma ferramenta poderosa para compreender e resolver problemas geométricos e algébricos. Resolver exercícios de geometria analítica é indispensável para consolidar conceitos, interpretar gráficos e se preparar para aplicações práticas e provas.

Pronto para começar? Pratique com questões variadas, contextualizadas e desafiadoras, e veja como sua compreensão e confiança evoluem com a prática. Bons estudos! 🚀