Hipérbole: Um Guia Completo

A hipérbole é uma curva aberta formada pela interseção de um plano com um cone duplo em um ângulo maior que o da geratriz do cone. Ao contrário da elipse e da parábola, a hipérbole tem duas partes chamadas ramos, que se afastam indefinidamente uma da outra. Este artigo aborda os principais conceitos, notações e equações relacionados à hipérbole, focando nas definições geométricas e analíticas.

1. Componentes da Hipérbole

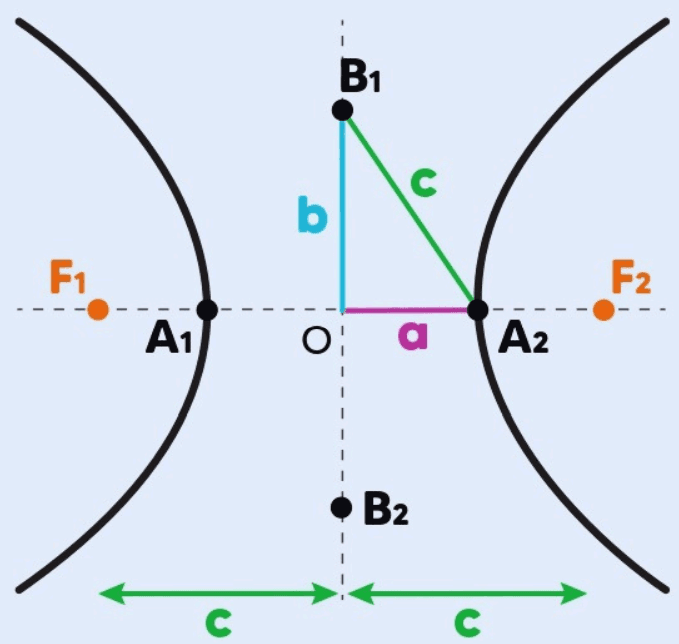
• Centro (O): O ponto médio do segmento que une os dois focos (F₁ e F₂). Este ponto é o ponto de simetria da hipérbole.
• Focos (F₁ e F₂): Dois pontos fixos F₁ e F₂ tais que a diferença das distâncias de qualquer ponto P da hipérbole a esses dois focos é constante e igual a 2a.
• Eixo Real ou Transversal (A₁A₂): É o eixo que passa pelos focos F₁ e F₂. A distância entre os vértices da hipérbole, A₁ e A₂, é igual a 2a, onde ‘a’ é a semi-distância do eixo real.
• Eixo Imaginário (B₁B₂): É o eixo perpendicular ao eixo real que passa pelo centro O. A distância entre os extremos do eixo imaginário, B₁ e B₂, é igual a 2b, onde ‘b’ é a semi-distância do eixo imaginário.

2. Propriedades da Hipérbole

• Relação entre os eixos:
  
• onde ‘c’ é a distância do centro O a cada foco F₁ ou F₂.
• Excentricidade (e):
  A excentricidade da hipérbole é definida como a razão entre a distância focal e a semi-distância do eixo real:
  
• Como ( c > a ) em uma hipérbole, a excentricidade será sempre maior que 1.

3. Equação da Hipérbole

A equação da hipérbole depende da orientação do eixo real.

Hipérbole com Eixo Real Horizontal

Quando o eixo real A₁A₂ é horizontal, a equação da hipérbole é dada por:

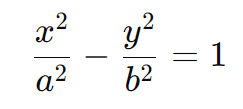
Aqui, o centro da hipérbole está na origem (0, 0), os focos estão localizados em (±c, 0), e os vértices em (±a, 0).

As Assíntotas da Hipérbole Eixo Real Horizontal

As assíntotas de uma hipérbole são retas que passam pelo centro O e definem a direção dos ramos da hipérbole. Para uma hipérbole com eixo real horizontal, as equações das assíntotas são:

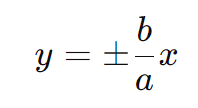
As assíntotas ajudam a definir o formato e a direção dos ramos da hipérbole.

Exemplo: Considere uma hipérbole com centro em O(0,0), onde a semi-distância do eixo real é a=4 e a semi-distância do eixo imaginário é b=3. Encontre a equação da hipérbole, as coordenadas dos focos, dos vértices e as equações das assíntotas.

Solução: Equação da Hipérbole

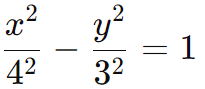
Simplificando:

Coordenadas dos Focos:

Para identificar o foco, calculamos a distância focal c usando a relação:

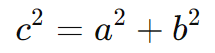
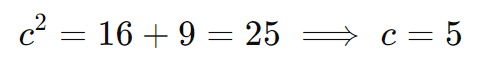
Como o eixo real é horizontal, os focos estão em (±c, 0), ou seja:

F1(5,0) e F2(−5,0)

Coordenadas dos Vértices:

Os vértices estão em (±a, 0), ou seja:

A₁(4,0) e A₂(−4,0)

Equações das Assíntotas:

Ou seja, as assíntotas são:

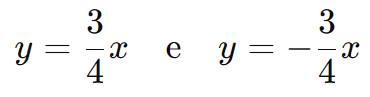
Hipérbole com Eixo Real Vertical

Quando o eixo real A1A2 é vertical, a equação da hipérbole é dada por:

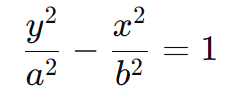
Neste caso, o centro da hipérbole está na origem (0, 0), os focos estão localizados em (0, ±c), e os vértices em (0, ±a).

As Assíntotas da Hipérbole Eixo Real Vertical

As assíntotas de uma hipérbole são retas que passam pelo centro O e definem a direção dos ramos da hipérbole. Para uma hipérbole com eixo real vertical, as equações das assíntotas são:

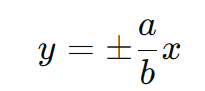
As assíntotas ajudam a definir o formato e a direção dos ramos da hipérbole.

Exemplo: Considere uma hipérbole com centro em O(0,0), onde a semi-distância do eixo real é a=5 e a semi-distância do eixo imaginário é b=2. Encontre a equação da hipérbole, as coordenadas dos focos, dos vértices e as equações das assíntotas.

Solução:

Equação da Hipérbole:

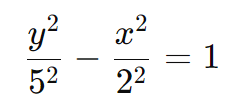
Simplificando:

Coordenadas dos Focos:

Primeiro, calculamos a distância focal c usando a relação:

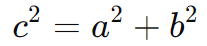
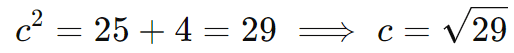
Como o eixo real é vertical, os focos estão em (0, ±c), ou seja:

F₁(0, √29) e F₂(0,−√29)

Coordenadas dos Vértices:

Os vértices estão em (0, ±a), ou seja:

A₁(0,5) e A₂(0,−5)

Equações das Assíntotas:

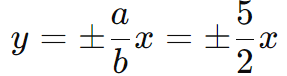
Ou seja, as assíntotas são:

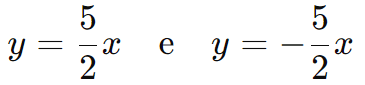
Hipérbole com Centro O(x₀,y₀)

Hipérbole com Eixo Real Horizontal

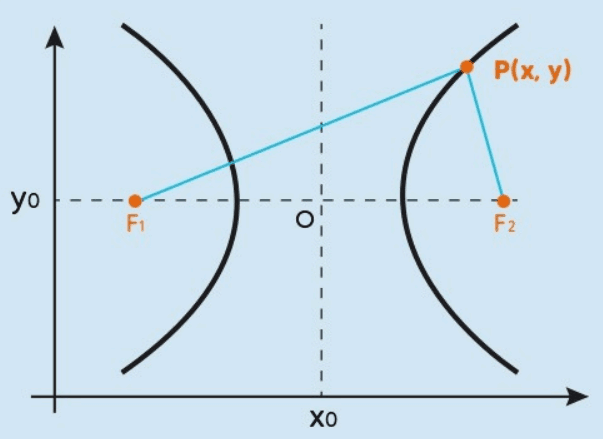
Se o eixo real A₁A₂ for horizontal e o centro O estiver em (x₀,y₀), a equação da hipérbole é dada por:

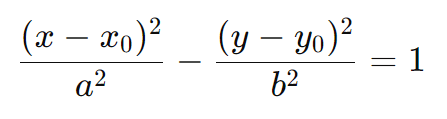
Aqui, os focos estarão localizados em (x₀±c, y₀), e os vértices em (x₀±a, y₀).

As equações das assíntotas também se ajustam ao centro O(x₀,y₀).

Assíntotas da Hipérbole com Eixo Real Horizontal

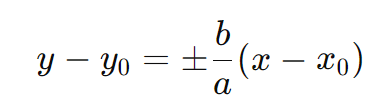
As assíntotas ajudam a definir o formato e a direção dos ramos da hipérbole.

Exemplo: Considere a hipérbole com centro em O(2,−1), onde a semi-distância do eixo real é a=3 e a semi-distância do eixo imaginário é b=4. Encontre a equação da hipérbole, as coordenadas dos focos, dos vértices e as equações das assíntotas.

Solução: Equação da Hipérbole

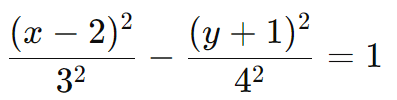
Simplificando:

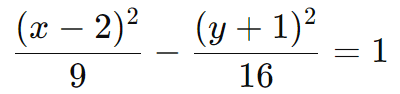
Coordenadas dos Focos:

Primeiro, calculamos a distância focal c usando a relação:

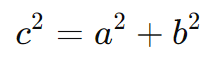
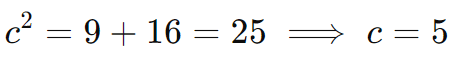
Como o eixo real é horizontal, os focos estão em (x₀±c, y₀), ou seja:

F₁(2+5, −1) = F₁(7, −1) e F₂(2−5, −1) = F₂(−3, −1)

Coordenadas dos Vértices:

Os vértices estão em (x₀±a, y₀), ou seja:

A₁(2+3,−1) = A₁(5,−1) e A₂(2−3, −1) = A₂(−1, −1)

Equações das Assíntotas:

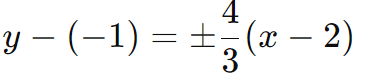
Simplificando:

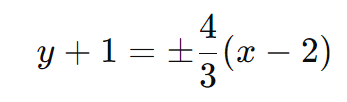
ou

2. Hipérbole com Eixo Real Vertical

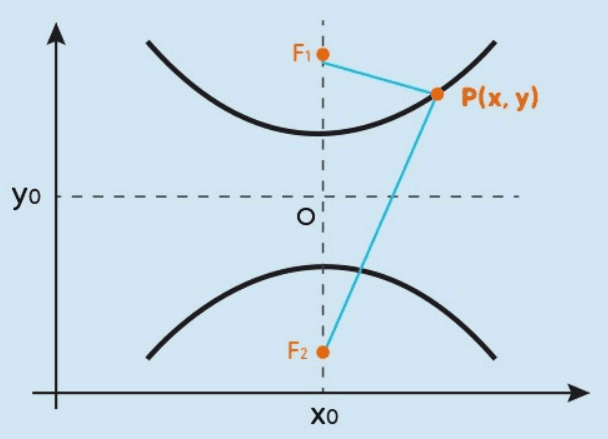
Se o eixo real A₁A₂ for vertical e o centro O estiver em(x₀,y₀), a equação da hipérbole é dada por:

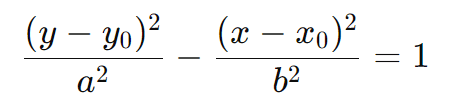
Neste caso, os focos estarão localizados em (x₀, y₀±c), e os vértices em (x₀, y₀±a).

As equações das assíntotas também se ajustam ao centro O(x₀,y₀).

Assíntotas da Hipérbole Hipérbole com Eixo Real Vertical

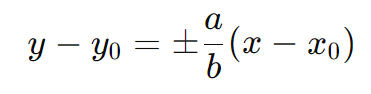
As assíntotas ajudam a definir o formato e a direção dos ramos da hipérbole.

Exemplo: Considere a hipérbole com centro em O(−2,3)O(-2, 3)O(−2,3), onde a semi-distância do eixo real é a=4a = 4a=4 e a semi-distância do eixo imaginário é b=2b = 2b=2. Encontre a equação da hipérbole, as coordenadas dos focos, dos vértices e as equações das assíntotas.

Solução: Equação da Hipérbole

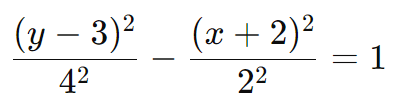
Simplificando:

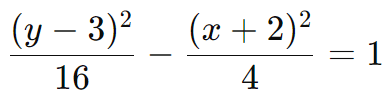
Coordenadas dos Focos:

Primeiro, calculamos a distância focal c usando a relação:

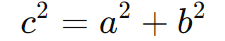
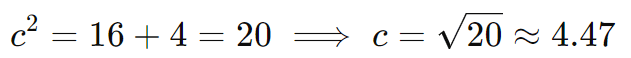
Como o eixo real é vertical, os focos estão em (x₀, y₀±c), ou seja:

Como o eixo real é vertical, os focos estão em (x₀, y₀±c), ou seja:

F₁(−2; 3+4,47)≈ F₁(−2; 7,47) e F₂(−2; 3−4,47) ≈ F₂(−2; −1,47)

Coordenadas dos Vértices:

Os vértices estão em (x₀, y₀±a), ou seja:

A₁(−2, 3+4) = A₁(−2, 7) e A₂(−2, 3−4) = A₂(−2, −1)

Equações das Assíntotas:

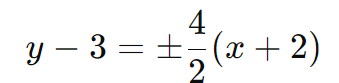
Simplificando:

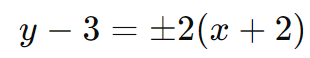
ou

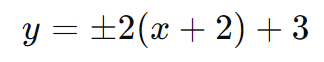
Considerações Finais

A hipérbole é uma das cônicas mais fascinantes da matemática, com aplicações em diversos campos como a astronomia, a física e a engenharia. Compreender suas propriedades e equações é essencial para estudar e aplicar conceitos geométricos em problemas complexos.

Este artigo forneceu uma visão detalhada sobre as notações e equações fundamentais da hipérbole, abordando tanto o eixo real horizontal quanto o vertical, além de suas assíntotas. Com este conhecimento, você estará bem equipado para explorar mais profundamente as aplicações da hipérbole em diferentes áreas.

Leia também

Geometria Analítica: Pontos ⇒ Distância, Ponto Médio e Colinearidade

Distância entre Retas e Cálculo da Área de um Triângulo

Circunferência: Equação Geral e Reduzida

A Parábola: Definição, Propriedades e Equações 

Elipse: Conceito, Propriedades e Equações

Hipérbole: Um Guia Completo