O histograma é um dos gráficos mais utilizados em estatística para representar a distribuição de variáveis quantitativas contínuas. Ele utiliza barras retangulares para mostrar como os dados estão distribuídos em intervalos de classe, permitindo identificar padrões e tendências de forma visual.
1. O Que é um Histograma?
Um histograma é um gráfico de barras onde:
- O eixo horizontal (x) representa os intervalos de classe (faixas de valores).
- O eixo vertical (y) mostra as frequências absolutas, relativas ou percentuais de cada intervalo.
- As barras são contínuas, sem espaçamento entre elas, refletindo a continuidade dos dados.
2. Características do Histograma
- Representação de Dados Contínuos: Ideal para variáveis mensuráveis, como altura, peso e tempo.
- Intervalos de Classe: Os dados são agrupados em faixas (intervalos), cada uma com a mesma amplitude.
- Altura das Barras: Proporcional à frequência dos dados no intervalo correspondente.
- Identificação de Padrões: Permite observar a forma da distribuição (simétrica, assimétrica, unimodal, multimodal, etc.).
3. Quando Usar um Histograma?
- Para representar dados contínuos agrupados em intervalos de classe.
- Quando se deseja visualizar a distribuição dos dados.
- Para identificar concentrações e tendências em grandes conjuntos de dados.
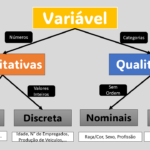
4. Qual a Diferença entre o Histograma e o Gráfico de Barras?
Embora o histograma e o gráfico de barras sejam visualmente semelhantes, eles possuem diferenças significativas:
| Critério | Histograma | Gráfico de Barras |
|---|---|---|
| Orientação das Barras | Contínuas (sem espaçamento entre as barras) | Espaçadas (há um intervalo entre as barras) |
| Dados Representados | Dados contínuos (agrupados em intervalos de classe) | Dados qualitativos ou quantitativos discretos |
| Objetivo | Mostrar a distribuição de uma variável | Comparar categorias ou valores individuais |
| Eixo Horizontal (x) | Intervalos de classe | Categorias ou valores |
Exemplo:
- Um histograma pode ser usado para representar a distribuição das alturas de uma população.
- Um gráfico de barras seria mais apropriado para comparar a frequência de preferências de cores.
5. Construção de um Histograma
Exemplo Prático 1: Tempo de Lazer Diário
Cenário:
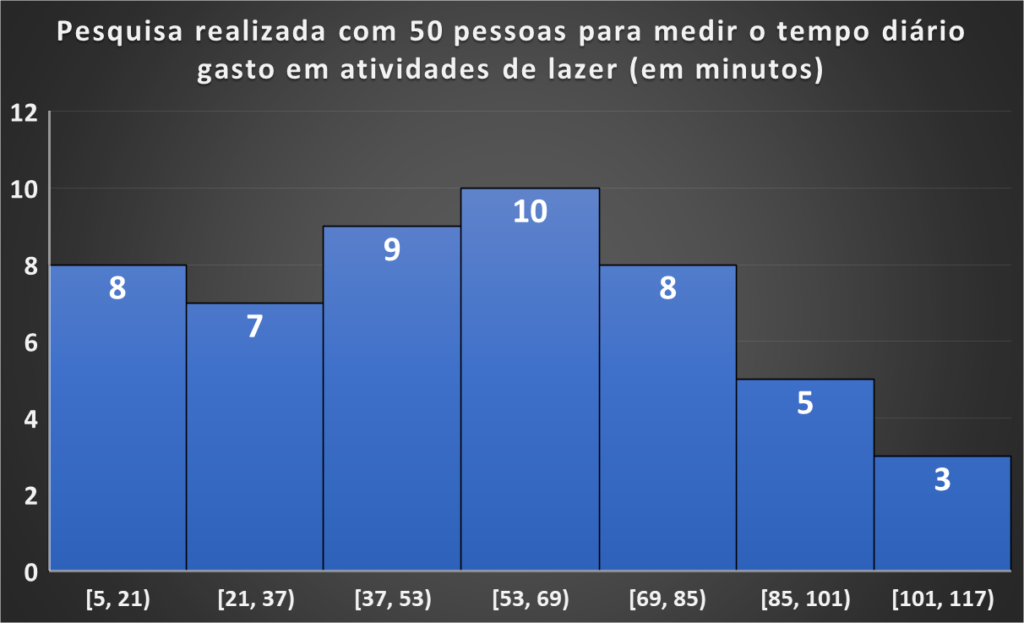
Uma pesquisa foi realizada com 50 pessoas para medir o tempo diário gasto em atividades de lazer (em minutos). Os dados e passos para a construção do histograma foram apresentados anteriormente.
Dados Brutos (em minutos):
45, 30, 50, 65, 40, 35, 60, 55, 70, 80, 75, 50, 45, 90, 85, 95, 100, 110, 115, 120, 50, 55, 65, 70, 75, 80, 85, 90, 95, 60, 40, 35, 30, 25, 20, 15, 50, 55, 60, 45, 30, 25, 20, 15, 10, 5, 100, 105, 110, 115.
Passo 1: Organizar o Rol
Os dados em ordem crescente:
5, 10, 15, 15, 20, 20, 25, 25, 30, 30, 30, 35, 35, 40, 40, 45, 45, 45, 50, 50, 50, 50, 55, 55, 55, 60, 60, 60, 65, 65, 70, 70, 75, 75, 75, 80, 80, 85, 85, 85, 90, 90, 95, 95, 100, 100, 105, 110, 110, 115.
Passo 2: Calcular a Amplitude Total e o Número de Classes
Amplitude Total (AT):
AT = Maior valor − Menor valor = 115 − 5 = 110 minutos
Número de Classes (k): Usando a regra de Sturges:
k = 1 + 3.3⋅log10(50) ≈ 6.6
Arredondamos para 7 classes.
Amplitude de Cada Classe (AC):
AC = AT/k = 110/7 ≈ 15,7 minutos
Arredondamos para 16 minutos.
Passo 3: Definir os Intervalos de Classe
Os intervalos são definidos a partir do menor valor (5 minutos) e incrementam pela amplitude de 16 minutos:
- [5, 21)
- [21, 37)
- [37, 53)
- [53, 69)
- [69, 85)
- [85, 101)
- [101, 117)
Passo 4: Calcular as Frequências
Contamos os dados dentro de cada intervalo:
| Intervalo (min) | Frequência Absoluta (ni) | Frequência Relativa (%) |
|---|---|---|
| [5, 21) | 8 | (8/50)⋅100 = 16,0% |
| [21, 37) | 7 | (7/50)⋅100 = 14,0% |
| [37, 53) | 9 | (9/50)⋅100 = 18,0% |
| [53, 69) | 10 | (10/50)⋅100 = 20,0% |
| [69, 85) | 8 | (8/50)⋅100 = 16,0% |
| [85, 101) | 5 | (5/50)⋅100 = 10,0% |
| [101, 117) | 3 | (3/50)⋅100 = 6,0% |
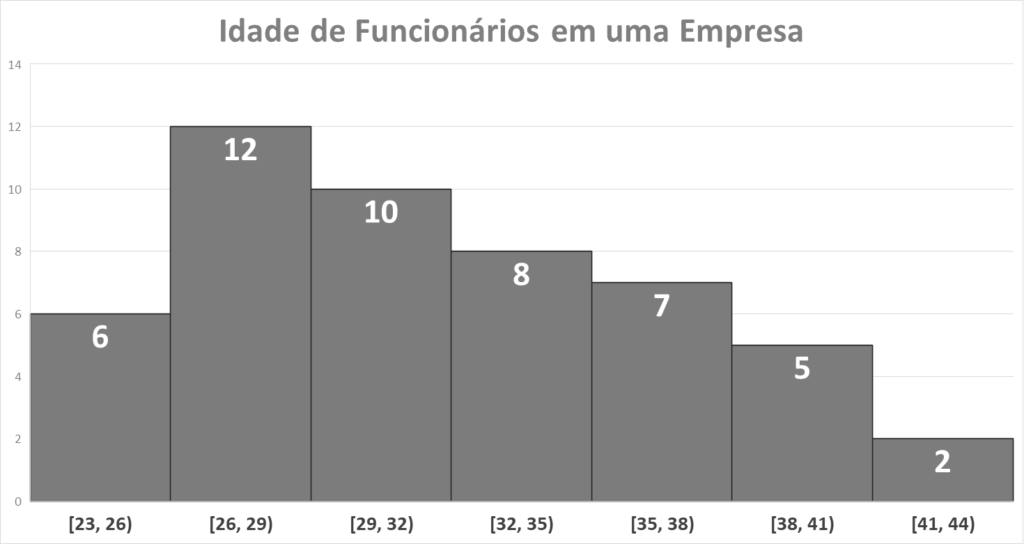
Exemplo Adicional: Idade de Funcionários em uma Empresa
Cenário
Uma empresa realizou um levantamento das idades de 50 funcionários. Os dados coletados (em anos) são:
Dados Brutos (em anos):
23, 25, 27, 30, 32, 35, 28, 26, 34, 29, 31, 33, 25, 24, 26, 27, 30, 32, 35, 36, 29, 28, 34, 33, 31, 37, 39, 38, 40, 41, 42, 35, 33, 32, 28, 27, 30, 29, 40, 38, 37, 36, 34, 35, 25, 31, 39, 42, 41, 40.
Passo 1: Organizar o Rol
Os dados em ordem crescente:
23, 24, 25, 25, 25, 26, 26, 27, 27, 27, 28, 28, 28, 29, 29, 29, 30, 30, 30, 31, 31, 31, 32, 32, 32, 33, 33, 33, 34, 34, 34, 35, 35, 35, 35, 35, 36, 36, 37, 37, 38, 38, 39, 39, 40, 40, 40, 41, 41, 42.
Passo 2: Calcular a Amplitude Total e o Número de Classes
Amplitude Total (AT):
AT = Maior valor − Menor valor = 42 − 23 = 19 anos
Número de Classes (k): Usando a regra de Sturges:
k = 1 + 3.3⋅log10(50) ≈ 6.6
Arredondamos para 7 classes.
Amplitude de Cada Classe (AC):
AC = AT/k =19/7 ≈ 2.71 anos
Arredondamos para 3 anos para simplificar.
Passo 3: Definir os Intervalos de Classe
Os intervalos de classe são definidos a partir do menor valor (23 anos), incrementando a amplitude de 3 anos:
- [23, 26)
- [26, 29)
- [29, 32)
- [32, 35)
- [35, 38)
- [38, 41)
- [41, 44)
Passo 4: Calcular as Frequências
Contamos os dados dentro de cada intervalo:
| Intervalo (anos) | Frequência Absoluta (ni) | Frequência Relativa (%) |
|---|---|---|
| [23, 26) | 6 | (6/50)⋅100 = 12,0% |
| [26, 29) | 12 | (12/50)⋅100 = 24,0% |
| [29, 32) | 10 | (10/50)⋅100 = 20,0% |
| [32, 35) | 8 | (8/50)⋅100 = 16,0% |
| [35, 38) | 7 | (7/50)⋅100 = 14,0% |
| [38, 41) | 5 | (5/50)⋅100 = 10,0% |
| [41, 44) | 2 | (2/50)⋅100 = 4,0% |

Interpretação do Histograma
- Distribuição: A maior concentração de idades está no intervalo [26, 29), que corresponde a 24% dos funcionários.
- Forma: A distribuição é levemente assimétrica à esquerda, indicando que há uma leve concentração em idades menores.
- Tendências: Apenas 4% dos funcionários têm idade acima de 41 anos.
6. Conclusão
O histograma é uma ferramenta essencial para análise estatística descritiva, permitindo a visualização da distribuição de variáveis contínuas. Com passos simples, como organização do rol, definição de intervalos e contagem de frequências, é possível construir um gráfico claro e informativo. Use o histograma para explorar e compreender melhor os dados antes de avançar para análises mais complexas.