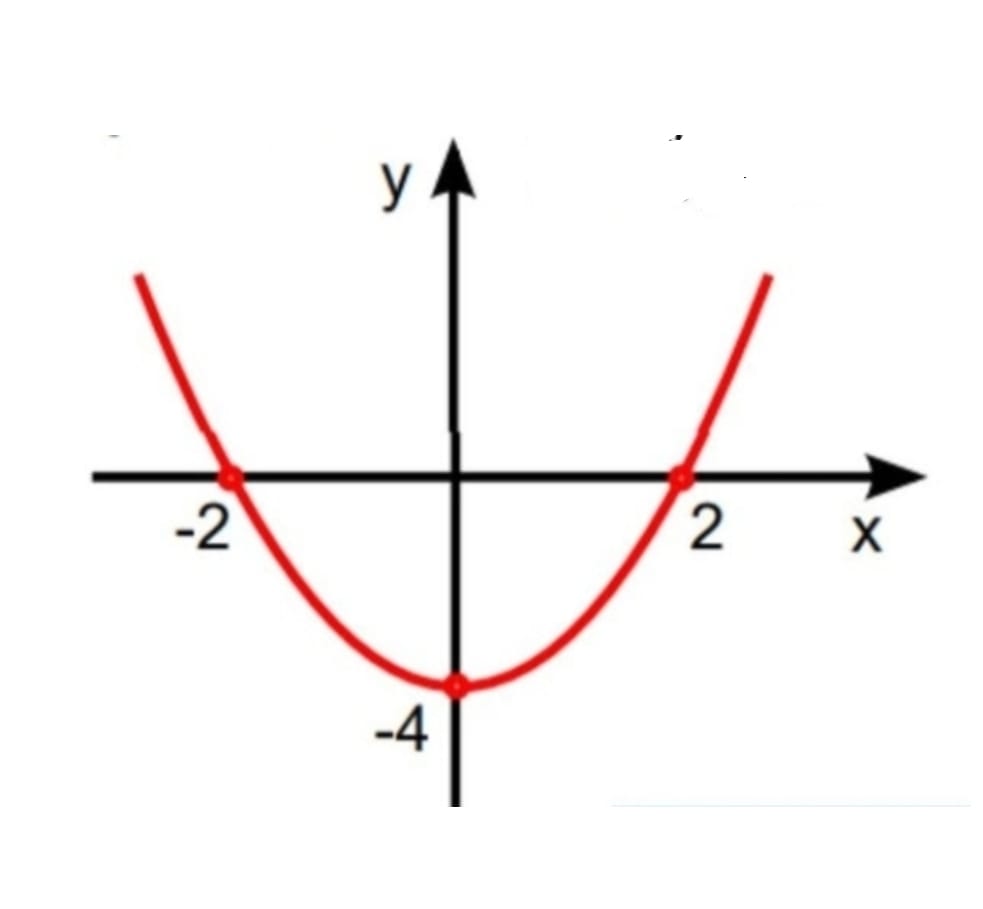
Dada a parábola representada no plano cartesiano, identifique a função que a define. Considere as opções abaixo:

a) y=x² + 4
b) y=x² − 2
c) y=x² − 4
d) y=x² + 2

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

O gráfico apresentado é de uma função do tipo quadrática, e a forma geral dessa função é:

y = ax² + bx + c

Passos para identificar a função correta:

Observando o vértice:

O vértice está em (0, -4). Isso indica que o coeficiente c da função é -4, pois o valor mínimo ocorre em y = -4.

Analisando as raízes (x-interceptos):

As raízes são x = -2 e x = 2, indicando que a parábola corta o eixo x nesses pontos.

Substituindo as informações nas opções:

Apenas a opção c: y = x² – 4 satisfaz as condições do gráfico:

O vértice em (0, -4);

As raízes em x = -2 e x = 2.

Resposta final:

c) y = x² – 4

Gostou dessa questão? Que tal desafiar ainda mais seus conhecimentos? Clique aqui e resolva outra questão matemática preparada especialmente para você! 📚✨

[/toggle]

🟢Mapas Mentais de Matemática para Concurso

👉Entre no nosso canal do WhatsApp

📘 Todas as fórmulas de matemática em um só lugar! Baixe agora nosso eBook gratuito

Pronto para mergulhar em mais desafios matemáticos? 🚀 Explore nossa categoria completa com diversas questões matemática para testar e aprimorar seus conhecimentos! Clique aqui e comece agora! 📘✔️”