Na probabilidade, dizemos que três ou mais eventos A, B, C de um espaço amostral S são independentes se a ocorrência de qualquer combinação desses eventos não influencia as probabilidades dos demais. Isso é especialmente útil em experimentos em que os resultados de diferentes etapas ou ações não dependem entre si.

Definição de Independência de Três Eventos
Três eventos A,B,CA, B, C são independentes se:
- P(A∩B) = P(A)⋅P(B)
- P(A∩C) = P(A)⋅P(C)
- P(B∩C) = P(B)⋅P(C)
- P(A∩B∩C) = P(A)⋅P(B)⋅P(C)
Generalizando:
Para n eventos A1, A2, …, An, eles são independentes se, para qualquer subconjunto de eventos, a probabilidade da interseção for igual ao produto das probabilidades individuais.
Por exemplo:
P(A1 ∩ A2 ∩ … ∩ An) = P(A1)⋅P(A2)⋅…⋅P(An)
Exemplo 1: Lançamento de Moeda 10 Vezes
Problema:
Uma moeda é lançada 10 vezes. Qual é a probabilidade de obter cara em todos os 10 lançamentos?
Solução:
Definir os eventos:
- A1: Cara no 1º lançamento.
- A2: Cara no 2º lançamento.
- …
- A10: Cara no 10º lançamento.
Cada lançamento é independente dos demais, e a probabilidade de cara em qualquer lançamento é:
P(Ai) = 1/2, ∀i∈{1, 2, …, 10}
Cálculo:
A probabilidade de obter cara nos 10 lançamentos é:
P(A1 ∩ A2 ∩ … ∩ A10) = P(A1)⋅P(A2)⋅…⋅P(A10)
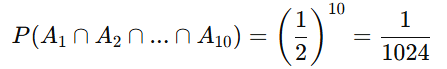
Interpretação:
A probabilidade de obter cara em todos os 10 lançamentos é 1/1024, ou aproximadamente 0,097%.
Exemplo 2: Lançamento de um Dado 5 Vezes
Problema:
Um dado é lançado 5 vezes. Qual é a probabilidade de que a face “2” apareça pelo menos uma vez?
Solução:
Definir os eventos:
- A1: Não ocorre “2” no 1º lançamento.
- A2: Não ocorre “2” no 2º lançamento.
- …
- A5: Não ocorre “2” no 5º lançamento.
A probabilidade de não ocorrer “2” em um único lançamento é:
P(Ai) = 5/6, ∀i ∈ {1, 2, …, 5}
Cálculo da probabilidade de não ocorrer “2” nos 5 lançamentos:
P(A1 ∩ A2 ∩ … ∩ A5) = P(A1)⋅P(A2)⋅…⋅P(A5)
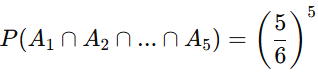
Cálculo da probabilidade de ocorrer “2” pelo menos uma vez:
A probabilidade de ocorrer “2” pelo menos uma vez é o complemento da probabilidade de não ocorrer “2” nenhuma vez:
P(ocorrer “2” pelo menos uma vez) = 1 − P(A1 ∩ A2 ∩ … ∩ A5)

Cálculo numérico:
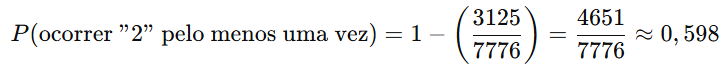
Interpretação:
A probabilidade de que a face “2” apareça pelo menos uma vez em 5 lançamentos é aproximadamente 59,8%.
Resumo de Propriedades Importantes
- Eventos independentes: A ocorrência de um evento não afeta a probabilidade dos outros.
- Para calcular P(A1∩A2∩…∩An), basta multiplicar as probabilidades individuais, desde que os eventos sejam independentes.
- A probabilidade de eventos complementares pode ser calculada usando
P(AC) = 1 − P(A)
Conclusão
A independência de três ou mais eventos na probabilidade é uma extensão do conceito básico de independência entre dois eventos. Esse princípio é aplicado em experimentos onde os eventos não afetam uns aos outros, como lançamentos de moedas ou dados. Dominar esse conceito é essencial para resolver problemas de probabilidade de forma eficiente e precisa.
Entenda também a Lei Binomial da Probabilidade que é uma ferramenta essencial para calcular probabilidades em experimentos que seguem os princípios dos ensaios de Bernoulli.

























