Introdução
As inequações exponenciais são expressões fundamentais na matemática, caracterizadas por desigualdades em que a variável desconhecida aparece no expoente. Resolver esse tipo de inequação é crucial para compreender diversos problemas em áreas como economia, física e biologia. Neste artigo, vamos aprofundar o conceito de inequações exponenciais, apresentar métodos de resolução e explorar exemplos práticos, oferecendo uma abordagem didática e completa para facilitar o entendimento do tema.
Definição de Inequação Exponencial
Uma inequação exponencial é uma desigualdade que envolve uma função exponencial. A forma geral de uma inequação exponencial pode ser expressa como:
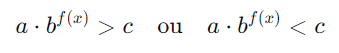
nde:
- a e c são constantes,
- b é a base da exponencial, um número positivo diferente de 1,
- f(x) é uma função de x, onde x é a variável desconhecida.
Exemplos de Inequações Exponenciais:
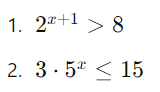
Propriedades das Inequações Exponenciais
As inequações exponenciais seguem algumas propriedades importantes, que dependem da base bbb:
- Base Maior que 1 (b>1):
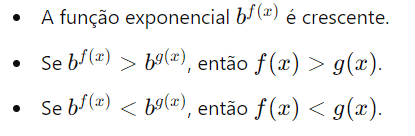
- Base entre 0 e 1 (0<b<1):

Essas propriedades são cruciais para determinar como resolver as inequações exponenciais.
Métodos de Resolução de Inequações Exponenciais
Existem diferentes métodos para resolver inequações exponenciais, dependendo da forma da inequação. Abaixo, exploramos os métodos mais comuns:
1. Comparação de Expoentes
Se as bases das expressões exponenciais são iguais, a inequação pode ser resolvida comparando os expoentes.
Exemplo:
Resolva
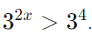
Solução:
Como as bases são iguais, podemos comparar os expoentes:
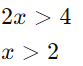
2. Reescrevendo as Bases
Quando as bases não são iguais, mas podem ser reescritas como potências da mesma base, podemos igualar os expoentes para resolver a inequação.
Exemplo:
Resolva
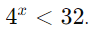
Solução:
Reescreva 4 e 32 como potências de 2:
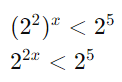
Agora, compare os expoentes:
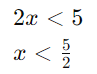
Exercício 1: Resolução de Inequação Exponencial com Base Maior que 1
Resolva a inequação
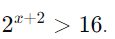
Solução:
- Reescreva 16 como uma potência de 2:
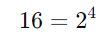
Então a inequação fica:
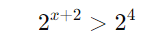
Como as bases são iguais, podemos igualar os expoentes:
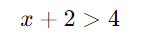
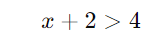
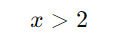
Resposta: A solução da inequação é x > 2.
Exercício 2: Resolução de Inequação Exponencial com Base Menor que 1
Problema: Resolva a inequação

Solução:
- Reescreva 2 como uma potência de 0,5:
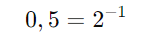
Assim:

Simplifique a potência:
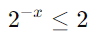

Resolva para x: Multiplique ambos os lados por -1 e inverta o sinal da desigualdade:
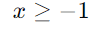
Resposta: A solução da inequação é x ≥ −1.