Introdução
As inequações logarítmicas são inequações que envolvem logaritmos e são fundamentais em diversas áreas da matemática aplicada, como economia, física e engenharia. Resolver uma inequação logarítmica implica encontrar o conjunto de valores que tornam a inequação verdadeira. Este artigo abordará a definição, os métodos de resolução, as propriedades e os exemplos de inequações logarítmicas, com o objetivo de fornecer uma compreensão clara e abrangente do tema.
O Que São Inequações Logarítmicas?
Uma inequação logarítmica é uma inequação que envolve uma ou mais expressões logarítmicas. A forma geral de uma inequação logarítmica é:
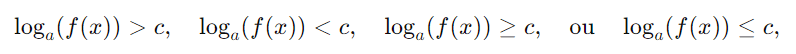
onde a é a base do logaritmo (com a>0 e a≠1), f(x) é uma função de x e c é uma constante real.
Condições de Existência
Antes de resolver uma inequação logarítmica, é crucial considerar as condições de existência. Para que loga(f(x)) esteja definida, a função f(x) deve ser positiva:

Essa condição garante que o argumento do logaritmo é válido, uma vez que o logaritmo de um número não positivo não está definido no conjunto dos números reais.
Métodos de Resolução de Inequações Logarítmicas
Para resolver uma inequação logarítmica, podemos seguir alguns passos gerais:
- Verificação das Condições de Existência:
- Primeiro, determine o domínio da função, garantindo que o argumento do logaritmo seja positivo.
- Aplicação das Propriedades dos Logaritmos:
- Use as propriedades dos logaritmos para simplificar a inequação, se necessário.
- Isolamento do Logaritmo:
- Procure isolar o logaritmo em um lado da inequação.
- Resolução da Inequação:
- Se a inequação estiver na forma loga(f(x))>c ou loga(f(x))<c, transforme a inequação em uma inequação exponencial e resolva-a.
- Se a base do logaritmo a>1, a inequação logarítmica mantém o sentido original da desigualdade.
- Se 0<a<1, o sentido da desigualdade se inverte.
- Interseção com as Condições de Existência:
- Interseccione o conjunto solução obtido com o domínio da função.

Propriedades Úteis na Resolução
- Propriedade do Produto: A propriedade do produto dos logaritmos estabelece que o logaritmo de um produto de dois números é igual à soma dos logaritmos desses números, ambos com a mesma base. Em outras palavras, para uma base a, a propriedade pode ser expressa como:
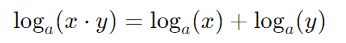
Essa propriedade é útil quando precisamos calcular logaritmos em uma base para a qual não temos uma tabela ou calculadora disponível.
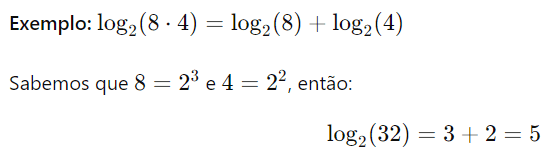
- Propriedade do Quociente: A propriedade do quociente dos logaritmos afirma que o logaritmo de um quociente entre dois números é igual à diferença entre os logaritmos desses números, ambos com a mesma base. Formalmente, para uma base aaa, essa propriedade é expressa como:
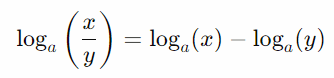
Essa propriedade é útil para simplificar expressões logarítmicas e resolver equações envolvendo divisões.
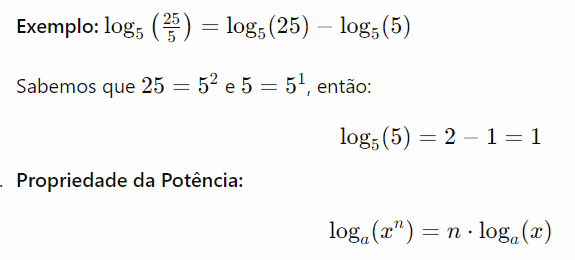
Propriedade da Potência: A propriedade da potência dos logaritmos estabelece que o logaritmo de um número elevado a um expoente é igual ao produto do expoente pelo logaritmo do número, ambos com a mesma base. Em termos formais, para uma base a, essa propriedade é dada por:
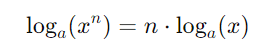
Essa propriedade facilita o processo de simplificação de expressões logarítmicas, especialmente quando lidamos com potências.
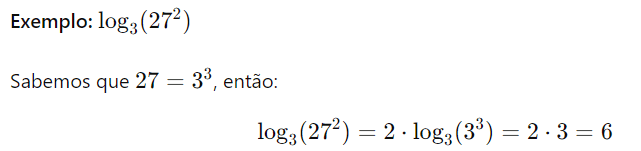
- Propriedade da Raiz: A propriedade da raiz dos logaritmos afirma que o logaritmo de uma raiz n-ésima de um número é igual ao logaritmo desse número dividido por n, ambos com a mesma base. Formalmente, para uma base a, essa propriedade pode ser expressa como:
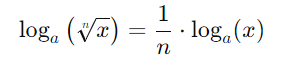
Essa propriedade é útil para simplificar expressões logarítmicas que envolvem raízes.
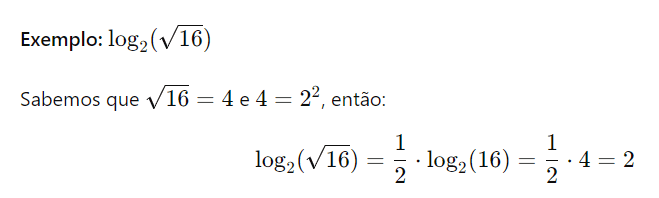
- Mudança de Base: A propriedade da mudança de base dos logaritmos permite calcular o logaritmo de um número em uma base diferente da original. Ela afirma que o logaritmo de um número x na base a pode ser expresso como a razão entre o logaritmo de x e o logaritmo de a em uma nova base b. Formalmente, a propriedade é dada por:
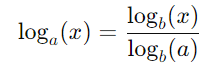
Essa propriedade é útil quando precisamos calcular logaritmos em uma base para a qual não temos uma tabela ou calculadora disponível.

Exemplos Resolvidos de Inequações Logarítmicas
Exemplo 1: Resolva a inequação log2(x−1)>3.

Exemplo 2: Resolva a inequação log0,5(2x+1) ≤ 2.

Exemplo 3: Resolva a inequação log3(x2−5x+6) ≥ 1.

Conclusão
As inequações logarítmicas são um tópico importante e aplicável em muitas áreas da matemática. Ao seguir um processo sistemático para resolver essas inequações, é possível encontrar soluções precisas e garantir que as condições de existência sejam atendidas. Com prática e compreensão das propriedades dos logaritmos, resolver inequações logarítmicas pode se tornar uma tarefa rotineira, ajudando a desbloquear uma ampla gama de aplicações práticas e teóricas.