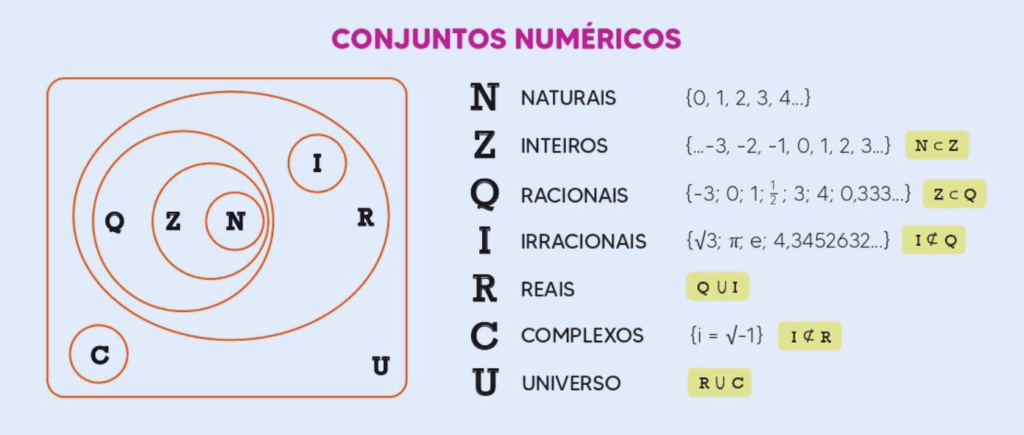
A matemática é uma disciplina que organiza e estrutura diferentes tipos de números em conjuntos. Esses conjuntos possuem propriedades e características distintas, sendo fundamentais para o entendimento de conceitos mais avançados. Neste artigo, exploraremos os principais conjuntos numéricos: os números naturais, inteiros, racionais, irracionais, reais e complexos. Cada um desses conjuntos desempenha um papel crucial na construção do conhecimento matemático.
1. Conjunto dos Números Naturais (ℕ)
O conjunto dos números naturais é o mais simples e intuitivo, formado pelos números que utilizamos para contar. Dependendo da convenção, os números naturais podem incluir ou não o zero.
- Definição: O conjunto dos números naturais inclui todos os números inteiros positivos e, em algumas definições, o zero.
- Notação: ℕ = {0, 1, 2, 3, 4, …}
- Exemplo: Se você tem três maçãs e ganha mais duas, você agora tem cinco maçãs. Este processo de contar utiliza números naturais.
Os números naturais são utilizados no dia a dia para quantificar objetos, pessoas, eventos e muito mais. Eles formam a base para a aritmética e são os primeiros números que aprendemos quando começamos a estudar matemática.
2. Conjunto dos Números Inteiros (ℤ)
À medida que avançamos na matemática, encontramos situações em que precisamos representar a ausência de quantidade ou o contrário de uma quantidade positiva, como a dívida ou a perda de algo. Para isso, utilizamos os números inteiros.
- Definição: O conjunto dos números inteiros inclui todos os números naturais, seus opostos (números negativos) e o zero.
- Notação: ℤ = {…, -3, -2, -1, 0, 1, 2, 3, …}
- Exemplo: Se uma pessoa deve três reais a alguém, pode-se representar isso como -3. Se pagar a dívida, a quantidade de dinheiro que possui agora será zero.
Os números inteiros expandem os naturais, permitindo a representação de perdas, dívidas e qualquer situação que envolva a subtração de uma quantidade maior do que a disponível.
3. Conjunto dos Números Racionais (ℚ)
Nem todos os números podem ser expressos como inteiros. Muitas vezes, lidamos com frações ou números que podem ser representados como a razão entre dois inteiros. Esses números formam o conjunto dos números racionais.
- Definição: Os números racionais são aqueles que podem ser expressos como uma fração p ÷ q, onde p e q são inteiros e q ≠ 0.
- Notação: ℚ = { p ÷ q\ p ∈ ℤ e ,q ∈ ℤ*}
- Exemplo: 1 / 2, 3 (que pode ser escrito como 3 / 1 , e -0,75 que é −3 / 4).
Os números racionais são úteis para representar quantidades que não podem ser expressas de forma inteira, como metade de um bolo, 0,25 litros de água, etc. Eles também são importantes para expressar razões e proporções.
4. Conjunto dos Números Irracionais
Enquanto os números racionais podem ser expressos como frações, há números que não podem ser escritos dessa forma. Esses números possuem expansões decimais infinitas e não periódicas.
- Definição: Os números irracionais são aqueles que não podem ser expressos como uma fração de dois inteiros. Suas representações decimais são infinitas e não periódicas.
- Exemplo: O número √2 é um número irracional porque sua representação decimal é 1,414213…, sem repetição. Outro exemplo famoso é o número π, que é aproximadamente 3,14159…
Os números irracionais são fundamentais em diversas áreas da matemática, especialmente em geometria e trigonometria. Eles surgem naturalmente em problemas que envolvem raízes quadradas e em relações envolvendo o círculo.
5. Conjunto dos Números Reais (ℝ)
O conjunto dos números reais é a união dos números racionais e irracionais. Ele abrange todos os números que podem ser representados em uma linha numérica contínua.
- Definição: Os números reais incluem todos os números racionais e irracionais.
- Notação: ℝ = {todos os números racionais e irracionais}
- Exemplo: Qualquer número que você possa imaginar em uma linha numérica, como 2, √2, -5, 0, π, 3,5, etc.
O conjunto dos números reais é essencialmente a totalidade da linha numérica. Ele permite a representação de qualquer quantidade contínua e é crucial na análise matemática e em muitas outras áreas da ciência.
6. Conjunto dos Números Complexos (ℂ)
À medida que a matemática evoluiu, descobriu-se que certas equações não tinham soluções no conjunto dos números reais. Para resolver essas equações, foi necessário criar um novo conjunto numérico: os números complexos.
- Definição: Os números complexos são expressos na forma a + bi, onde a e b são números reais e i é a unidade imaginária, tal que i2=−1.
- Notação: ℂ = {a + bi | a, b ∈ R}
- Exemplo: O número 3 + 4i é um número complexo, onde 3 é a parte real e 4i é a parte imaginária.
Os números complexos são fundamentais em diversas áreas da matemática, física, engenharia e ciências aplicadas. Eles permitem a resolução de equações que não têm solução entre os números reais e são usados em análises de ondas, circuitos elétricos e muitas outras aplicações.
Conclusão
Os conjuntos numéricos apresentados formam a base da matemática e são essenciais para a compreensão de fenômenos tanto no mundo abstrato quanto no mundo real. Desde a contagem simples com números naturais até a resolução de equações complexas, cada conjunto numérico desempenha um papel importante no desenvolvimento da matemática e de suas aplicações. Compreender a relação entre esses conjuntos e suas propriedades é fundamental para avançar em estudos matemáticos e em diversas disciplinas que utilizam a matemática como ferramenta.
Conjuntos Numéricos: Exercícios com Soluções Detalhadas