(CESPE / CEBRASPE 2005 – TRE-MT – Analista Judiciário)
Um aplicador pode investir R$ 60.000,00 por três períodos, tendo-lhe sido oferecida a seguinte alternativa: investir a juros simples de 20% por período ou a juros compostos de 18% por período. Nesse caso, irá preferir
A) a segunda aplicação, que lhe proporcionará maior rendimento.
B) a primeira aplicação, que lhe proporcionará maior rendimento.
C) qualquer uma das duas aplicações, por se equivalerem as remunerações.
D) a segunda aplicação, pois lhe permitirá sacar o rendimento a cada mês.
E) a primeira aplicação, pois lhe permitirá capitalizar o rendimento
Vamos comparar as duas opções de investimento para determinar qual delas proporcionará maior rendimento após três períodos, utilizando os conhecimentos da Matemática Financeira
Dados:
- Investimento inicial: R$ 60.000,00.
- Período: 3 períodos.
- Alternativa 1 (juros simples): 20% por período.
- Alternativa 2 (juros compostos): 18% por período.
Alternativa 1: Juros Simples de 20% por período.
A fórmula para calcular o montante com juros simples é:
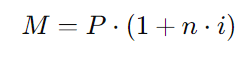
Onde:
- (M) é o montante,
- (P) é o capital inicial (R$ 60.000,00),
- (n) é o número de períodos (3),
- (i) é a taxa de juros por período (20% ou 0,20).
Substituindo os valores:
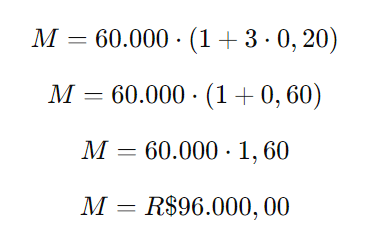
Alternativa 2: Juros Compostos de 18% por período.
A fórmula para calcular o montante com juros compostos é:
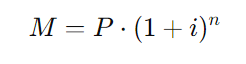
Substituindo os valores:
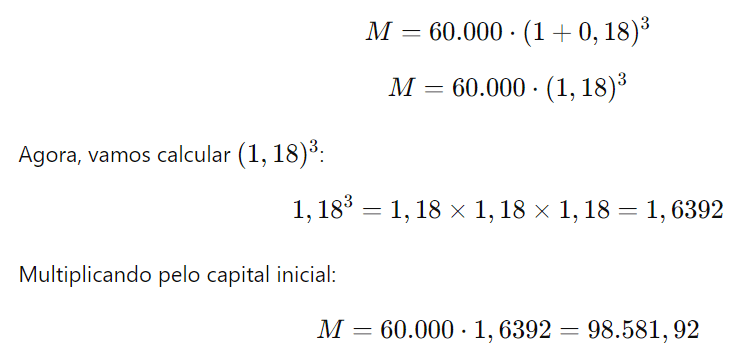
Comparação:
- Juros simples (20%): Montante = R$ 96.000,00.
- Juros compostos (18%): Montante = R$ 98.581,92.
A segunda aplicação (juros compostos) proporciona um montante maior.
Conclusão:
A Alternativa A está correta, pois o investidor preferirá a segunda aplicação, que lhe proporcionará maior rendimento.













