Confira a resolução detalhada de uma questão típica da banca VUNESP. Entenda o método e prepare-se para suas provas com confiança.
(Banca VUNESP – Nível Médio – 2023 – Estatística) A tabela apresentada a seguir contém informações sobre o número de filhos dos colaboradores de um setor de uma repartição pública:
As informações da tabela têm que ser representadas por um gráfico de setores, também conhecido como gráfico de pizza. Sendo assim, o ângulo central do maior setor tem que medir
A) 100º
B) 105º
C) 110º
D) 115º
E) 120º
Ver Solução
Estatística – Cálculo do Ângulo no Gráfico de Setores
Passo 1: Determinar o total de colaboradores
Somamos o número total de colaboradores:
14 + 24 + 20 + 10 + 4 = 72.
Passo 2: Identificar o maior grupo
O maior grupo é colaboradores com apenas 1 filho, com 24 pessoas.
Passo 3: Calcular o ângulo do setor correspondente
No gráfico de setores (gráfico de pizza), o ângulo de cada setor é proporcional à frequência do grupo em relação ao total. A fórmula é:
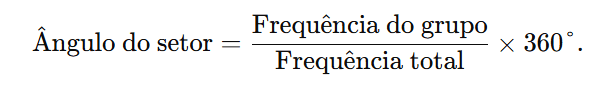
Substituímos os valores:
Ângulo do setor = 24/72 × 360°.
Simplificando:
Ângulo do setor = 1/3 × 360° = 120°.
Resposta
O ângulo central do maior setor é:
Alternativa correta: E) 120°.
Gostou desta questão? Confira outras questões resolvidas de Matemática VUNESP aqui.
👉Entre no nosso canal do WhatsApp
Questões Vunesp – Matemática PDF: Prepare-se com Qualidade
🟡Questões Resolvidas de Matemática em PDF da Banca VUNESP – Nível Fundamental
🔵Questões Resolvidas de Matemática em PDF da Banca VUNESP – Nível Médio
🟠Questões Resolvidas de Matemática em PDF da Banca VUNESP – Nível Superior
Raciocínio Lógico Lista em PDF Vunesp
🟣Raciocínio Lógico – Lista de Exercícios Vunesp (Nível Médio)
🟢Raciocínio Lógico – Lista de Exercícios Vunesp (Nível Superior)
🟢Mapas Mentais de Matemática para Concurso
