As matrizes são estruturas fundamentais na matemática, amplamente utilizadas em diversas áreas, como álgebra linear, física, economia e computação. Elas consistem em tabelas de números dispostos em linhas e colunas, e suas operações e propriedades formam a base para uma vasta gama de aplicações.
Definição de Matriz
Uma matriz é uma tabela de elementos dispostos em linhas e colunas, onde cada elemento pertence a um conjunto numérico específico, como os números reais ou complexos. Formalmente, uma matriz (A) de ordem (m x n) (lê-se “m por n”) é uma coleção de (m x n) elementos organizados em (m) linhas e (n) colunas:
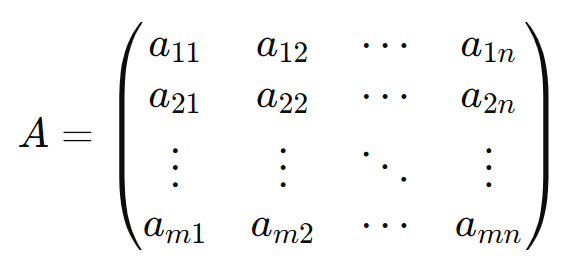
Cada elemento (aij) da matriz é denominado elemento da matriz e está localizado na i-ésima linha e j-ésima coluna.
Matriz Quadrada
Uma matriz quadrada é aquela em que o número de linhas é igual ao número de colunas, ou seja, uma matriz de ordem (n x n). Esse tipo de matriz é particularmente importante na álgebra linear, pois várias operações, como o cálculo de determinantes e de autovalores, são aplicáveis apenas a matrizes quadradas.
Exemplo:
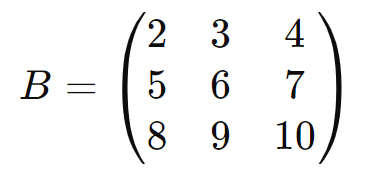
Neste exemplo, (B) é uma matriz quadrada de ordem 3.
Soma e Subtração de Matrizes
Duas matrizes (A) e (B) de mesma ordem (m x n) podem ser somadas ou subtraídas adicionando ou subtraindo os elementos correspondentes:
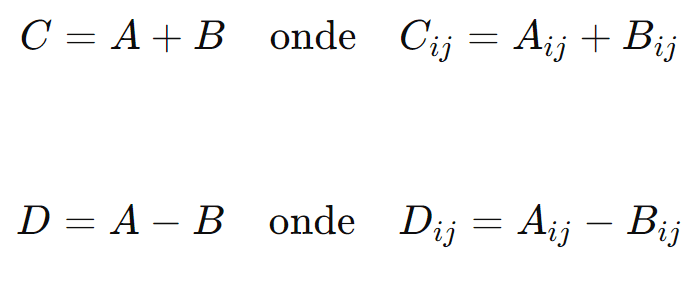
Exemplo:
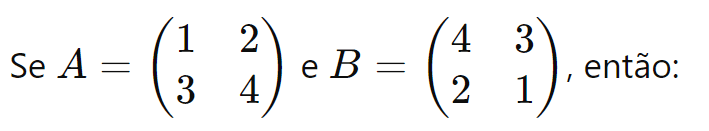
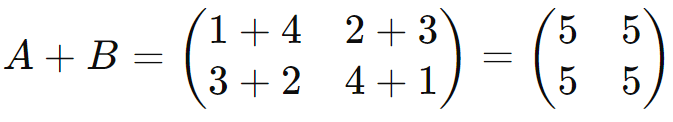
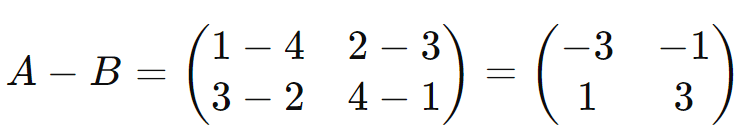
Produto de Matrizes
O produto entre duas matrizes (A) e (B) é possível se e somente se o número de colunas de (A) for igual ao número de linhas de (B). Se (A) é uma matriz de ordem (m x n) e (B) é uma matriz de ordem (n x p), o produto (C = A x B) resulta em uma matriz (C) de ordem (m x p), onde cada elemento (Cij) é dado por:
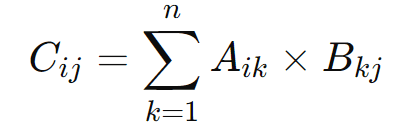
Exemplo:
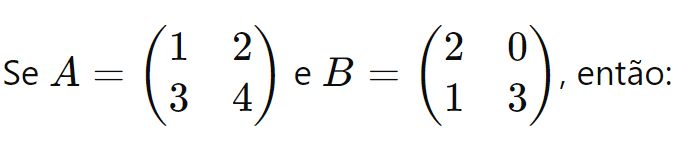
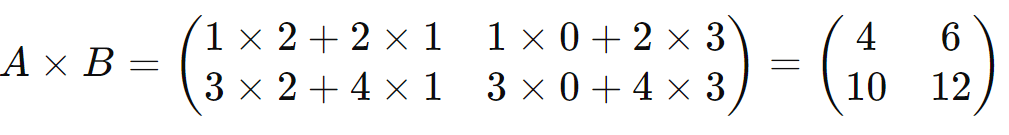
Produto de Matriz por um Número
O produto de uma matriz (A) por um número real (k) resulta em uma nova matriz (B), onde cada elemento (Bij) é o produto de (k) pelo elemento correspondente (Aij):
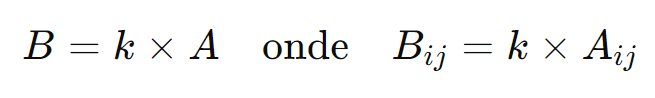
Exemplo:
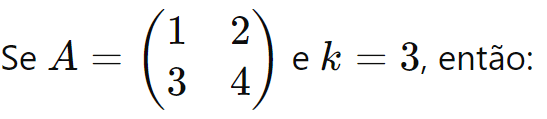
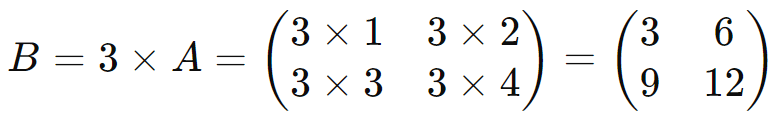
Matriz Transposta
A transposta de uma matriz (A), denotada por (A^T), é obtida trocando-se as linhas de (A) por colunas. Formalmente, se (A) é uma matriz (m x n), então (AT) é uma matriz (n x m), onde:
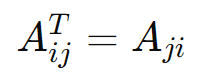
Exemplo:
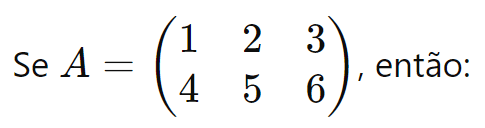
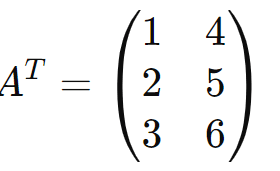
Matriz Inversa
A matriz inversa de uma matriz quadrada (A), denotada por (A-1), é a matriz que, quando multiplicada por (A), resulta na matriz identidade (I). A matriz (A) é invertível se e somente se seu determinante for diferente de zero.
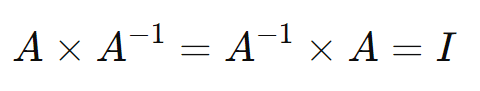
A inversa de uma matriz (2 x 2) pode ser calculada pela fórmula:
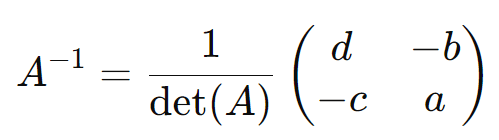
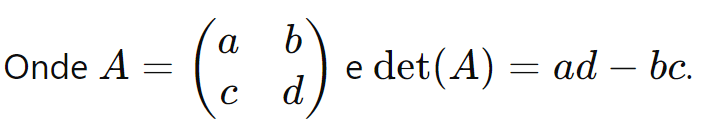
Exemplo:
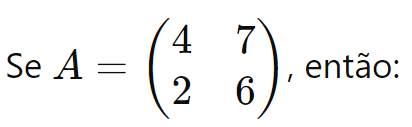
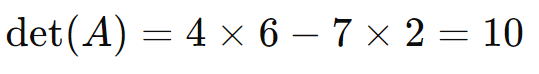
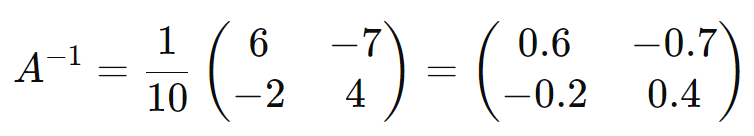
Matriz Oposta
A matriz oposta de uma matriz (A), denotada por (-A), é obtida multiplicando todos os elementos de (A) por (-1). Isso significa que a matriz oposta possui todos os elementos de (A) com sinais trocados.
Exemplo:
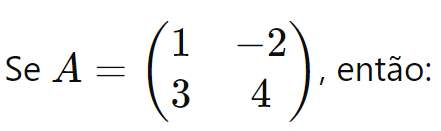
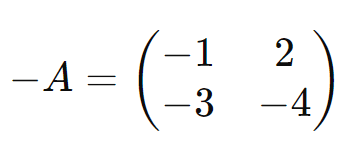
Conclusão
O estudo das matrizes é fundamental para a compreensão de conceitos avançados em matemática e outras disciplinas. Dominar as operações básicas, como soma, subtração, multiplicação e o cálculo da matriz inversa, é essencial para aplicações em sistemas lineares, transformações geométricas, álgebra abstrata e muitas outras áreas. As matrizes são ferramentas poderosas que permitem a modelagem e solução de problemas complexos de forma organizada e eficiente.
Leia também
Determinantes de Matrizes: Conceito, Exemplos e Propriedades
Sistemas Lineares Descomplicado: Guia Completo para Solução e Interpretação













