Os números naturais são a base da matemática e estão presentes no nosso dia a dia de várias maneiras. Eles começam a partir do zero (ou do um, dependendo da convenção) e seguem infinitamente na sequência dos números inteiros positivos. Entender os números naturais é fundamental para desenvolver habilidades matemáticas mais avançadas, e nada melhor do que praticar com exercícios para fixar o conhecimento.
Nesta lista de exercícios, você encontrará questões variadas sobre os números naturais, abrangendo operações básicas como adição, subtração, multiplicação e divisão. Cada exercício vem acompanhado de uma solução detalhada, explicando passo a passo como chegar à resposta correta. Seja você um estudante iniciando na matemática ou alguém revisando conceitos para um concurso, esta lista é uma excelente oportunidade para reforçar seu aprendizado e aprimorar suas habilidades.
Exercício 01 – Responda às perguntas.
a) 15 e XV representam quantidades diferentes?
b) 15 e XV são numerais diferentes?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
Exercício 02 – Sobre o número 478 194 235, responda:
a) Que algarismo ocupa a posição da centena de milhar?
b) Em que ordem está o algarismo 7?
c) Esse número é múltiplo de 2, de 3 ou de 5?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
Exercício 03 – Sobre os números naturais de 1 a 1 000,
responda:
a) Quantos têm o algarismo 5 na ordem das dezenas?
b) Quantos têm o algarismo 5 na ordem das unidades?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]


[/toggle]
Exercício 04 – Responda:
a) Quais são e como são chamados os números naturais múltiplos de 2?
b) Quais são os dez primeiros números naturais ímpares?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
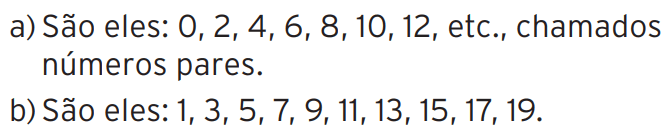
[/toggle]
Exercício 05 – Responda:
a) O que é um número natural primo?
b) Quais são os dez primeiros números naturais primos?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
Exercício 06 – Sobre o número 2 020, responda:
a) Sem considerar a ordem dos fatores, de quantos modos podemos obter o resultado 2 020 multiplicando dois números naturais?
b) E multiplicando três números naturais?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
Conjuntos Numéricos: Exercícios com Soluções Detalhadas
Exercício 07 – Considerando que dois números naturais são equivalentes se a soma dos divisores de um deles coincide com a soma dos divisores do outro, responda:
a) Os números 6 e 9 são equivalentes?
b) Os números 16 e 25 são equivalentes?
c) Existe algum número natural equivalente a 10? Qual?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
Exercício 08 – O que são dois números primos entre si? Dê um exemplo.
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
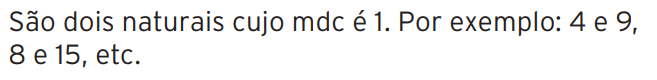
[/toggle]
Exercício 09 – Sabemos que um número natural é divisível por 6 quando é divisível por 2 e por 3. Isso ocorre porque 2 e 3 são números primos entre si e 6 5 2 3.
a) Como podemos saber se um número natural é divisível por 12, sem efetuar a divisão?
b) E por 15?
c) Dos números da lista abaixo quais são divisíveis por 12? E por 15?

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
Exercício 10 – Quantos são os múltiplos de 4 que possuem apenas dois algarismos?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
Exercício 11 – Considere a sucessão numérica abaixo.
7, 14, 21, 28, 35, 42, ….
Qual é o último número dessa sucessão que podemos representar com três algarismos?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
Exercício 12 – Na sequência de Fibonacci os dois primeiros números são 1 e 1. A partir daí, cada número é igual à soma dos dois anteriores:
1, 1, 2, 3, 5, 8, 13, 21, …
Qual é o primeiro número dessa sequência que se escreve com três algarismos?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
Exercício 13 – Na sequência numérica (2, 3,__ ,__ ,__ ,__ , …) a soma de três termos sucessivos é sempre igual a 10. Responda:
a) Quais são os números que estão representados por “__” na sequência?
b) Qual é o centésimo número dessa sequência?
c) Qual é a soma dos 100 primeiros números dessa sequência?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
Exercício 14 – Veja as duas sequências de números figurados a seguir.

Determine:
a) o próximo número de cada sequência;
b) o maior número com dois algarismos de cada sequência.
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
Exercício 15 – Decomponha os números abaixo em fatores primos:
a) 150
b) 1502
c) 500
d) 5002
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
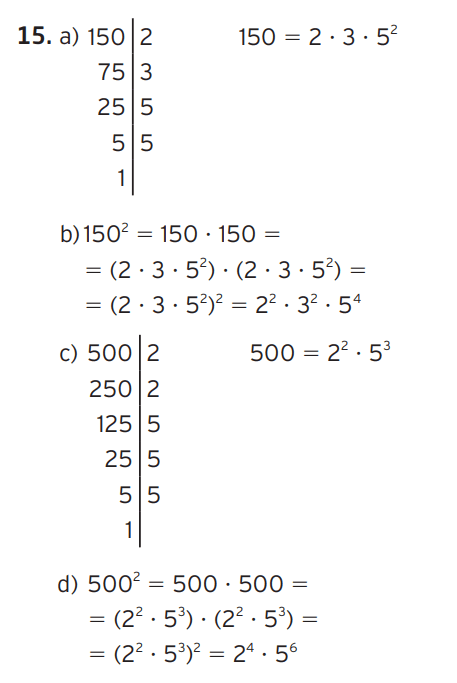
[/toggle]
Exercício 16 – Responda se a afirmação é verdadeira ou falsa:
“Sendo p um número natural maior que 1, na decomposição de p2 em fatores primos, todos os expoentes são números pares”.
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]
Exercício 17 – Dado o número p = 160, quantas vezes o número 2 aparece na de com posição em fatores primos de:
a) p
b) p2
c) 2 x p2
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]
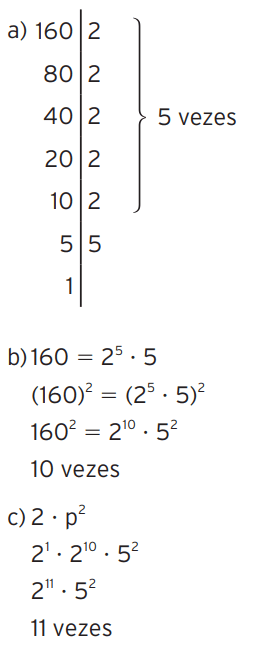
[/toggle]
Exercício 18 – Sendo p um número inteiro maior que 1, na decomposição em fatores primos do número p2 o expoente do fator primo 2 é par ou ímpar? E na decomposição do número 2p2?
[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]













