Potenciação e Radiciação 02: Lista de Exercício com Solução

A potenciação e a radiciação são operações que desempenham um papel central na matemática, permitindo simplificar expressões, resolver problemas e analisar propriedades de números e funções. A potenciação, que eleva um número a um determinado expoente, é essencial para cálculos rápidos e eficientes, enquanto a radiciação, o processo inverso, permite encontrar raízes e entender relações de proporção e escala.

Neste material, você encontrará uma série de exercícios cuidadosamente selecionados sobre potenciação e radiciação, com soluções detalhadas para cada questão. Cada passo foi explicado de maneira didática, com o objetivo de facilitar o entendimento e a aplicação prática desses conceitos. Aproveite para revisar, praticar e consolidar seus conhecimentos!

01 – Quantas sentenças abaixo são falsas?

• (7 + 3)² = 7² + 3²
• (7 + 3)² > 7² + 3²
• (7 × 3)² < 7² × 3²

a) nenhuma
b) uma
c) duas
d) três

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

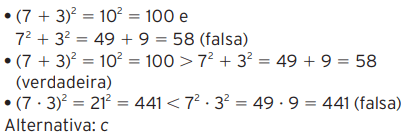
[/toggle]

02 – O dobro de 2²²² é:

a) 2²²³
b) 2⁴⁴⁴
c) 4²²²
d) 4⁴⁴⁴

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

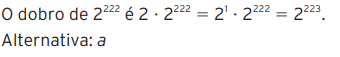
[/toggle]

03 – A décima parte de 10¹⁰ é:

a) 10¹
b) 1¹⁰
c) 9¹⁰
d) 10⁹

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

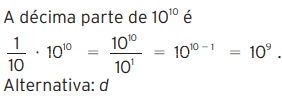
[/toggle]

04 – Quanto é 50% de 2¹⁰⁰?

a) 2⁹⁹
b) 2⁵⁰
c) 1
d) incalculável

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

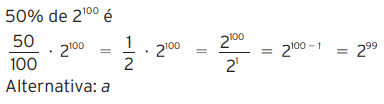
[/toggle]

05 – Cem milhões é o valor de:

a) (10²)³
b) 10^{2^3}
c) (10³)²
d) 10^{3^2}

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]

06 – Qual desses números é igual a 0,08?

a) (0,2)³
b) (0,2)³ ÷ 10
c) √0,64
d) √0,64 ÷ 10

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

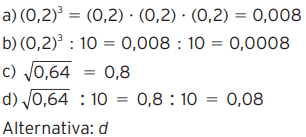
[/toggle]

07 – A raiz quadrada de (0,01)³ é igual a:

a) 0,1
b) 0,01
c) 0,001
d) 0,0001

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

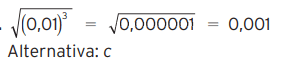
[/toggle]

Leia o enunciado a seguir para resolver os testes 8 e 9.

Na reta numérica abaixo o ponto O corresponde ao número 0 e o ponto A corresponde a um número racional quadrado perfeito.

08 – O quadrado do número representado por A está localizado:

a) à esquerda de O.
b) entre O e A.
c) entre A e +1.
d) à direita de +1.

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]

09 – A raiz quadrada aritmética do número representado por A está localizado:

a) à esquerda de O.
b) entre O e A.
c) entre A e +1.
d) à direita de +1.

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]

10 – Analise as igualdades abaixo e responda: quantas são verdadeiras?

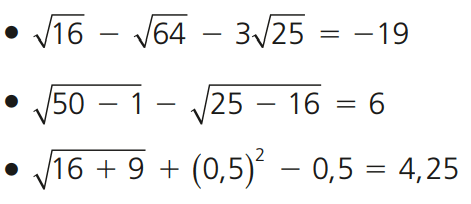
a) nenhuma
b) uma
c) duas
d) três

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

[/toggle]

11 – Abaixo está representado o conhecido “triângulo de Pascal”. Cada linha começa e termina com 1 e a soma de dois números consecutivos de uma linha resulta no número localizado na linha seguinte e na coluna abaixo do segundo número adicionado.

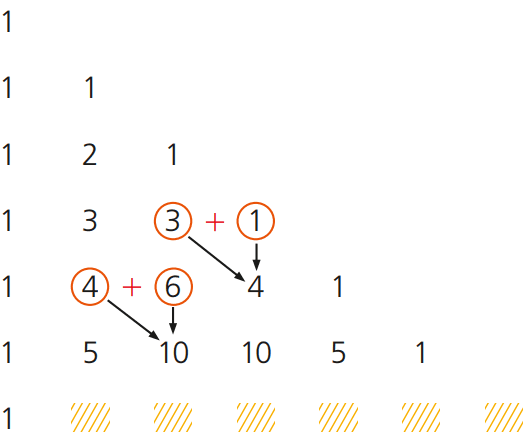
A soma dos números da última linha representada (onde estão os quadradinhos) é:

a) 2⁵
b) 2⁶
c) 5²
d) 6²

[toggle title=’Ver Solução’ ; toggle title_font_size=’20px’]

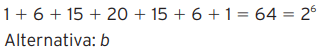
[/toggle]

Potenciação e Radiciação 01: Lista de Exercício com Solução