A potenciação é uma das operações matemáticas fundamentais que frequentemente encontramos tanto em situações cotidianas quanto em estudos avançados. Ela pode ser vista como uma forma de multiplicação repetida e desempenha um papel crucial em várias áreas da matemática básica, ciências, engenharia e tecnologia. Neste artigo, exploraremos todos os aspectos da potenciação de forma didática, abordando desde conceitos básicos até propriedades e aplicações mais complexas.
Definição de Potenciação
A potenciação é uma operação que envolve dois números: a base e o expoente. Ela é representada na forma:
an
onde:
- a é a base;
- n é o expoente;
- an é a potência.
A leitura dessa expressão é “a elevado à potência n” ou simplesmente “a elevado a n”.
Interpretação Básica
A potenciação é uma forma de multiplicação repetida. Se o expoente n é um número natural, a potenciação pode ser entendida da seguinte forma:
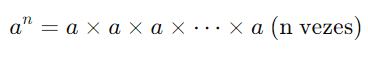
Por exemplo:
23=2×2×2=8
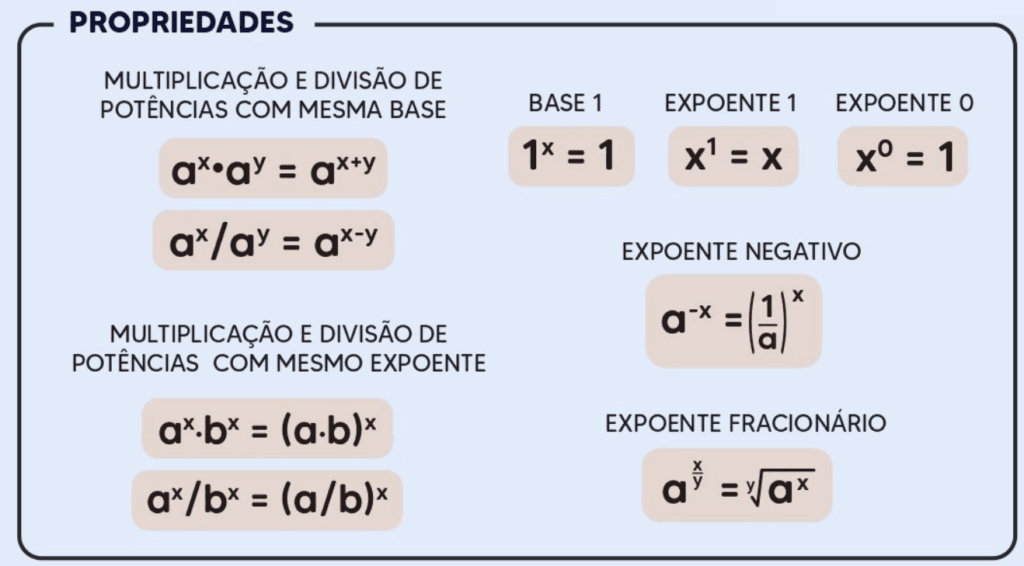
Propriedades da Potenciação
1. Propriedade do Produto de Potências de Mesma Base
Se você tem dois ou mais potências com a mesma base, pode multiplicá-las somando seus expoentes:
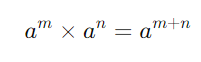
Exemplo:
23 × 22 = 23+2 = 25 = 32
2. Propriedade do Quociente de Potências de Mesma Base
Se você tem duas potências com a mesma base e as está dividindo, pode subtrair os expoentes:

Exemplo:
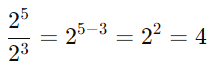
3. Potência de uma Potência
Quando elevamos uma potência a outra potência, multiplicamos os expoentes:

Exemplo:
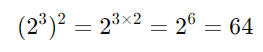
4. Potência de um Produto
Para multiplicar bases diferentes e elevá-las ao mesmo expoente, elevamos cada base ao expoente e multiplicamos os resultados:
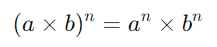
Exemplo:

Leia também: Produto Notável
5. Potência de um Quociente
Semelhante à propriedade anterior, quando dividimos bases diferentes e elevamos ao mesmo expoente, elevamos cada base ao expoente e, em seguida, dividimos:
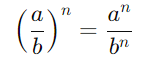
Exemplo:

Potências com Expoentes Especiais
1. Expoente Zero
Qualquer número diferente de zero elevado a zero é igual a 1:
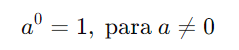
Exemplo:
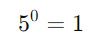
2. Expoente Um
Qualquer número elevado a 1 é igual ao próprio número:
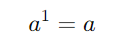
Exemplo:

3. Expoente Negativo
Um expoente negativo indica o inverso da base elevada ao expoente positivo:
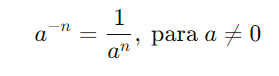
Exemplo:

Potenciação: Lista de Exercícios Resolvidos
Radiciação como Inversa da Potenciação
A radiciação é a operação inversa da potenciação. Ela responde à pergunta “Qual número elevado a n resulta em a?” A radiciação é expressa como:
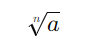
Por exemplo:
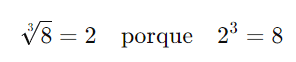
Radiciação: Lista de Exercícios Resolvido
Aplicações da Potenciação
A potenciação tem várias aplicações práticas em diferentes campos:
- Cálculo de juros compostos em finanças: o valor futuro VFVFVF de um investimento pode ser calculado usando a fórmula VF=P(1 + i)n, onde P é o principal, i é a taxa de juros e n é o número de períodos.
- Escalas logarítmicas em ciência: como na escala Richter para medir a magnitude de terremotos.
- Cálculos em física: como a lei do inverso do quadrado, onde a intensidade de uma força, como a gravidade ou a luz, diminui com o quadrado da distância.
Exercícios Práticos

Conclusão
A potenciação é uma operação matemática essencial com uma ampla gama de aplicações práticas e teóricas. Compreender suas propriedades e como aplicá-la em diferentes contextos é fundamental para o sucesso em várias disciplinas acadêmicas e na vida cotidiana. Esperamos que este artigo tenha fornecido uma visão abrangente e clara sobre o tema.
A Evolução da Potenciação: Da Antiguidade à Matemática Moderna
A história da potenciação remonta a tempos antigos, quando as primeiras civilizações começaram a explorar conceitos matemáticos básicos. O uso de multiplicação repetida, que é a base da potenciação, foi um dos primeiros passos para o desenvolvimento dessa operação.
Antiguidade
As primeiras noções de potenciação podem ser rastreadas até as civilizações babilônica e egípcia, que utilizavam métodos primitivos de multiplicação repetida para resolver problemas práticos, como o cálculo de áreas e volumes.
Matemática Grega
Os matemáticos gregos, como Euclides e Arquimedes, também exploraram conceitos relacionados à potenciação, embora de forma mais geométrica do que algébrica. O conceito de “potência” era frequentemente associado ao cálculo de áreas e volumes.
Idade Média
Durante a Idade Média, matemáticos islâmicos e europeus começaram a sistematizar as operações matemáticas. A notação moderna da potenciação começou a tomar forma, embora ainda não fosse amplamente utilizada.
Renascimento
No Renascimento, matemáticos como René Descartes e John Wallis contribuíram para a formalização da potenciação. Descartes, em particular, introduziu a notação de expoentes como os conhecemos hoje, usando potências para simplificar expressões matemáticas complexas.
Século XVII em diante
A potenciação se tornou uma operação central na matemática com o desenvolvimento do cálculo por Isaac Newton e Gottfried Wilhelm Leibniz. O uso de expoentes negativos e fracionários foi formalizado, expandindo o conceito de potenciação para além dos números inteiros positivos.
Era Moderna
Na era moderna, a potenciação continua a ser uma ferramenta fundamental em matemática e ciência, com aplicações que vão desde a computação e criptografia até a física quântica e a teoria dos números. Ela é essencial para o desenvolvimento de funções exponenciais e logarítmicas, que são usadas em uma vasta gama de disciplinas.
Em resumo, a potenciação evoluiu de uma prática rudimentar de multiplicação repetida para uma operação matemática formal e essencial, com ampla aplicação em diversas áreas do conhecimento.