Na Agência dos Correios de uma certa cidade trabalham 20 funcionários. Sabe-se que 12 desses funcionários jogam futebol, 8 jogam vôlei e 5 jogam futebol e vôlei. Escolhendo ao acaso um dos funcionários, qual a probabilidade dele não praticar nenhum desses esportes?
A) 12%
B) 5%
C) 25%
D) 50%
E) 75%
Ver Solução
Para resolver essa questão, vamos usar a fórmula do princípio da inclusão e exclusão.
Passo 1: Definir os conjuntos
- ( A ): conjunto de funcionários que jogam futebol.
- ( B ): conjunto de funcionários que jogam vôlei.
- ( |A| = 12 ) (12 funcionários jogam futebol).
- ( |B| = 8 ) (8 funcionários jogam vôlei).
- ( |A ∩ B| = 5 ) (5 funcionários jogam os dois esportes).
Passo 2: Calcular o total de funcionários que praticam pelo menos um dos esportes
A fórmula do princípio da inclusão e exclusão é:
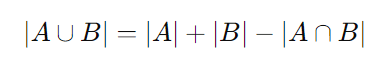
Substituindo os valores:
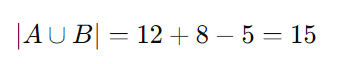
Então, 15 funcionários jogam futebol, vôlei ou ambos.
Passo 3: Calcular quantos funcionários não jogam nenhum dos esportes
O total de funcionários na agência é 20. Logo, o número de funcionários que não jogam nenhum dos esportes é:
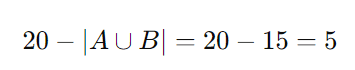
Passo 4: Calcular a probabilidade
A probabilidade de escolher um funcionário que não joga nenhum dos esportes é:
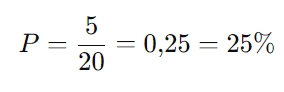
Resposta correta:
C) 25%
