(Fuvest-SP) Um marceneiro possui um pedaço de madeira no formato de um triângulo retângulo, cujos catetos medem 12 cm e 35 cm.

A partir desta peça, ele precisa extrair o maior quadrado possível, de tal forma que um dos ângulos retos do quadrado coincida com o ângulo reto do triângulo.

A medida do lado do quadrado desejado pelo marceneiro está mais próxima de:

• a) 8,0 cm
• b) 8,5 cm
• c) 9,0 cm
• d) 9,5 cm
• e) 10,0 cm

✅ Resolução passo a passo:

1. Observando a figura:

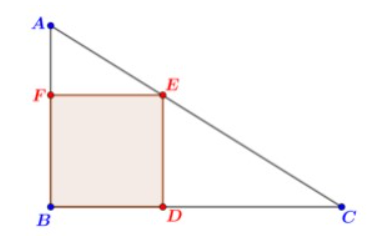
Figura: Ilustração da soldagem das barras com espessura de 18 mm.

O maior quadrado possível inscrito em um triângulo retângulo com um vértice coincidente ao ângulo reto tem uma fórmula direta:

\( x = \dfrac{ab}{a + b} \)

Onde \( a \) e \( b \) são os catetos. No caso:

\( a = 12, \quad b = 35 \)

2. Substituindo na fórmula:

\( x = \dfrac{12 \cdot 35}{12 + 35} = \dfrac{420}{47} \approx 8{,}936 \, \text{cm} \)

3. Arredondando para a alternativa mais próxima:

\( x \approx 9{,}0 \, \text{cm} \)

🔚 Conclusão: O maior quadrado que pode ser inscrito possui lado de aproximadamente 9,0 cm.

✅ Alternativa correta: c) 9,0 cm

📌 Indicações para aprofundar:

📖 Artigo recomendado:
Semelhança de Triângulos: Casos, Conceitos e Aplicações

🧠 Recursos para continuar aprendendo:

• 📘 Mapas Mentais de Matemática
• 📚 10 eBooks de Matemática para Baixar

📘 Lista completa com 10 questões resolvidas!

Veja agora uma seleção exclusiva de 10 questões resolvidas sobre Semelhança de Triângulos, Razão e Proporção com explicações visuais, passo a passo e botões interativos. Ideal para revisar conteúdos de geometria e se preparar para provas e concursos.