1 – (CESPE / CEBRASPE – 2024)
Se a média aritmética de 23 números inteiros não negativos diferentes é 167, então, nessas condições, o maior valor que um desses números pode assumir é
A) 3.841.
B) 3.610.
C) 3.588.
D) 3.379.
E) 3.335.
Ver Solução
Para resolver este problema, devemos usar o conceito de média aritmética e maximizar o valor de um dos números, sabendo que a média de 23 números inteiros diferentes não negativos é 167.
Passo a Passo:
- Calcular a soma total dos números:
A média aritmética de 23 números é dada por:
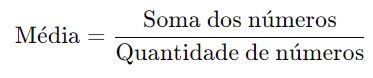
Substituindo os valores:
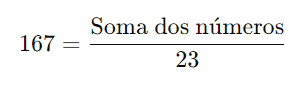
Multiplicando ambos os lados por 23:
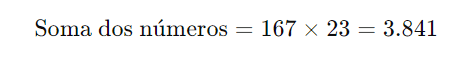
- Maximizar um dos números:
Para maximizar o valor de um dos números, vamos considerar que 22 números sejam os menores possíveis, que são 0, 1, 2, 3, …, 21. A soma desses 22 primeiros números é a soma dos 22 primeiros inteiros.
A soma dos primeiros (n) números inteiros é dada por:
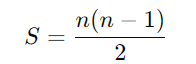
Para (n = 22):
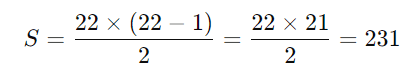
Agora, se a soma total é 3.841, e a soma dos 22 menores números é 231, o maior número possível (x) será:
x = 3.841 – 231 = 3.610
Conclusão:
O maior valor que um dos números pode assumir é 3.610.
Portanto, a resposta correta é:
B) 3.610.
2 – (CESPE / CEBRASPE – 2024)
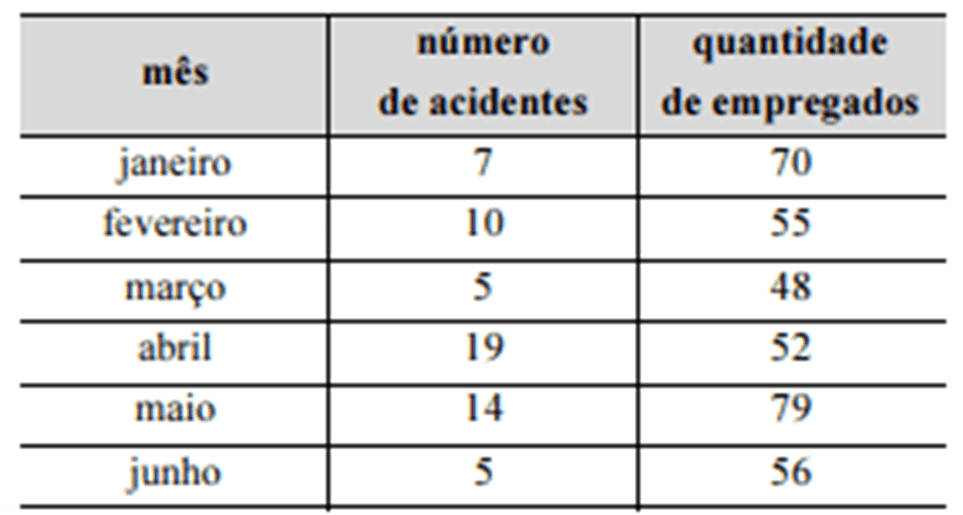
A tabela a seguir mostra dados sobre acidentes do trabalho compilados entre os meses de janeiro e junho por uma empresa de construção civil que opera em uma grande cidade.
Conforme os dados apresentados no texto 55A3, a6. média mensal de acidentes de trabalho foi igual a
A) 6.
B) 7.
C) 8.
D) 9.
E) 10.
Ver Solução
Para calcular a média mensal de acidentes de trabalho, somamos o número total de acidentes e dividimos pelo número de meses.
Passos para o cálculo:
- Somar o número total de acidentes:
Total de acidentes = 7 + 10 + 5 + 19 + 14 + 5 = 60 - Número de meses:
Existem 6 meses (de janeiro a junho). - Calcular a média mensal de acidentes:
Análise da Resposta:
A média mensal de acidentes de trabalho é 10.
Portanto, a resposta correta é:
E) 10.
3 – (CESPE / CEBRASPE – 2024)
bela a seguir mostra dados sobre acidentes do trabalho compilados entre os meses de janeiro e junho por uma empresa de construção civil que opera em uma grande cidade.
De acordo com os dados apresentados na tabela, a taxa média de acidentes de trabalho por empregado foi
A) superior a 0,16.
B) superior a 0,15 e inferior a 0,16.
C) superior a 0,14 e inferior a 0,15.
D) superior a 0,13 e inferior a 0,14.
E) inferior a 0,13.
Ver Solução
Para calcular a taxa média de acidentes de trabalho por empregado, precisamos dividir o número total de acidentes pelo número total de empregados ao longo dos meses apresentados.
Passos para o cálculo:
- Somar o número total de acidentes:
Total de acidentes = 7 + 10 + 5 + 19 + 14 + 5 = 60 - Somar a quantidade total de empregados:
Total de empregados = 70 + 55 + 48 + 52 + 79 + 56 = 360 - Calcular a taxa média de acidentes por empregado:
Análise da Resposta:
A taxa média de acidentes é aproximadamente 0,1667.
Comparando com as opções:
- A) superior a 0,16.
Essa é a opção correta, pois 0,1667 é superior a 0,16.
4 – (CESPE / CEBRASPE – 2024)
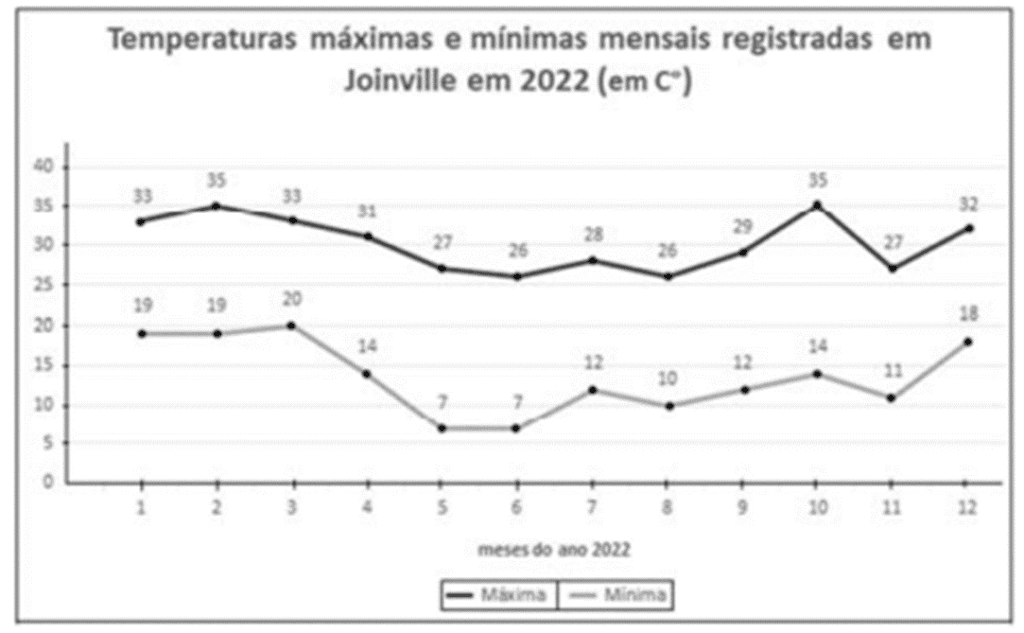
A maior diferença entre as temperaturas máximas e mínimas representadas no gráfico CB1A2 ocorreu no mês de
A) dezembro.
B) fevereiro.
C) maio.
D) agosto.
E) outubro.
Ver Solução
A maior diferença ocorre no mesmo de outubro 35 – 14 = 21C°
5 – (CESPE / CEBRASPE – 2024)
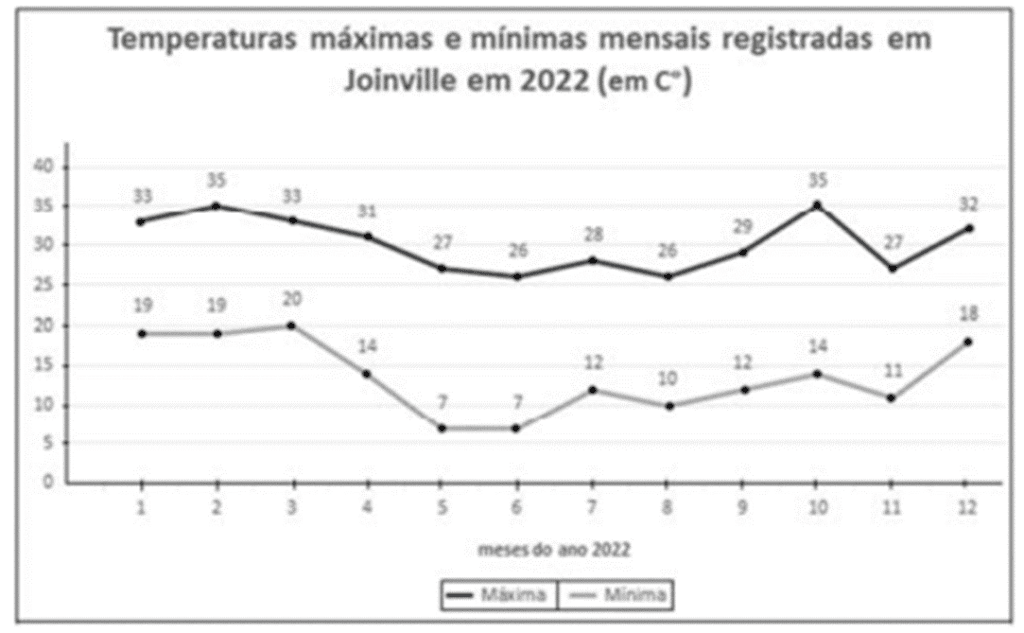
Com base no gráfico CB1A2, é correto afirmar que o valor da média das temperaturas máximas no primeiro semestre de 2022
A) foi inferior a 27,8 °C.
B) esteve entre 27,9 °C e 29,1 °C.
C) foi superior a 32,8 °C.
D) esteve entre 29,2 °C e 31 °C.
E) esteve entre 31,1 °C e 32,7 °C.
Ver Solução
Para determinar a média das temperaturas fornecidas, devemos somar todos os valores e depois dividir pelo número total de valores.
As temperaturas máximas do primeiro semestre são: 33 °C, 35 °C, 33 °C, 31 °C, 27 °C, 26 °C
Passo 1: Somar as temperaturas
33 + 35 + 33 + 31 + 27 + 26 = 185
Passo 2: Dividir pelo número de valores
O número de valores é 6, então calculamos a média:
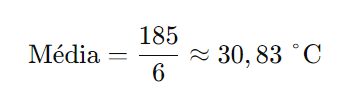
Resposta
Portanto, a média das temperaturas é aproximadamente 30,83 °C.
Resposta letra D) esteve entre 29,2 °C e 31 °C.
6 – (CESPE / CEBRASPE – 2024)
Em certa localidade, as temperaturas médias, nos meses de junho a novembro foram, respectivamente, de 21 °C, 21 °C, 22 °C, 23 °C, 25 °C e 26 °C.
Nessa situação hipotética, para que a temperatura média do semestre de julho a dezembro na referida localidade aumentasse 1 °C em relação à temperatura média do semestre de junho a novembro, a temperatura na referida localidade no mês de dezembro deveria ser de
A) 32 °C.
B) 23 °C.
C) 24 °C.
D) 27 °C.
E) 29 °C.
Ver Solução
Passo 1: Calcular a média das temperaturas de junho a novembro
As temperaturas médias de junho a novembro são 21°C, 21°C, 22°C, 23°C, 25°C e 26°C
Primeiro, somamos as temperaturas:
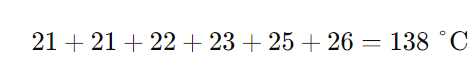
Agora, dividimos pelo número de meses (6 meses):
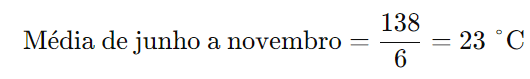
Passo 2: Determinar a média desejada para julho a dezembro
A média desejada para o semestre de julho a dezembro deve ser 1 °C maior do que a média do semestre de junho a novembro:
23 °C+1 °C=24 °C
Passo 3: Calcular a temperatura necessária em dezembro
Vamos somar as temperaturas dos meses de julho a novembro, que são 21°C, 22°C, 23°C, 25°C e 26°C
21 + 22 + 23 + 25 + 26 = 117 °C
Chamando a temperatura de dezembro de xxx, para que a média do semestre de julho a dezembro seja 24°C, precisamos que:
(21 + 22+23+25+26+x)/6=24 °C
Multiplicando ambos os lados por 6 para eliminar a fração:
117 + x = 144
Subtraindo 117 de ambos os lados:
x=427 °C
Portanto, a temperatura necessária para dezembro deve ser de 27°C para que a média do semestre seja 24°C.
A resposta correta é a Alternativa D: 27°C.
7 – (CESPE / CEBRASPE – 2024)
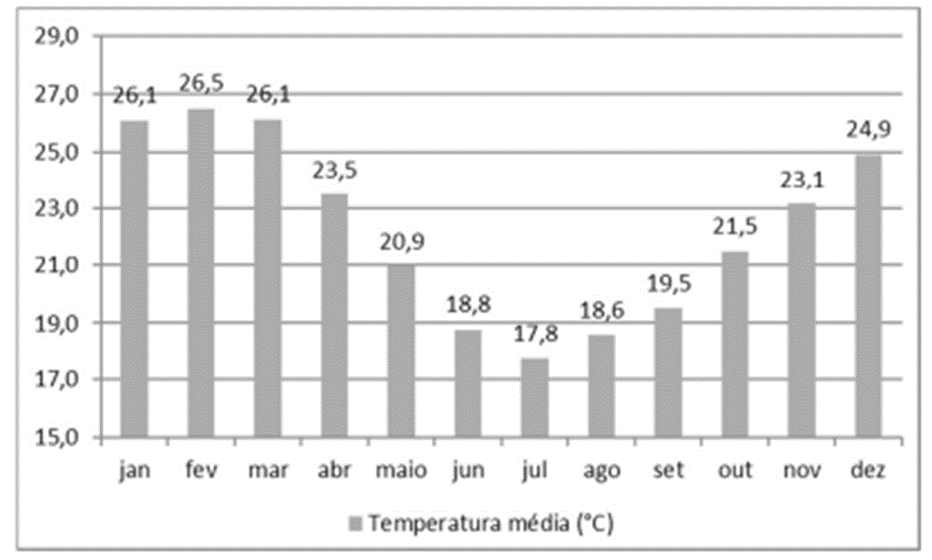
O gráfico precedente apresenta a temperatura média mensal em certa localidade.
Ainda a respeito do gráfico da figura CB2-A4, considere que, na localidade em questão, ao longo dos anos, o índice pluviométrico sempre varia de modo inverso à temperatura média mensal; isto é, um aumento gradual na temperatura média mensal causa diminuição do índice pluviométrico e vice-versa.
Com base nessa situação hipotética, o mês que terá o menor índice pluviométrico será o mês de
A) fevereiro.
B) abril.
C) julho.
D) dezembro.
E) outubro.
Ver Solução
Como o índice pluviométrico e inversamente a índice pluviométrico, quanto maior a temperatura menor o índice pluviométrico. Nesse caso, a resposta seria o mês de fevereiro. Letra A
8 – (CESPE / CEBRASPE – 2024)
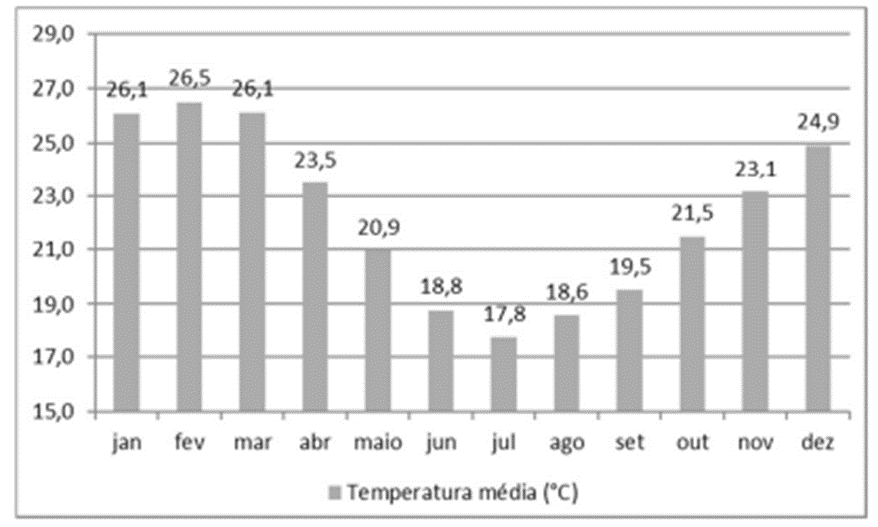
O gráfico precedente apresenta a temperatura média mensal em certa localidade.
Com base no gráfico da figura CB2-A4, assinale a opção que indica corretamente a média de temperatura dos 5 meses mais quentes do ano.
A) 24,62 °C
B) 26,1 °C
C) 24,9 °C
D) 25 °C
E) 25,42 °C
Ver Solução
Para calcular a média aritmética dos números 26,526,526,5, 26,126,126,1, 26,126,126,1, 24,924,924,9 e 23,523,523,5, siga os passos abaixo:
Passo 1: Somar todos os números
26,5 + 26,1 + 26,1 + 24,9 + 23,5 = 127,1
Passo 2: Dividir a soma pelo número de valores
Existem 5 valores na lista, então:
Média aritmética = 127,1/5 =25,42
Resposta
A média aritmética dos números é 25,42
8 – (CESPE / CEBRASPE – 2024)
Os números de homicídios, de 2011 a 2021, de determinado país estão representados na tabela a seguir. Com base nos dados apresentados no texto 2A4-II, julgue os itens a seguir.
I De 2020 a 2021, o número de homicídios diminuiu em aproximadamente 9,2%.
II No período de 2011 a 2021, o país apresentou uma média de homicídios por ano superior a 3.900.
III Se uma nova sequência de valores for criada, em que a primeira posição corresponda à média entre os anos 2011 e 2015, a segunda corresponda à média entre os anos 2012 e 2016, e assim por diante, o valor máximo dessa nova sequência será a média entre os anos 2015 e 2019.
Assinale a opção correta.
A) Apenas o item II está certo.
B)Apenas o item III está certo.
C) Apenas os itens I e II estão certos.
D) Apenas os itens I e III estão certos.
E) Todos os itens estão certos.
Ver Solução
9 – (CESPE / CEBRASPE – 2024)
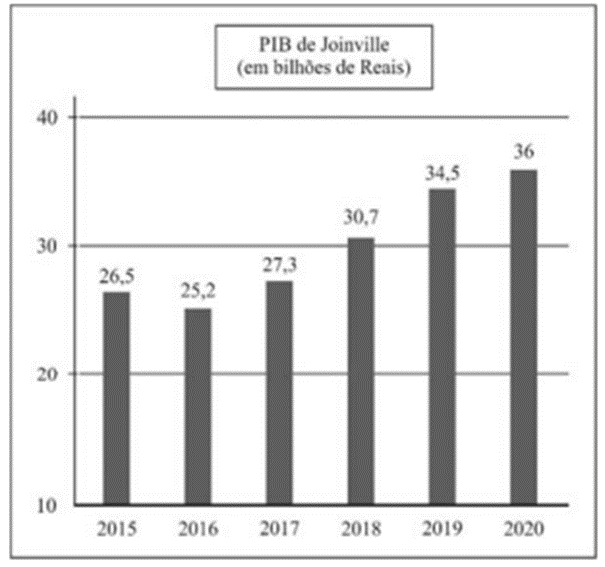
O gráfico a seguir apresenta a evolução do PIB da cidade de Joinville no período de 2015 a 2020.
A diferença, em bilhões de reais, entre a média e a mediana dos valores no gráfico 12A2 é
A) inferior a 0,97.
B) superior a 0,97 e inferior a 1,12.
C) superior a 1,12 e inferior a 1,17.
D) superior a 1,17 e inferior a 1,22.
E) superior a 1,22.
Ver Solução
Para encontrar a diferença entre a média e a mediana dos valores apresentados, siga estes passos:
- Organize os valores em ordem crescente:25,2; 26,5; 27,3; 30,7; 34,5; 36
- Calcule a média: A média é dada pela soma de todos os valores dividida pelo número de valores.
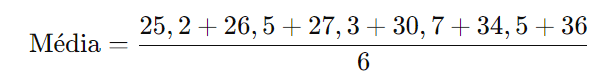
Agora, divida pelo número de valores (6):
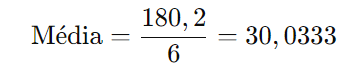
Calcule a mediana:
Como há um número par de valores (6), a mediana é a média dos dois valores centrais. Ordenando os valores, os dois valores centrais são 27,3 e 30,7.
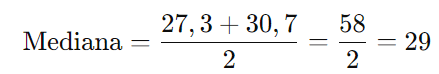
Calcule a diferença entre a média e a mediana:
Portanto, a diferença entre a média e a mediana é aproximadamente 1,0333 bilhões de reais.
A opção que mais se aproxima desse valor é:
B) superior a 0,97 e inferior a 1,12.
