10. Raciocínio Matemático
O raciocínio matemático é a habilidade de interpretar, analisar e resolver problemas matemáticos utilizando lógica, conceitos numéricos e operações matemáticas. Questões desse tipo são muito comuns em concursos públicos, pois avaliam a capacidade de aplicar conhecimentos básicos de matemática de forma lógica e eficiente.
10.1 Relações Entre Números
Números Pares e Ímpares:
- Números pares: Divisíveis por 2 (ex.: 2, 4, 6, …).
- Números ímpares: Não divisíveis por 2 (ex.: 1, 3, 5, …).
Identifique o próximo número par na sequência: 2, 4, 6, ….
Resposta: 8 (adicionando 2).
Divisibilidade:
Regras para determinar se um número é divisível por outro.
- Por 2: O número termina em 0, 2, 4, 6 ou 8.
- Por 3: A soma dos algarismos é divisível por 3.
- Por 5: O número termina em 0 ou 5.
O número 231 é divisível por 3?
Soma dos algarismos: 2 + 3 + 1 = 6, que é divisível por 3. Logo, 231 é divisível por 3.
👉Curso Gratuito de Raciocínio Lógico para Concursos
10.2 Problemas de Proporções e Frações
Proporções:
Uma proporção representa a igualdade entre duas razões.
Exemplo:
Se x/4 = 6/8, encontre o valor de x. Resolução:
Multiplicação cruzada:
8x = 4×6
8x = 24.
x = 3.
Frações:
- Soma e subtração: Quando os denominadores são iguais, somam-se os numeradores.Multiplicação: Multiplica-se numerador por numerador e denominador por denominador.Divisão: Multiplica-se pela inversa da segunda fração.
Resolva 3/4 + 5/4
Denominador comum: (3+5)/4 = 8/4 = 2
👉Entre no nosso canal do WhatsApp
10.3 Razões e Porcentagens
Razão:
É a comparação entre dois números ou grandezas. Representada na forma de fração. Exemplo:
A razão entre 8 e 12 é:
8/12 = 2/3
Porcentagem:
Representa uma parte de 100. A fórmula básica é:
Porcentagem = parte total × 100%
Exemplo:
Qual é 20% de 150?
20% = 20/100 = 0,2
0,2 × 150 = 30
10.4 Problemas com Sistema de Equações
Um sistema de equações é um conjunto de equações que envolvem as mesmas variáveis. Pode ser resolvido por:
- Método da substituição:
Isola-se uma variável em uma equação e substitui-se na outra. - Método da adição/elimininação:
Somam-se as equações para eliminar uma variável.
Exemplo:
Resolva o sistema:
x + y = 10 e x − y = 4
Resolução:
Somando as equações:
(x + y)+(x − y) = 10 + 4 ⟹ 2x = 14 ⟹ x = 7
Substituindo x = 7 na primeira equação:
7 + y = 10 ⟹ y = 3
Solução:
x = 7 e y = 3.
10.5 Sequências Numéricas
As sequências numéricas seguem padrões específicos, como:
Progressão Aritmética (PA): Aumenta ou diminui por um valor constante.
Exemplo: 2, 5, 8, 11, … (razão r = 3).
Progressão Geométrica (PG): Multiplica-se por um valor constante.
Exemplo: 2, 4, 8, 16, … (razão r = 2).
Exemplo:
Qual é o próximo termo da sequência 3, 6, 12, 24?
- Padrão: Multiplicação por 2.
- Próximo termo: 24×2 = 48
10.6 Problemas de Lógica Matemática
São problemas que envolvem raciocínio lógico aplicado a números.
Exemplo:
Uma pessoa tem 50 reais. Se ela gastar 40% do dinheiro, quanto restará?
Resolução:
- Valor gasto: 40% × 50 = 20
- Valor restante: 50 − 20 = 30
10.7 Exercícios Práticos
Exemplo 1: Uma torneira despeja 6 litros de água por minuto. Quantos litros serão despejados em 15 minutos?
Resolução:
- 6×15 = 90
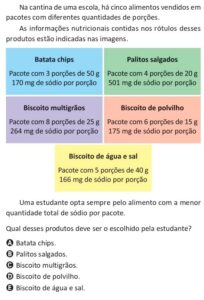
Exemplo 2: Em uma sala com 12 pessoas, cada uma cumprimenta todas as outras uma única vez. Quantos cumprimentos ocorrem?
Resolução:
Cada pessoa cumprimenta as outras: Combinação de 12 tomadas 2 a 2.
Fórmula:
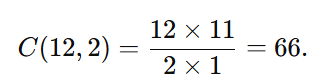
Total: 66 cumprimentos.
Conclusão
O raciocínio matemático é essencial para resolver problemas que envolvem relações numéricas, proporções, porcentagens, equações e sequências. Dominar os conceitos e praticar com exercícios variados é fundamental para desenvolver a agilidade e precisão necessárias em concursos públicos.
👉Curso Gratuito de Raciocínio Lógico para Concursos