O que são relações entre conjuntos?
Na teoria dos conjuntos, a relação entre conjuntos pode ser descrita de diferentes formas. Duas das relações mais importantes são “contém” e “está contido”, representadas pelos símbolos de inclusão ⊂ e ⊃.
Seja A e B dois conjuntos:
- Dizemos que A está contido em B (ou A ⊂ B) se todos os elementos de A pertencem a B.
- Dizemos que B contém A (ou B ⊃ A) se todos os elementos de A também pertencem a B.
Essas relações são essenciais para compreender a hierarquia e organização dos conjuntos matemáticos.
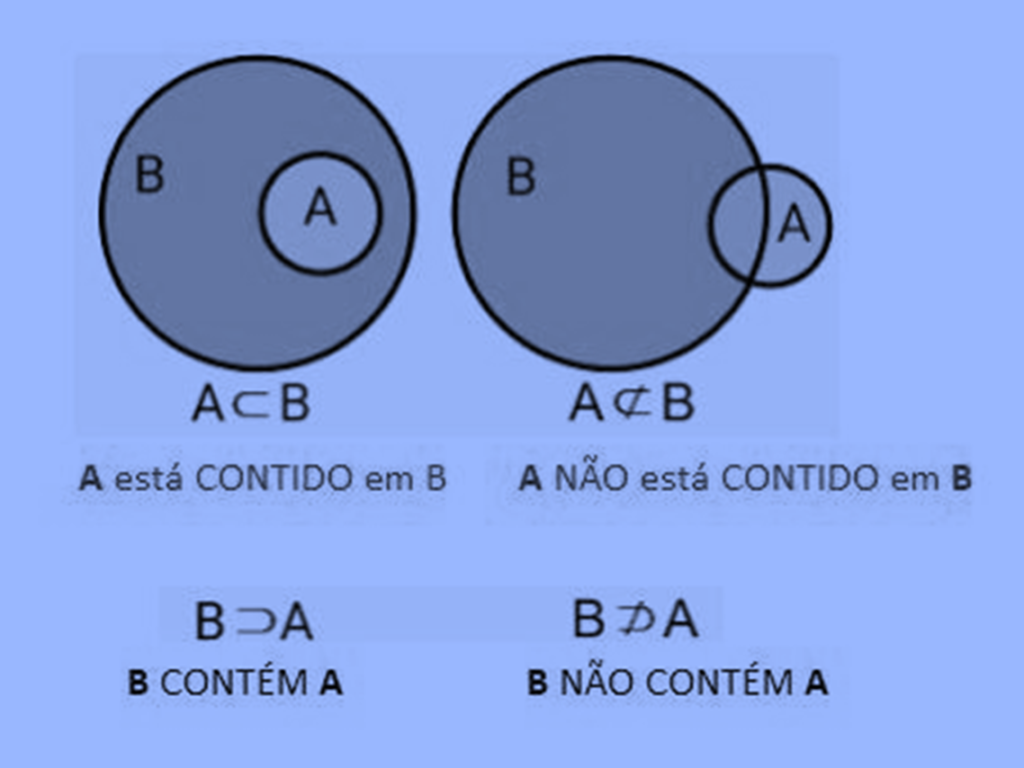
Diferença entre Contém e Está Contido
Para compreender melhor, vejamos um exemplo prático:
Seja A = {1, 2, 3} e B = {1, 2, 3, 4, 5}. Podemos afirmar que:
- A ⊂ B, pois todos os elementos de A pertencem a B.
- B ⊃ A, pois o conjunto B contém todos os elementos de A.
Dessa forma, a relação de inclusão é uma maneira de descrever a dependência entre conjuntos.
Exemplos Práticos
Exemplo 1: Conjunto dos números pares
Seja o conjunto dos números pares: P = {2, 4, 6, 8, 10, …} e o conjunto dos números naturais: N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, …}
Podemos dizer que:
- P ⊂ N (o conjunto dos números pares está contido nos números naturais).
- N ⊃ P (o conjunto dos números naturais contém o conjunto dos números pares).
Exemplo 2: Conjunto de vogais e alfabeto
Seja o conjunto das vogais: V = {a, e, i, o, u} e o conjunto do alfabeto: A = {a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z}
Podemos afirmar que:
- V ⊂ A (as vogais estão contidas no alfabeto).
- A ⊃ V (o alfabeto contém todas as vogais).
Exemplo 3: Conjunto de alunos
Seja o conjunto dos alunos de uma escola: E = {Ana, Bruno, Carlos, Daniela, Eduardo} e o conjunto dos alunos da turma A: T = {Ana, Carlos, Eduardo}
Temos que:
- T ⊂ E (a turma A está contida no conjunto dos alunos da escola).
- E ⊃ T (a escola contém a turma A).
Subconjunto Próprio e Subconjunto Improprio
- Subconjunto Próprio
Um subconjunto A é chamado de subconjunto próprio de B, se A está contido em B, mas A ≠ B, ou seja, B tem pelo menos um elemento a mais que A.
Exemplo: Se A = {1, 2} e B = {1, 2, 3}, então A ⊂ B, mas A ≠ B, logo, A é um subconjunto próprio de B.
- Subconjunto Impróprio
O subconjunto A é chamado de subconjunto impróprio de B, quando A é igual a B ou quando A é o conjunto vazio ∅.
Exemplo: Se A = {1, 2, 3} e B = {1, 2, 3}, então A = B e A ⊆ B, tornando-se um subconjunto impróprio.
Conjunto das Partes
O conjunto das partes de um conjunto A é o conjunto que contém todos os subconjuntos possíveis de A, incluindo o próprio A e o conjunto vazio.
Se A = {1, 2}, então o conjunto das partes de A é:
P(A) = {∅, {1}, {2}, {1, 2}}
Conclusão
A relação entre conjuntos é fundamental para organizar e classificar elementos dentro da matemática. As expressões “contém” e “está contido” ajudam a descrever essas relações e compreender melhor a estrutura dos conjuntos. A diferenciação entre subconjunto próprio e impróprio e o conceito de conjunto das partes são ferramentas essenciais para a compreensão mais aprofundada dessa área da matemática.
Com esses conceitos, é possível avançar para tópicos mais complexos, como operações entre conjuntos e diagramas de Venn, facilitando a aplicação em diversas áreas do conhecimento.