Os sistemas de equações lineares com duas incógnitas são um dos tópicos fundamentais em álgebra. Este artigo explora métodos práticos de resolução desses sistemas, como o método da substituição, o método da eliminação e o método da comparação, apresentando exemplos resolvidos passo a passo.
O que é um Sistema de Duas Equações com Duas Incógnitas?
Um sistema de duas equações com duas incógnitas consiste em duas equações lineares que compartilham as mesmas variáveis, geralmente chamadas de (x) e (y). A solução do sistema é um par ordenado (x, y) que satisfaz ambas as equações.
Exemplo de um Sistema Linear com Duas Equações:
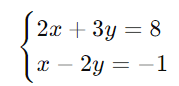
Métodos para Resolver Sistemas de Duas Equações com Duas Incógnitas
Existem três métodos principais para resolver sistemas de duas equações com duas incógnitas:
- Método da Substituição
- Método da Eliminação (ou Adição)
- Método da Comparação
1. Método da Substituição
O método da substituição consiste em resolver uma das equações para uma das variáveis e, em seguida, substituir essa expressão na outra equação.
Passos para o Método da Substituição:
- Escolha uma das equações e isole uma das variáveis.
- Substitua a expressão obtida na outra equação.
- Resolva a equação resultante para encontrar o valor da segunda variável.
- Substitua o valor encontrado na primeira equação para determinar o valor da outra variável.
Exemplo Resolvido:
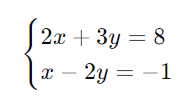
Passo 1: Isole (x) na segunda equação:
x = 2y – 1
Passo 2: Substitua (x) na primeira equação:
2(2y – 1) + 3y = 8
Simplifique a equação:

Passo 3: Substitua o valor de (y) na expressão para (x):
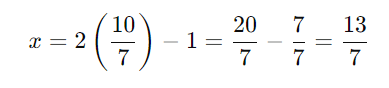
Logo, a solução do sistema é:
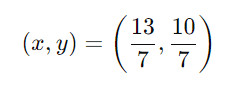
Veja também: Equação do Primeiro Grau
2. Método da Eliminação (ou Adição)
O método da eliminação envolve combinar as duas equações de maneira a eliminar uma das variáveis, permitindo resolver a equação restante para a outra variável.
Passos para o Método da Eliminação:
- Multiplique uma ou ambas as equações por um número para que os coeficientes de uma das variáveis sejam opostos.
- Some ou subtraia as equações para eliminar uma das variáveis.
- Resolva a equação resultante para encontrar o valor de uma variável.
- Substitua o valor encontrado em uma das equações originais para determinar o valor da outra variável.
Exemplo Resolvido:
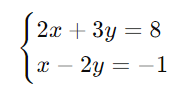
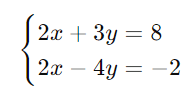
Passo 2: Subtraia a segunda equação da primeira:
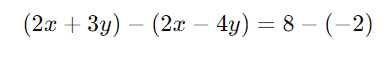
Simplifique a equação:
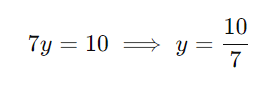
Passo 3: Substitua (y = 10/7) na segunda equação:
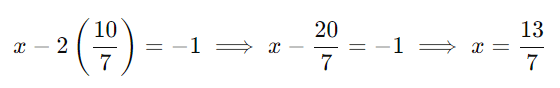
Assim, a solução do sistema é:
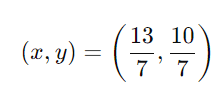
3. Método da Comparação
O método da comparação consiste em isolar a mesma variável nas duas equações e, em seguida, igualar as duas expressões obtidas para formar uma nova equação.
Passos para o Método da Comparação:
- Isole a mesma variável em ambas as equações.
- Iguale as duas expressões obtidas.
- Resolva a equação resultante para encontrar o valor de uma das variáveis.
- Substitua o valor encontrado em uma das equações originais para determinar o valor da outra variável.
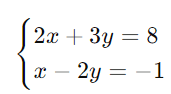
Passo 1: Isole (x) em ambas as equações:

Passo 2: Iguale as duas expressões para (x):
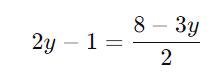
Multiplique todos os termos por 2 para eliminar o denominador:
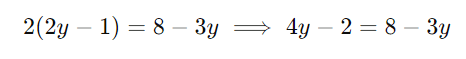
Passo 3: Resolva para (y):
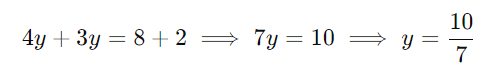
Passo 4: Substitua o valor de (y) em uma das expressões para (x):
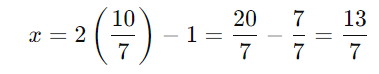
Logo, a solução do sistema é:
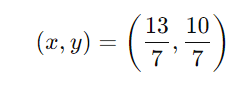
Exercícios Resolvidos
Exercício 1:
Resolva o sistema abaixo utilizando o método da substituição:
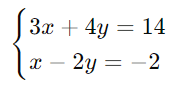
Solução:
Isole (x) na segunda equação:
x = 2y – 2
Substitua na primeira equação:
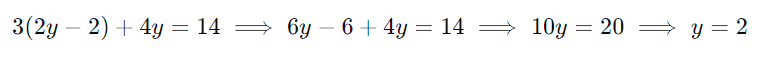
Substitua (y = 2) em (x = 2y – 2):
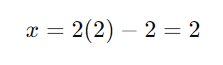
Solução: ((x, y) = (2, 2)).
Exercício 2:
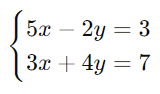
Solução:
Isole (x) na primeira equação:
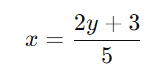
Isole (x) na segunda equação:
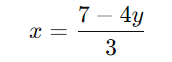
Iguale as duas expressões para (x):
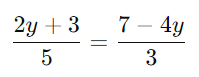
Multiplique todos os termos por 15 para eliminar os denominadores:
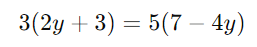
Simplifique e resolva para (y):
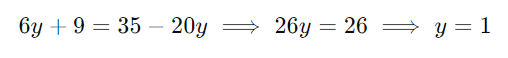
Substitua (y = 1) em uma das expressões para (x):
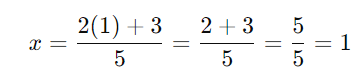
Logo, a solução do sistema é: (x, y)=(1, 1)
Conclusão
Os sistemas de duas equações com duas incógnitas podem ser resolvidos de várias maneiras na matemática. O método da substituição é eficaz quando uma das variáveis é fácil de isolar, o método da eliminação é útil quando é possível igualar coeficientes para cancelar variáveis, e o método da comparação é direto quando ambas as variáveis podem ser isoladas facilmente. A escolha do método depende da estrutura do sistema e da preferência de quem resolve o problema.
A prática dos três métodos ajuda a entender melhor as diferentes abordagens e a desenvolver a habilidade de escolher a melhor estratégia para cada situação.













