Sistemas Lineares Descomplicado: Guia Completo para Solução e Interpretação

Os sistemas lineares são conjuntos de equações lineares que compartilham um conjunto de variáveis. Resolver um sistema linear significa encontrar os valores das variáveis que satisfazem simultaneamente todas as equações do sistema. Eles são amplamente utilizados em diversas áreas da ciência, engenharia, economia, entre outras.

Neste artigo, exploraremos sistemas lineares com duas e três equações, discutindo métodos clássicos de solução, como substituição, soma, comparação, escalonamento e determinantes, além de como interpretar e classificar os resultados.

Sistemas Lineares com Duas Equações

Um sistema linear com duas equações pode ser representado da seguinte forma:

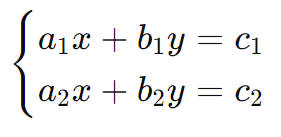
Onde x e y são as variáveis, e a₁, b₁, c₁, a₂, b₂ e c₂ são constantes. Existem três métodos principais para resolver tais sistemas: substituição, soma (ou eliminação) e comparação.

Método de Substituição

O método de substituição consiste em resolver uma das equações para uma variável e, em seguida, substituir essa expressão na outra equação.

Passos:

1. Isolar uma das variáveis em uma das equações.
2. Substituir essa expressão na outra equação.
3. Resolver a equação resultante para encontrar o valor da segunda variável.
4. Substituir o valor encontrado de volta na expressão isolada para encontrar o valor da primeira variável.

Exemplo:

Considere o sistema:

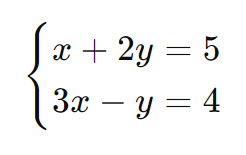
1. Isolamos x na primeira equação: x = 5 – 2y.
2. Substituímos x na segunda equação: 3(5 – 2y) – y = 4.
3. Resolvemos: 15 – 6y – y = 4 ⇒ -7y = -11 ⇒ y = 11/7.
4. Substituímos y em x = 5 – 2y ⇒ x = 5 – 2(11/7) = 24/7.

Portanto, a solução é x = 24/7 e y = 11/7.

Método da Soma (Eliminação)

No método da soma, somamos as equações de forma a eliminar uma das variáveis, permitindo resolver para a outra.

Passos:

1. Multiplicar as equações por constantes, se necessário, para que os coeficientes de uma das variáveis sejam opostos.
2. Somar as equações para eliminar essa variável.
3. Resolver a equação resultante.
4. Substituir o valor encontrado na equação original para encontrar a outra variável.

Exemplo:

Considere o sistema:

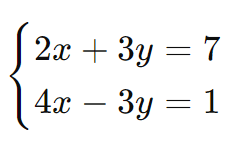
1. Somamos as equações: 2x + 3y + 4x – 3y = 7 + 1.
2. Isso resulta em: 6x = 8 ⇒ x = 4/3.
3. Substituímos x na primeira equação: 2.(4/3) + 3y = 7, o que resulta em y = 1/3.

Logo, a solução é x = 4/3 e y = 1/3.

Método da Comparação

O método da comparação envolve resolver ambas as equações para a mesma variável e, em seguida, igualar as duas expressões obtidas.

Passos:

1. Resolver ambas as equações para a mesma variável.
2. Igualar as duas expressões.
3. Resolver a equação resultante.
4. Substituir o valor encontrado em uma das equações originais para encontrar a outra variável.

Exemplo:

Dado o sistema:

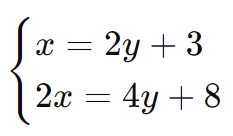
1. Resolver a primeira equação para x: x = 2y + 3.
2. Resolver a segunda para x: x = 2y + 4.
3. Igualar as duas expressões: 2y + 3 = 2y + 4, o que é uma contradição (não há solução).

Neste caso, o sistema é inconsistente e não possui solução.

Sistemas Lineares com Três Equações

Um sistema com três equações é representado por:

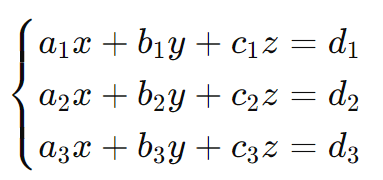
Esses sistemas podem ser resolvidos por escalonamento ou usando determinantes.

Cálculo por Escalonamento

O método do escalonamento envolve manipular as equações para transformar o sistema em uma forma triangular, permitindo resolver as variáveis por substituição retroativa.

Passos:

1. Usar operações elementares para eliminar uma variável de duas das equações.
2. Repetir o processo para obter uma equação com apenas uma variável.
3. Resolver a equação resultante e usar substituição retroativa para encontrar as outras variáveis.

Exemplo:

Considere o sistema:

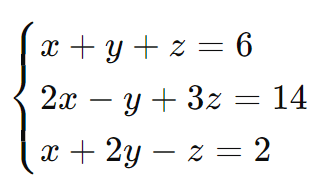
1. Subtrair a primeira equação da segunda e da terceira para eliminar x:

• (2x – y + 3z) – (x + y + z) = 8 resulta em x – 2y + 2z = 8.
• (x + 2y – z) – (x + y + z) = -4 resulta em y – 2z = -4.

1. Substituir y = 2z – 4 na equação resultante e resolver.

Agora temos um sistema reduzido:

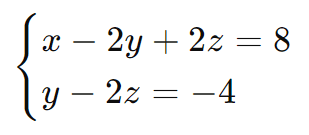
Isolamos y na segunda equação:

y − 2z = −4

y = 2z – 4

Substituímos y = 2z − 4 na primeira equação:

x − 2(2z − 4) + 2z = 8

Simplificando:

x−4z+8+2z=8

x−2z+8=8

x−2z=0

x=2z

Agora temos:

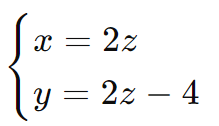
Substituímos x = 2z e y = 2z−4y na primeira equação:

(2z) + (2z − 4) + z=6

Cálculo por Determinantes

O método de Cramer, que utiliza determinantes, é uma técnica algébrica eficiente para resolver sistemas lineares.

Passos:

1. Calcular o determinante da matriz dos coeficientes.
2. Calcular os determinantes das matrizes obtidas ao substituir cada coluna pela coluna dos termos independentes.
3. Resolver as variáveis usando as fórmulas:

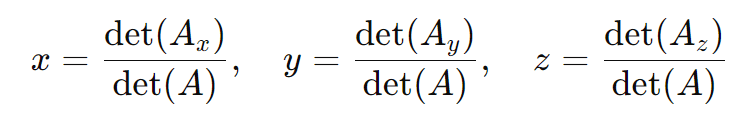
Exemplo:

Para um sistema com matriz de coeficientes:

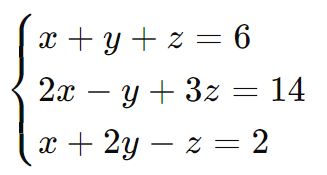
Para resolver este sistema usando determinantes, aplicaremos o Método de Cramer. Primeiro, montaremos a matriz dos coeficientes e as matrizes auxiliares obtidas substituindo uma coluna pela coluna dos termos independentes.

A matriz dos coeficientes A é:

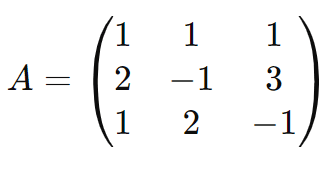
Calculamos o determinante de A, det(A)

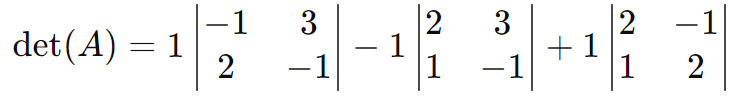
Calculamos os determinantes 2×2:

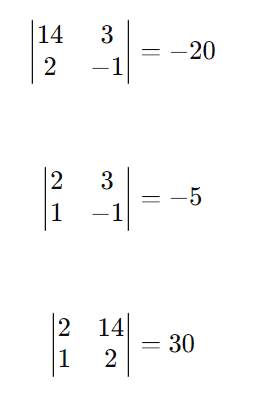
Então

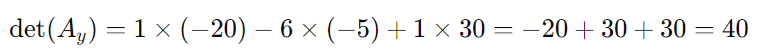
Calculamos det(Az)

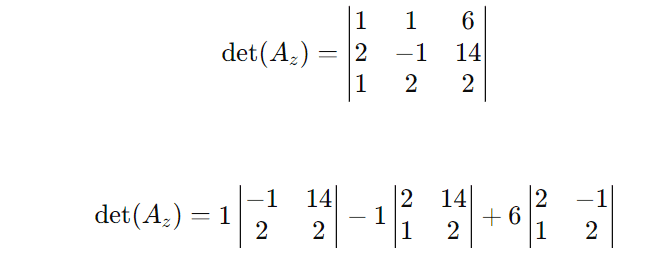
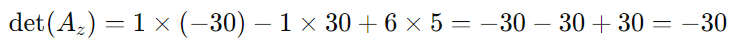
Repetindo o processo para Ax e Ay, temos

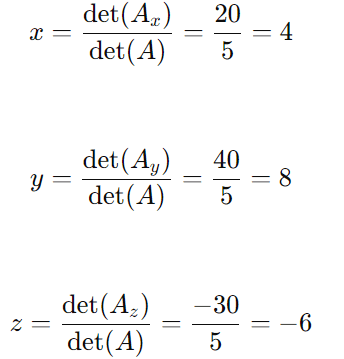
Interpretando os Resultados dos Determinantes

A análise dos determinantes revela a natureza do sistema:

1. Sistema Determinado: Quando o determinante da matriz dos coeficientes det(A) é diferente de zero, o sistema tem uma única solução.
2. Sistema Indeterminado: Se det(A) = 0 e os determinantes substituídos também são zero, o sistema possui infinitas soluções.
3. Sistema Impossível: Se det(A) = 0 e pelo menos um dos determinantes substituídos não é zero, o sistema não tem solução.

Classificação do Sistema Linear

Os sistemas lineares podem ser classificados de acordo com o número de soluções:

1. Sistema Compatível Determinado (SCD): Possui uma única solução.
2. Sistema Compatível Indeterminado (SCI): Possui infinitas soluções.
3. Sistema Incompatível (SI): Não possui solução.

Conclusão

Sistemas lineares são ferramentas essenciais na matemática, com aplicações significativas em diversas áreas como engenharia, economia e ciências sociais. Compreender os diferentes métodos para resolver esses sistemas permite não apenas encontrar soluções precisas, mas também interpretar e classificar os resultados de forma eficaz.

Para sistemas com duas equações, os métodos de substituição, soma (ou eliminação) e comparação são úteis para encontrar as soluções. Cada método oferece uma abordagem única, mas todos visam encontrar os valores das variáveis que satisfazem simultaneamente as equações.

Para sistemas com três equações, o método de escalonamento simplifica o sistema até que as variáveis possam ser resolvidas por substituição retroativa. Alternativamente, o método de Cramer usa determinantes para resolver o sistema de maneira algébrica. Ambos os métodos são valiosos, dependendo do contexto e da complexidade do sistema.

Interpretar os resultados dos determinantes fornece uma visão clara sobre a natureza do sistema linear. Através da análise do determinante da matriz dos coeficientes e dos determinantes substituídos, é possível determinar se o sistema tem uma solução única, infinitas soluções ou nenhuma solução.

A classificação dos sistemas lineares ajuda a categorizar a natureza do sistema e a direcionar a abordagem correta para a solução. Com um sistema determinado, você obtém uma solução única; com um sistema indeterminado, infinitas soluções; e com um sistema impossível, nenhuma solução.

Com esses conhecimentos, você estará bem equipado para resolver e analisar sistemas lineares em diferentes contextos, tornando-se mais proficiente na aplicação de métodos matemáticos para resolver problemas reais.

Leia também

Matriz: o que é, tipos, operações, exercícios

Determinantes de Matrizes: Conceito, Exemplos e Propriedades

Entendendo o Binômio de Newton