Teorema de Tales
A proporcionalidade pode ser utilizada em diversos casos do nosso cotidiano. Nesse sentido, o teorema de Tales, que será apresentado a seguir, trata da relação entre os segmentos de reta determinados por um feixe de retas paralelas e duas retas transversais.
Por meio desse teorema, podemos realizar cálculos para determinar, por exemplo, distâncias que não podem ser medidas diretamente.
Vamos enunciar o teorema e, em seguida, apresentar sua demonstração.
Observe a figura e uma possível proporção obtida pelo Teorema de Tales:
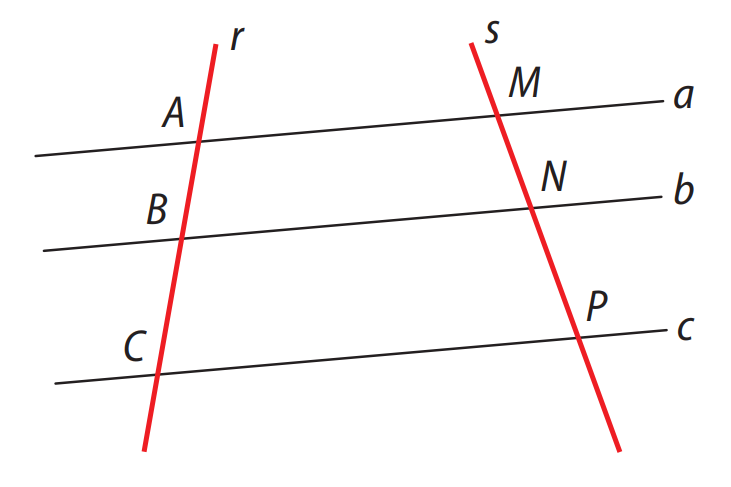
Figura: Segmentos determinados por transversais e retas paralelas
\( a \parallel b \parallel c \Rightarrow \frac{AB}{BC} = \frac{MN}{NP} \)
Com base nessa figura, podemos considerar outras proporções, como:
- \( \frac{AB}{AC} = \frac{MN}{MP} \)
- \( \frac{AC}{BC} = \frac{MP}{NP} \)
A partir da figura apresentada, quais outras proporções podem ser consideradas pelo teorema de Tales?
\( \frac{BC}{AB} = \frac{NP}{MN}, \quad \frac{BC}{MN} = \frac{AC}{MP}, \quad \frac{AC}{AB} = \frac{MP}{MN} \)
📚 Reforce seus estudos com materiais visuais e gratuitos
- 🧠 Mapa Mental de Geometria – Proporcionalidade e Tales
- 📘 Baixe agora os 10 eBooks de Matemática – É gratuito!
🔗 Leia também
Quer se aprofundar no tema? Confira o artigo completo:
👉 Feixe de Retas Paralelas
📌 Exercício Resolvido – Teorema de Tales
Enunciado:
A figura a seguir representa dois terrenos cujas laterais são paralelas. De acordo com a figura, determine as medidas de \( x \) e \( y \).
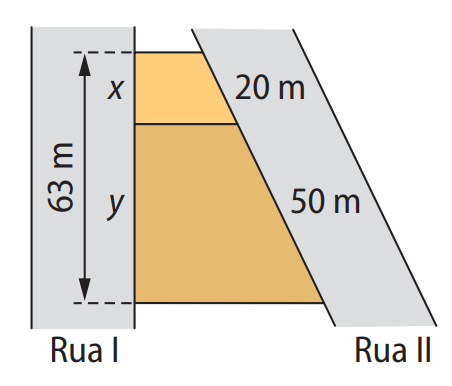
Resolução:
Pelo Teorema de Tales, temos:
\( \frac{20 + 50}{20} = \frac{x + y}{x} \quad \text{(I)} \)
\( \frac{20 + 50}{50} = \frac{x + y}{y} \quad \text{(II)} \)
Sabemos que \( x + y = 63 \). Substituindo esse valor na equação (I):
\( \frac{70}{20} = \frac{63}{x} \Rightarrow \frac{7}{2} = \frac{63}{x} \Rightarrow 7x = 126 \Rightarrow x = 18 \)
Agora, substituindo em (II):
\( \frac{70}{50} = \frac{63}{y} \Rightarrow \frac{7}{5} = \frac{63}{y} \Rightarrow 7y = 315 \Rightarrow y = 45 \)
Resposta final: As medidas são \( x = 18\, \text{m} \) e \( y = 45\, \text{m} \).
📌 Exercício Resolvido 2 – Teorema de Tales
Enunciado:
Na figura a seguir, \( a \parallel b \parallel c \). Determine a medida do segmento \( \overline{CD} \).
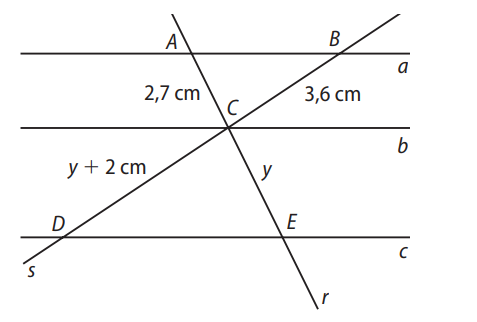
Resolução:
Aplicando o Teorema de Tales, temos:
\( \frac{2{,}7}{y} = \frac{3{,}6}{y + 2} \)
Multiplicando em cruz:
\( 2{,}7 \cdot (y + 2) = 3{,}6y \)
Distribuindo:
\( 2{,}7y + 5{,}4 = 3{,}6y \)
Isolando \( y \):
\( 5{,}4 = 3{,}6y – 2{,}7y = 0{,}9y \)
\( y = \frac{5{,}4}{0{,}9} = 6 \)
Portanto, a medida de \( \overline{CD} \) é:
\( CD = y + 2 = 6 + 2 = \boxed{8\,\text{cm}} \)













